算法提高课笔记（八）

1020. 潜水员（费用最低限度，掌握）

潜水员为了潜水要使用特殊的装备。
他有一个带2种气体的气缸：一个为氧气，一个为氮气。
让潜水员下潜的深度需要各种数量的氧和氮。
潜水员有一定数量的气缸。
每个气缸都有重量和气体容量。
潜水员为了完成他的工作需要特定数量的氧和氮。
他完成工作所需气缸的总重的最低限度的是多少？
例如：潜水员有5个气缸。每行三个数字为：氧，氮的（升）量和气缸的重量：
3 36 120
10 25 129
5 50 250
1 45 130
4 20 119
如果潜水员需要5升的氧和60升的氮则总重最小为249（1，2或者4，5号气缸）。
你的任务就是计算潜水员为了完成他的工作需要的气缸的重量的最低值。

输入格式
第一行有2个整数 m，n。它们表示氧，氮各自需要的量。
第二行为整数 k 表示气缸的个数。
此后的 k 行，每行包括ai，bi，ci，3个整数。这些各自是：第 i 个气缸里的氧和氮的容量及气缸重量。

输出格式
仅一行包含一个整数，为潜水员完成工作所需的气缸的重量总和的最低值。

数据范围
1≤m≤21,
1≤n≤79,
1≤k≤1000,
1≤ai≤21,
1≤bi≤79,
1≤ci≤800
输入样例：
5 60
5
3 36 120
10 25 129
5 50 250
1 45 130
4 20 119
输出样例：
249

二维费用背包的应用题。

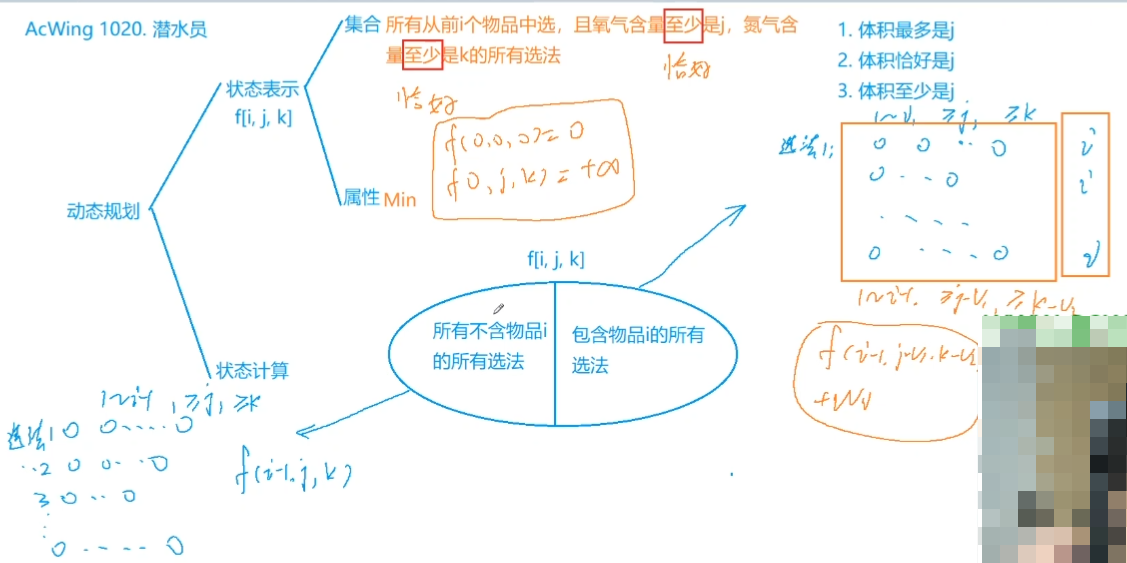
本题的费用限制与之前的题目不一样，要求的是最低限度，以前的费用限制大多是最高限度。

算是比较新颖的一个点，之前遇到的DP题都没有这种费用限制。

两种思路的具体分析参考文章： https://www.acwing.com/blog/content/458/。（很推荐看一下）

简单总结：

背包问题中的三种状态（针对求Min）

• 2.体积不超过v – 体积至多是v
  dp全部初始化为0，计算时严格保证任意状态下背包的体积 >= 0
• 1.体积恰好是v
  dp[0][0]初始化为0， 其他全部初始化为inf，同时也要严格保证任意状态下背包体积 >= 0
• 3.体积至少是v
  dp[0][0]初始化为0， 其他全部初始化为inf, 任意状态下背包的体积允许 < 0

当某个DP状态不合法时，求Min可以将其初始化为INF，或者初始化为-1，在转移时特判也行。

以前做的背包问题，都可以将状态表示的不超过改成恰好是，只需要把dp数组初始化修改就行。

注意：若题目求的是体积不超过v的最大值，若用体积恰好是v的状态表示需要枚举dp数组求最大值。

---

核心：在两维费用满足最低限度的情况下的总价值的最小值。

做法一（WA了）：状态表示，恰好为。

时间复杂度：O(n^2 * m^2)。

状态表示需要进行调整，将上一讲的二维费用模板题的状态表示由不超过改为恰好。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 22,M = 80;
int n,m,k;
int f[N*M][N*M];

int main(){
    cin >> n >> m >> k;
    
    memset(f,0x3f,sizeof f);
    f[0][0] = 0;
    
    int v1,v2,w;
    while (k--){
        cin >> v1 >> v2 >> w;
        for (int i = N*M-1;i >= v1;i --)
            for (int j = N*M-1;j >= v2;j --){
                f[i][j] = min(f[i][j],f[i-v1][j-v2] + w);
            }
    }
    
    int res = 1e9;
    for (int i = n;i < N*M;i ++)
        for (int j = m;j < N*M;j ++)
         res = min(res,f[i][j]);
    
    cout << res << '\n';
    return 0;
}
/* TLE，因为：极端情况下，需要枚举到f[n][n*m]，时间会炸
5 60
5
21 1 120
21 50 129
21 5 250
21 2 130
21 2 119
*/

题解二（正解）：状态表示，至少为。

状态表示需要进行调整，将上一讲的二维费用模板题的状态表示由不超过改为至少。

分析之后，发现代码好像和前面一模一样，到底哪里遗漏了？

问题在于转移方程f[i][j][k] = f[i-1][j-v1][k-v2]+w还是有区别的。

若表示为至少是，那么两个费用可以取成负数，也就是说f[i-1][j-v1][k-v2],j < v2,k < v2也是合法的状态；若表示为恰好是，那么费用一定是正数或零，不能取负数（不合法状态）。

当费用取成负数时，至少是一个负数，和至少是0在本题是等价的（价值大于等于1），所以通过负数转移就等价于通过0来转移。

就拿体积来说，至少需要多少体积，也就是说有体积比需要的体积大的物品还是能用得到，例如f[3][5]，至少需要3个体积，5个重量，求能拿到价值的最小值，现在只有一个物品，体积是4，重量是4，价值w，它说至少需要3个体积，那么体积是4还是可以用到，只是多了1个体积没用占着而已，不影响其价值。因此若用了这个物品，则变成了求f[-1][1] + w，也即至少还需要-1个体积和1个重量，至少需要-1个体积就说明体积已经达标甚至超过1个，表示体积已经不再需求了，只需要0个体积即可，等价于f[0][1] + w。

再次解释为什么会出现由费用为负数的状态进行状态转移的情况？

就拿做法一中的样例为例，目标是5和60，我们第一个选取21和50的气缸，显然费用1已经达标，此时状态的费用1就是负数了，但是费用2还没达标，还得选，就是说还要从当前的费用为负数的状态继续转移。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 25,M = 85;
int f[N][M];
int n,m,k;

int main(){
    cin >> n >> m >> k;
    
    memset(f,0x3f,sizeof f);
    f[0][0] = 0;
    
    int v1,v2,w;
    while (k--){
        cin >> v1 >> v2 >> w;
        for (int i = n;i >= 0;-- i)
            for (int j = m;j >= 0;-- j){ // 费用为负数的状态可以用费用为0的状态代替，避免越界
                f[i][j] = min(f[i][j],f[max(0,i-v1)][max(0,j-v2)] + w);
            }
    }
    
    cout << f[n][m] << '\n';
    return 0;
}

换一种角度描述，体积至少为V 等价于 还缺V个体积就达标了；如果给我V个体积再好不过了，实在没有给我V+1个体积也行。

278. 数字组合

给定 N 个正整数 A1,A2,…,AN，从中选出若干个数，使它们的和为 M，求有多少种选择方案。

输入格式
第一行包含两个整数 N 和 M。
第二行包含 N 个整数，表示 A1,A2,…,AN。

输出格式
包含一个整数，表示可选方案数。

数据范围
1≤N≤100,
1≤M≤10000,
1≤Ai≤1000,
答案保证在 int 范围内。

输入样例：
4 4
1 1 2 2
输出样例：
3

01背包求方案数的扩展。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10005;
int f[102][N];
int n,m;

int main(){
    cin >> n >> m;
    
    f[0][0] = 1; // 前0个物品，总体积恰好为0的方案数是1个，都不选
    // f[0][1] = f[0][2] = xxx = 0
    int x;
    for (int i = 1;i <= n;i ++){
        cin >> x;
        for (int j = 0;j <= m;j ++){
            f[i][j] = f[i-1][j]; // 不包含第i个物品的方案
            if (j >= x) f[i][j] += f[i-1][j-x]; // 包含第i个物品的方案
        }
    }
    
    cout << f[n][m] << '\n';
    return 0;
}

1019. 庆功会

为了庆贺班级在校运动会上取得全校第一名成绩，班主任决定开一场庆功会，为此拨款购买奖品犒劳运动员。
期望拨款金额能购买最大价值的奖品，可以补充他们的精力和体力。

输入格式：
第一行二个数n，m，其中n代表希望购买的奖品的种数，m表示拨款金额。
接下来n行，每行3个数，v、w、s，分别表示第I种奖品的价格、价值（价格与价值是不同的概念）和能购买的最大数量（买0件到s件均可）。

输出格式：
一行：一个数，表示此次购买能获得的最大的价值（注意！不是价格）。

数据范围
n≤500,m≤6000,
v≤100,w≤1000,s≤10

输入样例：
5 1000
80 20 4
40 50 9
30 50 7
40 30 6
20 20 1
输出样例：
1040

多重背包应用题。

朴素版多重背包时间复杂度：n*m*s = 3e7，可以过。

滚动数组的朴素多重背包问题。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 6005;
int f[N];
int n,m;

int main(){
    cin >> n >> m;
    
    int v,w,s;
    while (n -- ){
        cin >> v >> w >> s;
        for (int i = m;i >= 0;i --)
            for (int j = 0;j <= s && i >= j*v;j ++){
                f[i] = max(f[i],f[i-j*v] + j*w);
            }
    }
    
    cout << f[m] << '\n';
    return 0;
}