算法提高课笔记（七）

1024. 装箱问题

有一个箱子容量为 V，同时有 n 个物品，每个物品有一个体积（正整数）。
要求 n 个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。
    
输入格式
第一行是一个整数 V，表示箱子容量。
第二行是一个整数 n，表示物品数。
接下来 n 行，每行一个正整数（不超过10000），分别表示这 n 个物品的各自体积。

输出格式
一个整数，表示箱子剩余空间。

数据范围
0<V≤20000,
0<n≤30
输入样例：
24
6
8
3
12
7
9
7
输出样例：
0

题目很简单，01背包应用，价值也就是体积的值。

#include <iostream>
using namespace std;
const int N = 20005;
int f[N];

int main(){
    int v,n;
    cin >> v >> n;
    int x;
    for (int i = 1;i <= n;i ++){
        cin >> x;
        for (int j = v;j >= x;j --){
            f[j] = max(f[j],f[j-x] + x);
        }
    }
    cout << v - f[v] << '\n';
    return 0;
}

1022. 宠物小精灵之收服

宠物小精灵是一部讲述小智和他的搭档皮卡丘一起冒险的故事。
一天，小智和皮卡丘来到了小精灵狩猎场，里面有很多珍贵的野生宠物小精灵。
小智也想收服其中的一些小精灵。
然而，野生的小精灵并不那么容易被收服。
对于每一个野生小精灵而言，小智可能需要使用很多个精灵球才能收服它，而在收服过程中，野生小精灵也会对皮卡丘造成一定的伤害（从而减少皮卡丘的体力）。
当皮卡丘的体力小于等于0时，小智就必须结束狩猎（因为他需要给皮卡丘疗伤），而使得皮卡丘体力小于等于0的野生小精灵也不会被小智收服。
当小智的精灵球用完时，狩猎也宣告结束。
我们假设小智遇到野生小精灵时有两个选择：收服它，或者离开它。
如果小智选择了收服，那么一定会扔出能够收服该小精灵的精灵球，而皮卡丘也一定会受到相应的伤害；如果选择离开它，那么小智不会损失精灵球，皮卡丘也不会损失体力。
小智的目标有两个：主要目标是收服尽可能多的野生小精灵；如果可以收服的小精灵数量一样，小智希望皮卡丘受到的伤害越小（剩余体力越大），因为他们还要继续冒险。
现在已知小智的精灵球数量和皮卡丘的初始体力，已知每一个小精灵需要的用于收服的精灵球数目和它在被收服过程中会对皮卡丘造成的伤害数目。
请问，小智该如何选择收服哪些小精灵以达到他的目标呢？

输入格式
输入数据的第一行包含三个整数：N，M，K，分别代表小智的精灵球数量、皮卡丘初始的体力值、野生小精灵的数量。
之后的K行，每一行代表一个野生小精灵，包括两个整数：收服该小精灵需要的精灵球的数量，以及收服过程中对皮卡丘造成的伤害。

输出格式
输出为一行，包含两个整数：C，R，分别表示最多收服C个小精灵，以及收服C个小精灵时皮卡丘的剩余体力值最多为R。

数据范围
0<N≤1000,
0<M≤500,
0<K≤100
输入样例1：
10 100 5
7 10
2 40
2 50
1 20
4 20
输出样例1：
3 30
输入样例2：
10 100 5
8 110
12 10
20 10
5 200
1 110
输出样例2：
0 100

本题在01背包的基础上扩展，有两个目标：背包中尽可能多放物品；多放物品同时保证背包剩余空间最大。

本题属于二维费用背包，费用包括2个维度。

MLE代码：三维：一维物品数量 + 二维费用。

#include <iostream>
#include <algorithm>
using namespace std;
int n,m,k;
const int N = 1005,M = 505,K = 105;
int f[K][N][M]; // 空间约190MB，MLE

int main(){
    cin >> n >> m >> k;
    
    int x,y;
    for (int i = 1;i <= k;i ++){
        cin >> x >> y;
        for (int j = 0;j <= n;j ++)
            for (int t = 0;t <= m-1;t ++){// 体力上限应该是m-1，不能全消耗完
                f[i][j][t] = f[i-1][j][t];
                if (j-x>=0 && t-y>=0)
                    f[i][j][t] = max(f[i][j][t],f[i-1][j-x][t-y]+1);
            }
    }
    
    // 遍历求出满足收服最大精灵数量的最小体力
    int t = m-1; // 体力不能为0
    while (t > 0 && f[k][n][t-1] == f[k][n][m-1]) -- t;
    cout << f[k][n][m-1] << ' ' << m-t << '\n'; // 总体力减去最小需要体力就是消耗体力
    return 0;
}

AC代码：物品数量压缩。

#include <iostream>
#include <algorithm>
using namespace std;
int n,m,k;
const int N = 1005,M = 505;
int f[N][M];

int main(){
    cin >> n >> m >> k;
    
    int x,y;
    for (int i = 1;i <= k;i ++){
        cin >> x >> y;
        for (int j = n;j >= x;j --)
            for (int t = m-1;t - y >= 0;t --){// 体力上限应该是m-1，不能全消耗完
                f[j][t] = max(f[j][t],f[j-x][t-y]+1);
            }
    }
    
    // 遍历求出满足收服最大精灵数量的最小体力
    int t = m-1; // 体力不能为0
    while (t > 0 && f[n][t-1] == f[n][m-1]) -- t;
    cout << f[n][m-1] << ' ' << m-t << '\n'; // 总体力减去最小需要体力就是消耗体力
    return 0;
}

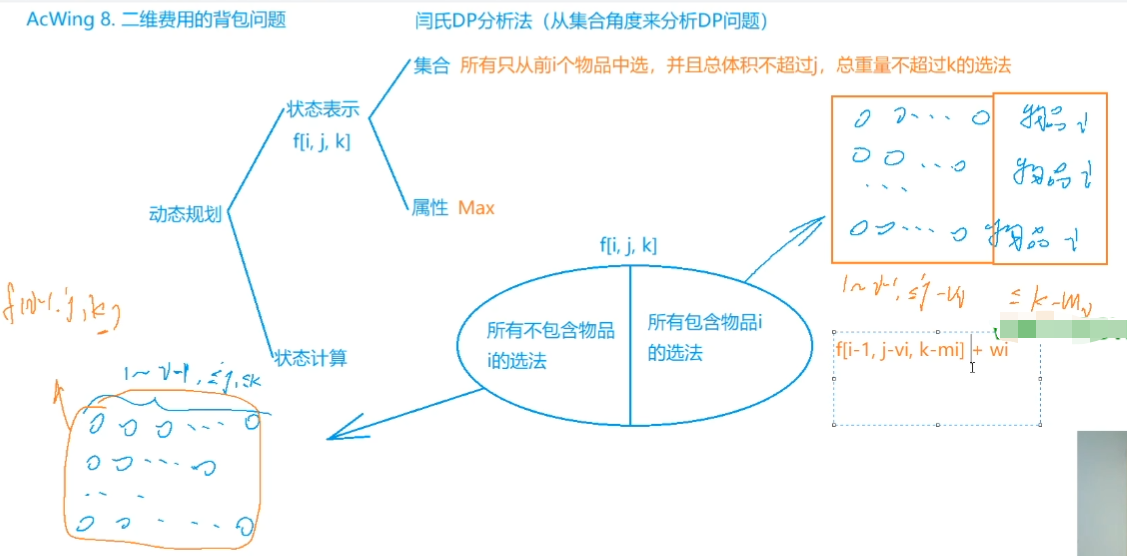
8. 二维费用的背包问题

有 N 件物品和一个容量是 V 的背包，背包能承受的最大重量是 M。
每件物品只能用一次。体积是 vi，重量是 mi，价值是 wi。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

输入格式
第一行三个整数，N,V,M，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有 N 行，每行三个整数 vi,mi,wi，用空格隔开，分别表示第 i 件物品的体积、重量和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N≤1000
0<V,M≤100
0<vi,mi≤100
0<wi≤1000
输入样例：
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6
输出样例：
8

从上一题抽象出来的模板题，本题将01背包问题和二维费用结合。

二维费用不仅可以和01背包问题结合，还可以和其他背包问题结合。

二维费用要求两个费用的要求同时满足达到最优解。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 105;
int f[N][N];
int n,v,m;

int main(){
    cin >> n >> v >> m;
    
    int x,y,z;
    for (int i = 1;i <= n;i ++){
        cin >> x >> y >> z;
        for (int j = v;j >= x;j --)
            for (int k = m;k >= y;k --){
                f[j][k] = max(f[j][k],f[j-x][k-y]+z);
            }
    }
    cout << f[v][m] << '\n';
    return 0;
}