1023. 买书
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| 小明手里有n元钱全部用来买书,书的价格为10元,20元,50元,100元。
问小明有多少种买书方案?(每种书可购买多本)
输入格式
一个整数 n,代表总共钱数。
输出格式
一个整数,代表选择方案种数。
数据范围
0≤n≤1000
输入样例1:
20
输出样例1:
2
输入样例2:
15
输出样例2:
0
输入样例3:
0
输出样例3:
1
|
完全背包问题应用题,求方案数。
状态表示应该是前i个物品,总价恰好为j的方案数。
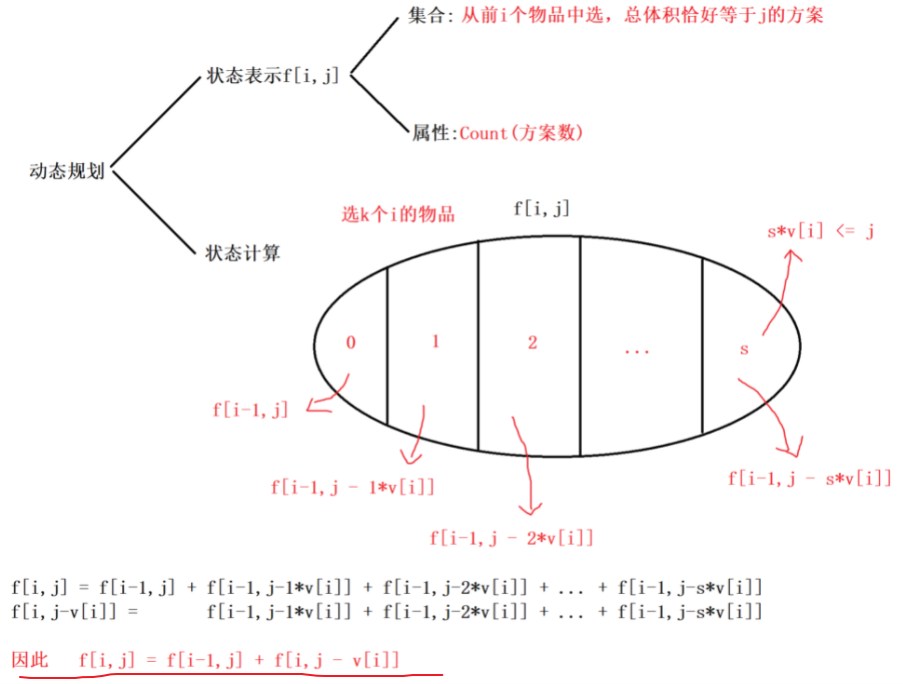
题解一:二维DP。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include <iostream>
#include <algorithm>
using namespace std;
const int N = 1005;
int v[5] = {0,10,20,50,100};
int f[5][N];
int n;
int main(){
cin >> n;
f[0][0] = 1;
for (int i = 1;i <= 4;i ++)
for (int j = 0;j <= n;j ++){
f[i][j] = f[i-1][j];
if (j >= v[i]) f[i][j] += f[i][j-v[i]];
}
cout << f[4][n] << '\n';
return 0;
}
|
题解二:一维DP。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| #include <iostream>
#include <algorithm>
using namespace std;
const int N = 1005;
int v[5] = {0,10,20,50,100};
int f[N];
int n;
int main(){
cin >> n;
f[0] = 1;
for (int i = 1;i <= 4;i ++)
for (int j = v[i];j <= n;j ++){
f[j] += f[j-v[i]];
}
cout << f[n] << '\n';
return 0;
}
|
12. 背包问题求具体方案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| 有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 字典序最小的方案。这里的字典序是指:所选物品的编号所构成的序列。物品的编号范围是 1…N。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一行,包含若干个用空格隔开的整数,表示最优解中所选物品的编号序列,且该编号序列的字典序最小。
物品编号范围是 1…N。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例:
1 4
|
来自背包九讲。思路有难度。
之前的背包问题求解都只需要求出最优方案的价值,实际上也可以求出具体的方案。
类比最短路问题,不仅可以求出最短路的长度,还可以求最短路的路径。这就是之前提到的DP和最短路的关系,参考这篇拓扑图的题解: https://www.acwing.com/solution/content/53963/。
本题是求01背包的具体方案,其他背包问题做法类似。
题解一:DP路径倒推。
思路:
求最优方案,也就是最优方案的转移路径,需要判断每个物品选了还是没选。
- 我们要先通过一遍二维DP求出最优方案的价值,这样每个
f[i][j]都是最优解。
- 再遍历每个物品看看是否要选择从而求出最优方案。
由于题目要求求字典序最小的方案,因此从1到n中,每个物品有3种情况:
(1)只能选,则必须选;
(2)不能选,则必不选;
(3)可选可不选,则必须选;这说明后面也存在至少一个物品和当前物品二选一,选前者满足字典序最小。
为了满足字典序最小的要求,我们第一步必须倒序遍历求最优方案的价值。
为什么要倒序求最优方案的价值呢?
因为第一步和第二步的遍历顺序必须是相反的,从起点走到终点,再倒推回去找到最短路。
对于第i个物品是否要选(出现在最优方案中),
需要判断f[i][j] 与 f[i-1][j]和f[i-1][j-v[i]] + w[i]的大小关系。
也就对应上面的每个物品的三种情况,当f[i][j]等于前者,必不选;当等于后者,必选;当等于前者和后者,必须选。
第二步判断物品是否可选是正向遍历的,必须保证f[1][m]就是最优方案的价值,这样第二步通过f[1][m]才能判断是否选第一个物品,然后是第二个,第三个,…
如果第一步正向遍历,那么f[1][m]只考虑了第一个物品在体积不超过m情况下的最优方案的价值,而第二步开始遍历f[1][m]时它应该表示从第1到n个物品在体积不超过m情况下的最优方案的价值,两者就对应不上。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| import java.io.*;
public class Main{
static int N = 1010;
static int[][] f = new int[N][N];
static int[] v = new int[N];
static int[] w = new int[N];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n,m;
String[] str = br.readLine().split(" ");
n = Integer.parseInt(str[0]);
m = Integer.parseInt(str[1]);
for (int i = 1;i <= n;i ++){
str = br.readLine().split(" ");
v[i] = Integer.parseInt(str[0]);
w[i] = Integer.parseInt(str[1]);
}
br.close();
for (int i = n;i >= 1;i --){
for (int j = 0;j <= m;j ++){
f[i][j] = f[i+1][j];
if (j >= v[i]) f[i][j] = Math.max(f[i][j],f[i+1][j-v[i]] + w[i]);
}
}
int j = m;
for (int i = 1;i <= n;i ++){
if (j >= v[i] && f[i][j] == f[i+1][j-v[i]] + w[i]){
System.out.print(i + " ");
j -= v[i];
}
}
}
}
|
题解二:g数组记录最优方案。
受这个题解启发: https://www.acwing.com/solution/content/51015/。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| import java.io.*;
public class Main {
static int N = 1010;
static int[][] f = new int[N][N];
static boolean[][] g = new boolean[N][N];
static int[] v = new int[N];
static int[] w = new int[N];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n,m;
String[] str = br.readLine().split(" ");
n = Integer.parseInt(str[0]);
m = Integer.parseInt(str[1]);
for (int i = 1;i <= n;i ++){
str = br.readLine().split(" ");
v[i] = Integer.parseInt(str[0]);
w[i] = Integer.parseInt(str[1]);
}
br.close();
for (int i = n;i >= 1;i --){
for (int j = 0;j <= m;j ++){
f[i][j] = f[i+1][j];
g[i][j] = false;
if (j >= v[i] && f[i][j] <= f[i+1][j-v[i]] + w[i]){
g[i][j] = true;
f[i][j] = f[i+1][j-v[i]] + w[i];
}
}
}
int j = m;
for (int i = 1;i <= n;i ++) {
if (g[i][j]) {
j -= v[i];
System.out.print(i + " ");
}
}
}
}
|
题解三:递归写法。
参考题解: https://www.acwing.com/solution/content/19760/。


