1013. 机器分配
总公司拥有M台 相同 的高效设备,准备分给下属的N个分公司。
各分公司若获得这些设备,可以为国家提供一定的盈利。盈利与分配的设备数量有关。
问:如何分配这M台设备才能使国家得到的盈利最大?
求出最大盈利值。
分配原则:每个公司有权获得任意数目的设备,但总台数不超过设备数M。
输入格式
第一行有两个数,第一个数是分公司数N,第二个数是设备台数M;
接下来是一个N*M的矩阵,矩阵中的第 i 行第 j 列的整数表示第 i 个公司分配 j 台机器时的盈利。
输出格式
第一行输出最大盈利值;
接下N行,每行有2个数,即分公司编号和该分公司获得设备台数。
答案不唯一,输出任意合法方案即可。
数据范围
1≤N≤10,
1≤M≤15
输入样例:
1
2
3
4
| 3 3
30 40 50
20 30 50
20 25 30
|
输出样例:
本题是分组背包和背包求具体方案的结合题。
抽象出分组背包模型:
每个分公司就是一个物品组,每个物品组总共有m+1种选择(仅且仅能做出一种选择),可以选择0,1,2,…,m台机器,也就对应相应数量的体积。
回顾一下分组背包。
f[i][j]的状态表示就是前i组物品总体积不超过j的最优方案的价值。
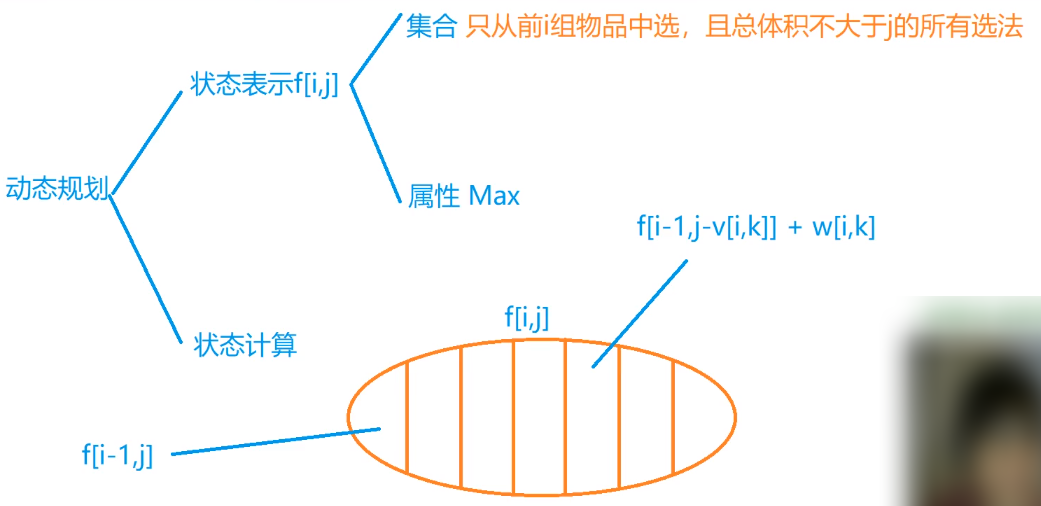
题目又要求输出方案,所以还要结合背包求具体方案。
题目没有要求字典序,所以可以先正向遍历,再反向遍历。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include <iostream>
#include <algorithm>
using namespace std;
const int N = 12,M = 17;
int f[N][M];
int w[N][M];
int way[N];
int n,m;
int main(){
cin >> n >> m;
for (int i = 1;i <= n;i ++)
for (int j = 1;j <= m;j ++) cin >> w[i][j];
for (int i = 1;i <= n;i ++)
for (int j = 0;j <= m;j ++){
f[i][j] = f[i-1][j];
for (int k = 1;k <= j;k ++)
f[i][j] = max(f[i][j],f[i-1][j-k]+w[i][k]);
}
cout << f[n][m] << '\n';
int j = m;
for (int i = n;i >= 1;i --)
for (int k = 0;k <= j;k ++){
if (f[i][j] == f[i-1][j-k]+w[i][k]){
way[i] = k;
j -= k;
break;
}
}
for (int i = 1;i <= n;i ++)
cout << i << " " <<way[i] << '\n';
return 0;
}
|
11. 背包问题求方案数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| 有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 最优选法的方案数。注意答案可能很大,请输出答案模 10^9+7 的结果。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示 方案数 模 10^9+7 的结果。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例:
2
|
来自背包九讲。


