考研算法辅导课笔记（六）

1.第五讲 二叉排序树、表达式树

先回顾一下上一讲的几道真题。

真题讲解

2015-2

先序序列为a,b,c,d的不同二叉树的个数是 （）？

解法一：直接根据先序序列推测可能的二叉树。

首先a肯定是根，然后b,c,d是左右子树，将它们分成两半有：0,3 ; 1,2 ; 2,1 ; 3,0四大种分法，然后在递归划分，最后加起来是14种。

解法二：考虑总节点数为4的不同二叉树的个数。

套用公式，节点数为n的不同二叉树的个数就是：

卡特兰数： $\frac {\binom{2n}{n}} {n+1}$. 代入n = 4得到14。（前面介绍n个元素的出栈顺序也是卡特兰数）

2016-42

（1）

解法一：数学归纳法，如图。

解法二：利用树的重要性质：节点数 = 边数 + 1，建立方程直接计算，如图。

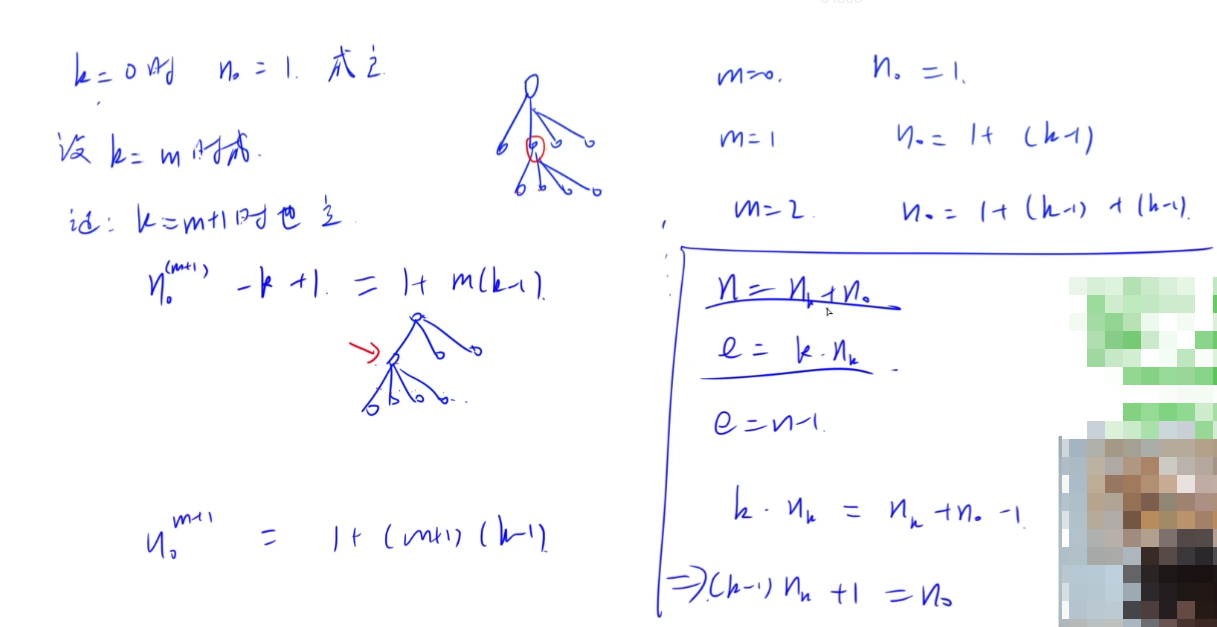
（2）很容易想到。

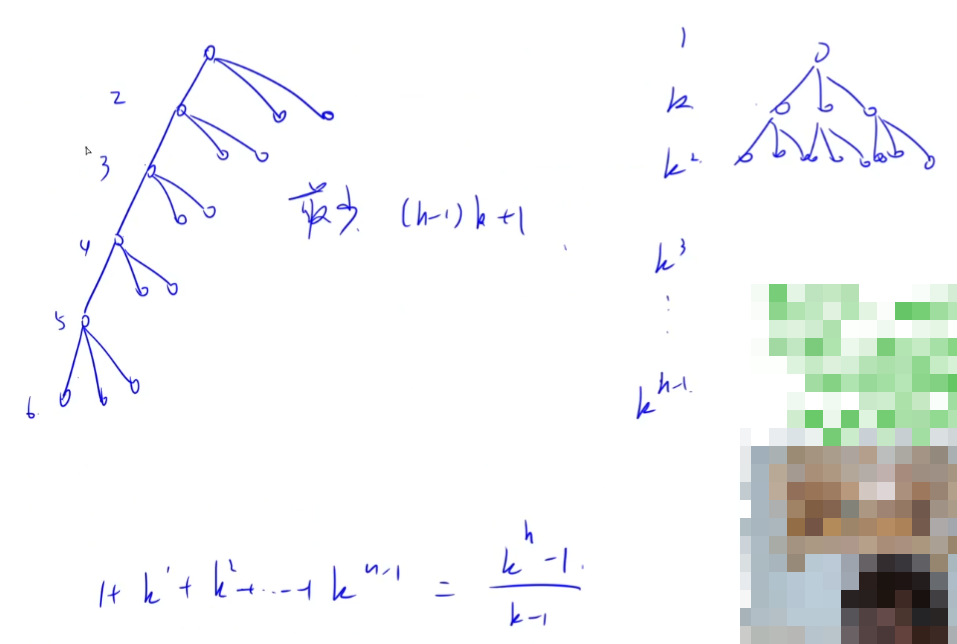
2020-3（不会）

解答：题目给出的节点数没用，考虑最坏情况，所有节点都只有右子树，需要2^5 - 1个存储单元。

知识点

1. 二叉排序树
2. 平衡树——AVL
   (1) 定义：满足如下条件的树：

    a. 是二叉查找树
    b. 每个节点的左子树和右子树的高度差最多为1
   

   (2) 平衡因子：一个结点的左子树的高度减去右子树的高度，可取-1、0、1三种值
   (3) 平衡操作
3. 表达式树

---

详细了解BST和AVL基本操作及其代码可以参考《算法笔记》P310.

二叉排序树要求掌握代码，平衡树AVL不要求掌握代码，只要学会思想。（平衡树代码参考提高课和进阶课）

二叉排序树—BST

注：二叉排序树，又称为二叉搜索树，二叉查找树（BST）。

BST 简介： https://oi-wiki.org/ds/bst/

二叉搜索树是一种二叉树的树形数据结构，其定义如下：

1. 空树是二叉搜索树。
2. 若二叉搜索树的左子树不为空，则其左子树上所有点的附加权值均小于其根节点的值。
3. 若二叉搜索树的右子树不为空，则其右子树上所有点的附加权值均大于其根节点的值。
4. 二叉搜索树的左右子树均为二叉搜索树。

对BST进行中序遍历，可以得到一个递增的有序序列。

判断一棵树是二叉搜索树：1.定义，每个节点都满足：左子树所有点 < 根 < 右子树所有点；2.中序序列有序。

BST本质上就是动态维护一个中序序列。

如果BST中每个点的值都不相等，那么定义相同；如果BST中存在值相等的两个不同点，有多种定义方式，可以放左边，也可以放右边，不影响本质。

从BST的定义上发现它和堆特别像，但两者是有区别的。

二叉排序树和堆的区别：

1. 结构上：BST，左子树 < 根 < 右子树；Heap（小根堆），根 < 左右子树，但是左右子树没有大小之分。
2. 作用上：二叉排序树是用来做查找的，而堆是用来做排序的。

BST的基本操作：

二叉搜索树上的基本操作所花费的时间与这棵树的高度成正比。

基本操作包括：插入，删除，查找，都是一条路往下走，时间复杂度：O(h) 。

插入：

根据要插入的值x，若 x 小于根的值，插入左子树；若 x 大于根的值，插入右子树。

要插入的位置一定是一个叶节点的左子树或者右子树。

删除：

按要删除节点 n 的 种类分为三种情况：

1. 叶子节点，直接删除，不影响；
2. 只有左子树或右子树的节点，删除节点，并将子树上移；
3. 同时有左子树和右子树的节点，用 n 的直接后继（或直接前驱）替代 n ，然后删掉这个直接后继（或直接前驱），递归到最后转化为情况1和2。（y总用的直接前驱，王道用的直接后继，都可以）

每次删除操作一定存在三种情况：

待删除的结点只有左子树。立即可推出，左子树上的结点都是小于待删除的结点的，我们只需要把待删除结点删了然后左子树接上待删除结点的父节点就可以了。
待删除的结点只有右子树。立即可推出，右子树上的结点都是大于待删除的结点的，我们只需要把待删除结点删了然后右子树接上待删除结点的父节点就可以了。
待删除的结点既有左子树又有右子树。这个比上两个情况麻烦一点，但也不麻烦，需要读者理解的是，怎么能删除结点后还不改变中序遍历的结果，并且操作代价最小，显而易见，我们根据待删除结点的左子树可以得到最右下角的最后结点满足 <x 并且最接近x的结点，把这个结点覆盖待删除的结点，然后把这个结点删除，就完成了我们的操作。

查找：

递归查找，类似二分。

平衡二叉树—AVL

一般的二叉查找树在极端情况下会退化成一个单链表，所以引入平衡树。

平衡二叉搜索树，简称为BBST。

参考讲解视频： 邓俊辉P253.（不懂的话还可以看看王道视频）

平衡树BT包括1.红黑树 2.AVL树 3.SBT 4.Treap 5.伸展树 等等。

AVL 树，是一种平衡的二叉搜索树。

满足如下条件的树：
a. 是二叉查找树（BST）；
b. 每个节点的左子树和右子树的高度差最多为1。

平衡因子：一个结点的左子树的高度减去右子树的高度，可取-1、0、1三种值

最小不平衡子树：指离插入节点最近且以平衡因子的绝对值大于1的节点作为根的子树。

从插入节点往上，找到的最近的不平衡的节点就是最小不平衡子树的根。

平衡树高度：O(log n)

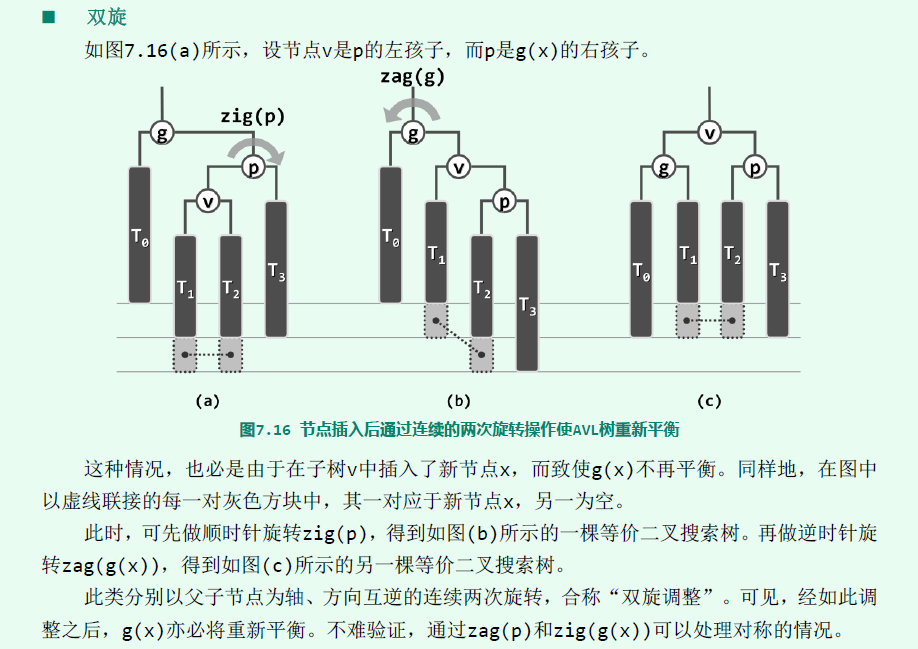
平衡操作：（为了处理插入，删除操作导致的失衡现象）

插入一个节点只会导致它的所有祖先可能失衡，其他节点不受影响。

删除一个节点只会导致它的父亲可能失衡，其他节点不受影响。

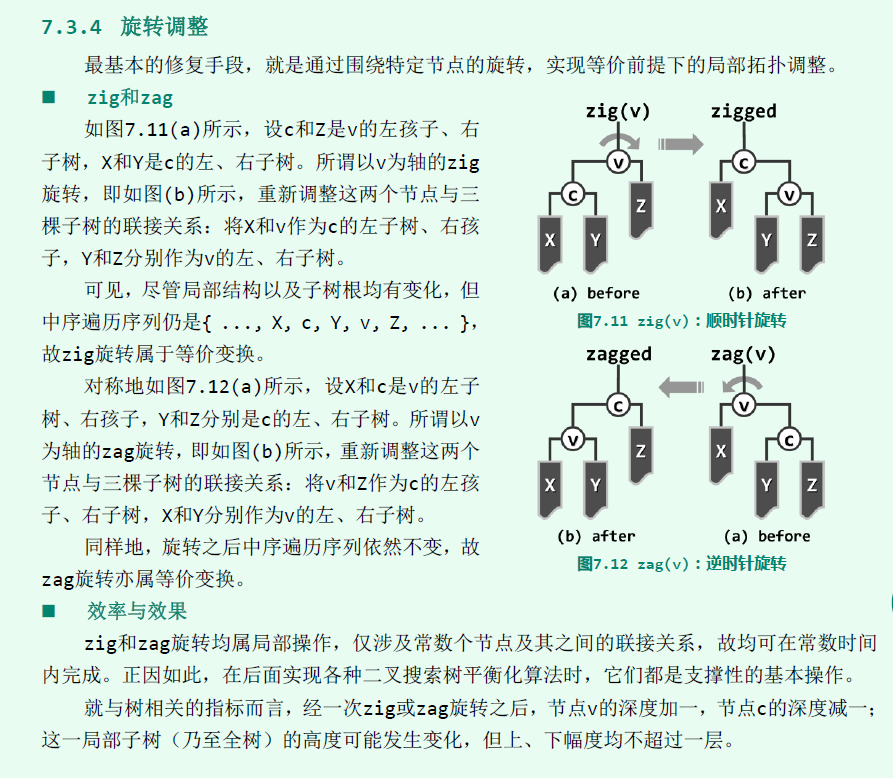
旋转操作不改变BT的中序遍历；

左旋与右旋是对称的操作；

上图中得到：

顺时针旋转（zig）对应右旋（right rotation），逆时针旋转（zag）对应左旋（left rotation）。

这个单旋转过程可以形象化记忆。

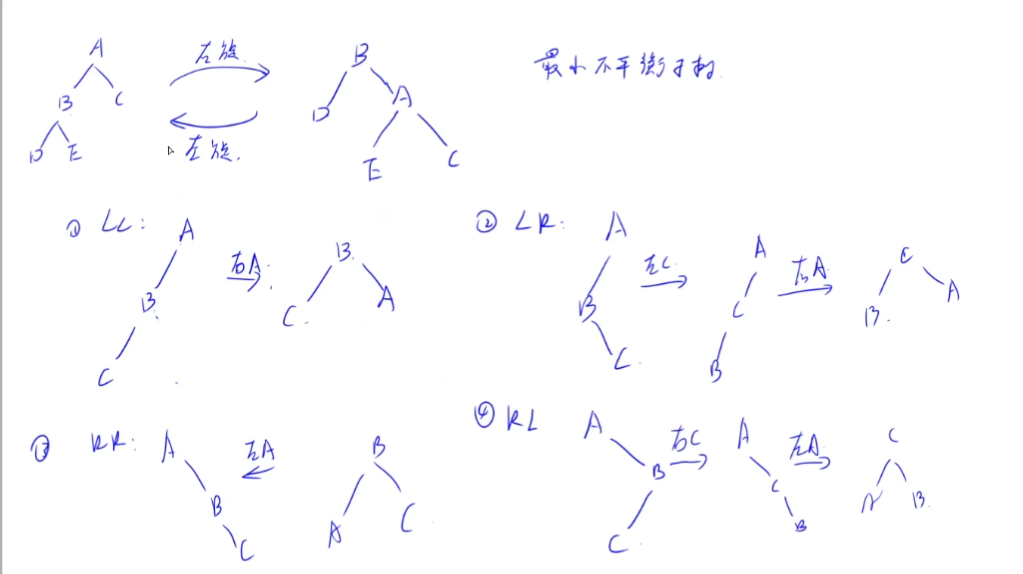
插入节点的单旋与双旋：

其中单旋还可以分为：LL平衡旋转（左单旋），RR平衡旋转（右单旋）；

其中双旋还可以分为：LR平衡旋转（先左后右双旋），RL平衡旋转（先右后左双旋）。

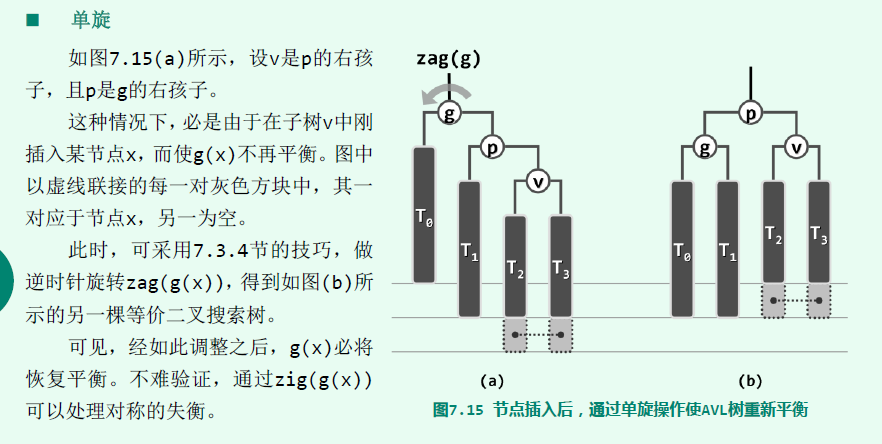
最后看看y总的总结：（必须掌握如何旋转，往哪个方向旋转，但不用深究为什么这样做能重平衡）

acwing.3786. 二叉排序树

你需要写一种数据结构，来维护一些数，其中需要提供以下操作：
插入数值 x。
删除数值 x。
输出数值 x 的前驱(前驱定义为现有所有数中小于 x 的最大的数)。
输出数值 x 的后继(后继定义为现有所有数中大于 x 的最小的数)。
题目保证：
操作 1 插入的数值各不相同。
操作 2 删除的数值一定存在。
操作 3 和 4 的结果一定存在。
    
输入格式
第一行包含整数 n，表示共有 n 个操作命令。
接下来 n 行，每行包含两个整数 opt 和 x，表示操作序号和操作数值。

输出格式
对于操作 3,4，每行输出一个操作结果。

数据范围
1≤n≤2000，
−10000≤x≤10000
输入样例：
6
1 1
1 3
1 5
3 4
2 3
4 2
输出样例：
3
5

参考题解： https://www.acwing.com/solution/content/55445/

思路：

插入和删除前面已经介绍。

查找：

如何找到数值 x 的前驱节点：

递归搜索至当前节点，设它的值为val。

if val >= x : 递归左子树;
else : return max{val,递归右子树};

如何找到数值 x 的后继节点：

只要将 <= 改成 >= ， max 改成 min ，左右子树交换就行。

#include <iostream>
#include <algorithm>
using namespace std;
const int INF = 1e6;

struct TreeNode{
    int val;
    TreeNode *left,*right;
    
    TreeNode(int x) : val(x),left(NULL),right(NULL){}
}*root;

void insert(TreeNode *&root,int x){
    if (!root) root = new TreeNode(x); // 找到一个空的位置插入新元素
    else if (root->val > x) insert(root->left,x);
    else insert(root->right,x);
}

void remove(TreeNode *&root,int x){
    if (!root) return; // 最终搜索到叶子说明找不到x
    else if (root->val > x) remove(root->left,x);
    else if (root->val < x) remove(root->right,x);
    else{ // 找到了，root对应的就是x所在节点，分三种情况
        // 叶子直接删掉
        if (!root->left && !root->right) root = NULL;
        // 只有一棵子树，直接把子树提上来
        else if (!root->left) root = root->right;
        else if (!root->right) root = root->left;
        else{
            // 找到x的直接前驱，将值复制给root覆盖x，然后删掉前驱
            auto t = root->left;
            while (t->right) t = t->right;
            root->val = t->val;
            remove(root->left,t->val);
        }
    }
}

int get_pre(TreeNode *root,int x){
    if (!root) return -INF; // 当x没有直接前驱时返回-INF
    // 当 root->val >= x 时，说明root及它的右子树不可能找到x的前驱
    else if (root->val >= x) return get_pre(root->left,x);
    // 当 root->val < x 时，说明root及它的右子树可能找到x的前驱
    else return max(root->val,get_pre(root->right,x));
}

int get_suc(TreeNode *root,int x){
    if (!root) return INF;// 当x没有直接后继时返回INF
    else if (root->val <= x) return get_suc(root->right,x);
    else return min(root->val,get_suc(root->left,x));
}

int main(){
    int n;
    cin >> n;
    
    int op,x;
    while (n--){
        cin >> op >> x;
        if (op == 1) insert(root,x);
        else if (op == 2) remove(root,x);
        else if (op == 3) cout << get_pre(root,x) << '\n';
        else cout << get_suc(root,x) << '\n';
    }
    return 0;
}