grant's Blog

记录生活中的点点滴滴

考研算法辅导课笔记（七）

发表于 更新于 分类于 ， ，   阅读次数： Valine：
本文字数： 5.9k 阅读时长 ≈ 5 分钟

真题讲解

2013-3

image-20211202105740224

解答：

image-20211202110430569

答案是：3。

王道教材P178还有个例题，涉及单旋和双旋，可以做一下。

2011-7

image-20211202133525042

解答：

按照选项给定序列构建一棵二叉排序树，看看中序序列是否有序，如果有序说明合法。

A选项的中序序列不是递增的，无序，选A。

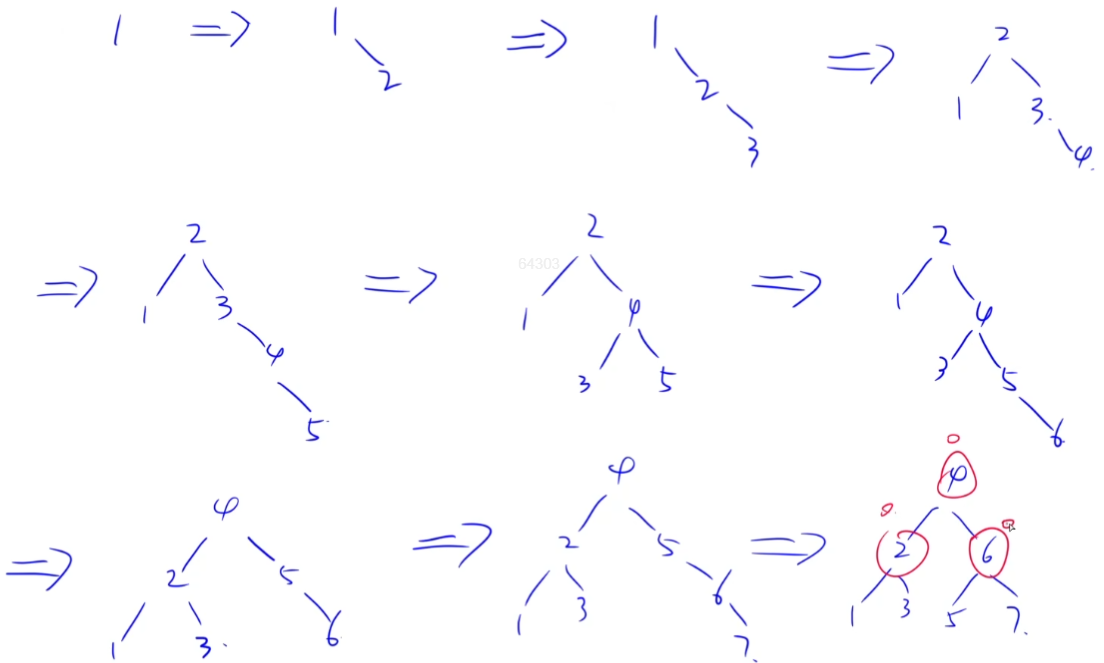
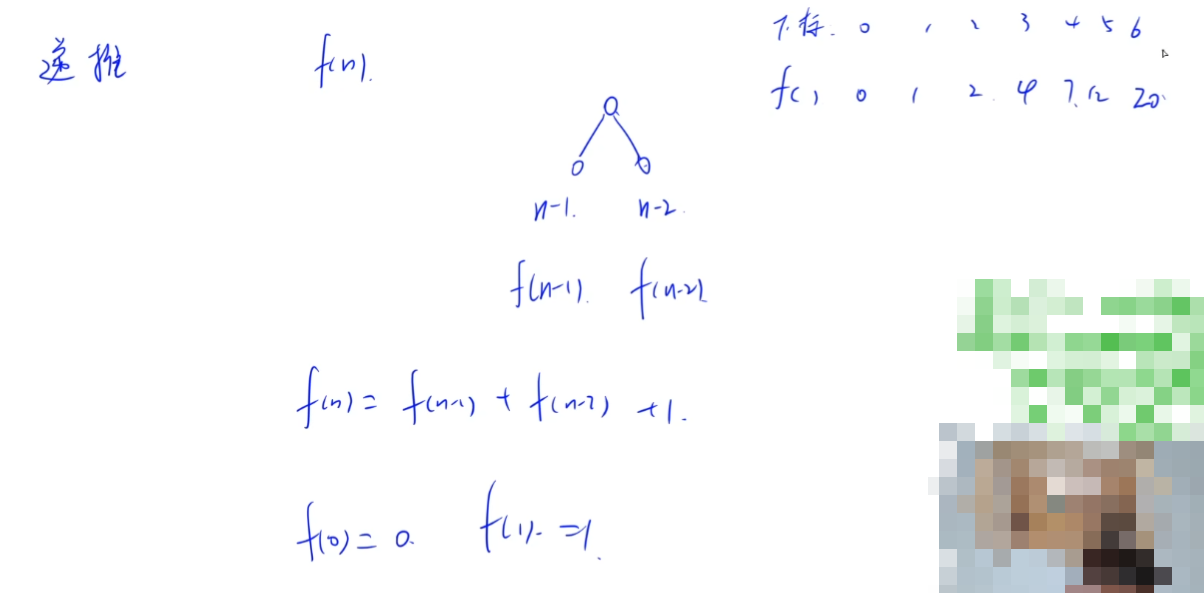
2012-4（有难度）

image-20211202135143931

解答：递推解决，这里算是AVL的补充知识点，就是一个类斐波那契数列。

image-20211202135725930

所以选B。

2013-6

image-20211202135934121

解答：选择C。

叶子节点删除再加回来一定会找到原来的位置插入，所以前后相同。

非叶子节点可以模拟一下，删掉之后它的位置被直接前驱顶替，再加回来肯定不一样。

因为插入是找空位插入，不会改变原有结构，而删除可能改变原有结构。

2015-4

image-20211202140801479

解答：一般的AVL树的中序序列一定是升序序列，题目说可得到降序序列说明它定义的AVL树是相反的。

A，B，C都可以举出反例，D是对的。最大元素如果有左子树，又因为左子树元素都比它大，所以矛盾。

2019-4（有难度）

image-20211202142206300

解答：

模拟一下叶子节点的情况。

image-20211202142416971

模拟一下非叶子节点的情况。

image-20211202142740152

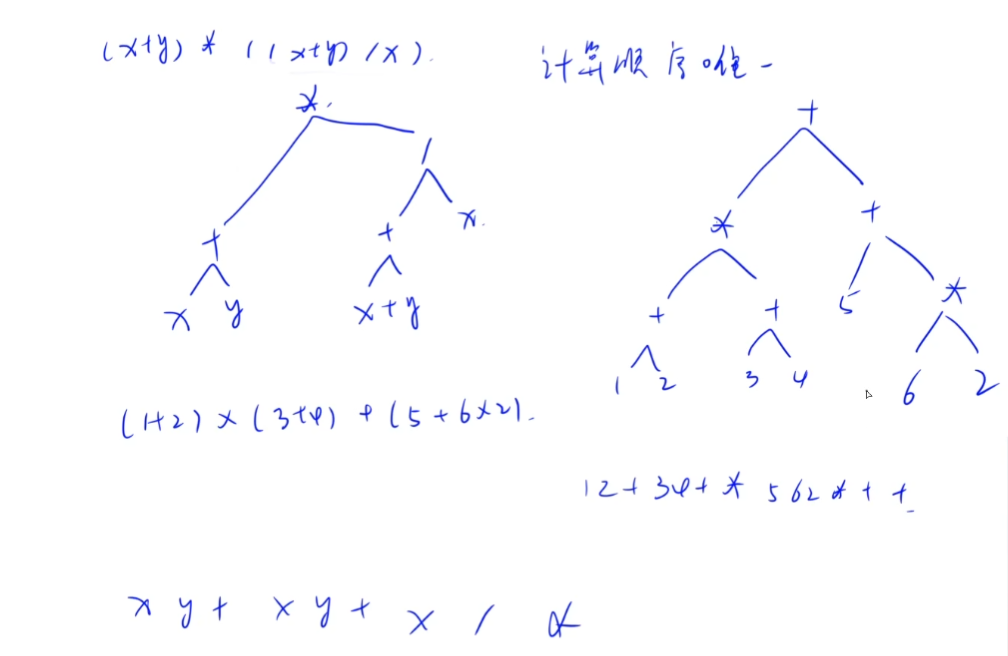
表达式树

一个表达式序列对应着一棵表达式树。

表达式树（二叉树）的前，中，后序遍历就是前，中，后缀表达式。

对应王道教材的有向无环图描述表达式P231,232。

image-20211202112653942

对与上图左边的树，用有向无环图描述可以省略重复节点，只需要 5 个节点。

image-20211202133258662

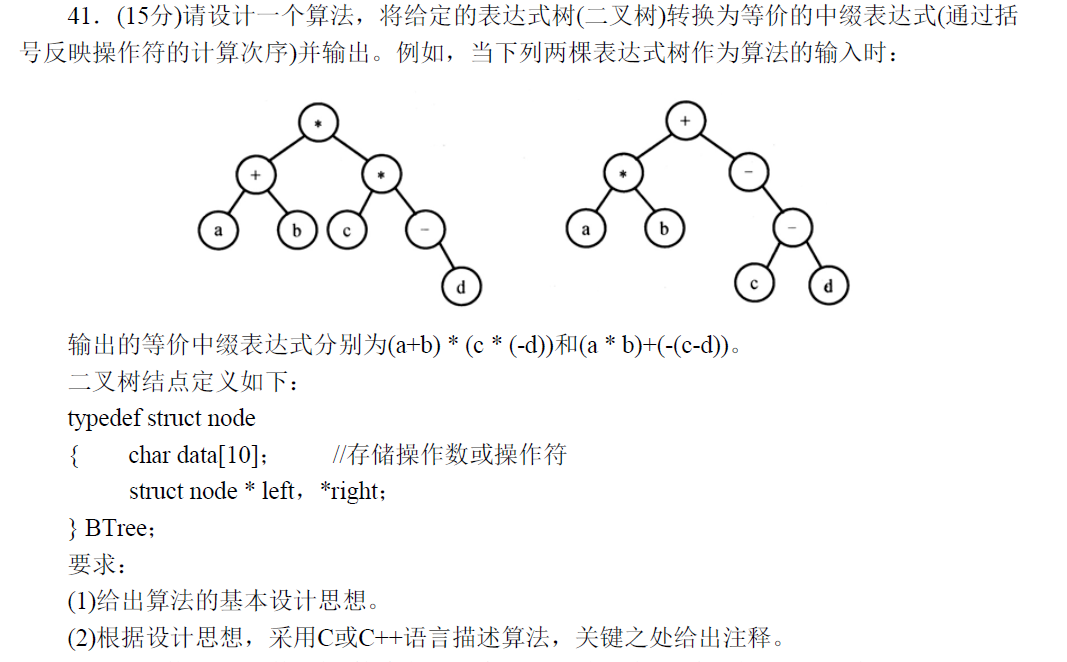
2017-41

image-20211203165823561

acwing.3765. 表达式树

请设计一个算法，将给定的表达式树(二叉树)转换为等价的中缀表达式(通过括号反映操作符的计算次序)并输出。

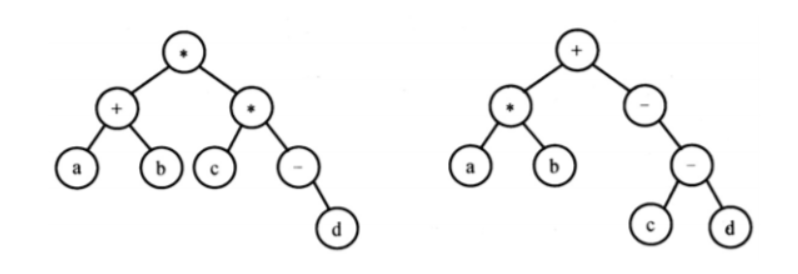
例如，当下列两棵表达式树作为算法的输入时：

image-20211203170056005

输出的等价中缀表达式分别为 (a+b)*(c*(-d)) 和 (a*b)+(-(c-d))。

注意：

  • 树中至少包含一个运算符。
  • 当运算符是负号时，左儿子为空，右儿子为需要取反的表达式。
  • 树中所有叶节点的值均为非负整数。

样例：

1
2
3
4
5
6
7
8
输入：二叉树[+, 12, *, null, null, 6, 4, null, null, null, null]如下图所示：
    +
   / \
  12  *
     / \
    6   4

输出：12+(6*4)

数据范围

给定二叉树的非空结点数量保证不超过 1000。

给定二叉树保证能够转化为合法的中缀表达式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     string val；
 *     TreeNode *left;
 *     TreeNode *right;
 * };
 */
class Solution {
public:
    string dfs(TreeNode *root){
        if (!root) return ""; // 空节点返回空
        if (!root->left && !root->right) return root->val; // 叶子节点返回根的值
        return "(" + dfs(root->left) + root->val + dfs(root->right) + ")";
    }

    string expressionTree(TreeNode* root) {
        return dfs(root->left) + root->val + dfs(root->right);
    }
};
// 上面代码的实际时间复杂度是：O(n^2)，返回string时会拷贝一份返回
// 改成下面的，时间复杂度降为：O(n)
class Solution {
public:
    string ans;
    
    void dfs(TreeNode *root){
        if (!root) return; // 空节点返回空
        if (!root->left && !root->right){
            ans += root->val; // 叶子节点返回根的值
            return;
        }
        ans += "(" ;
        dfs(root->left);
        ans += root->val;
        dfs(root->right);
        ans += ")";
    }

    string expressionTree(TreeNode* root) {
        dfs(root->left), ans += root->val, dfs(root->right);
        return ans;
    }
};

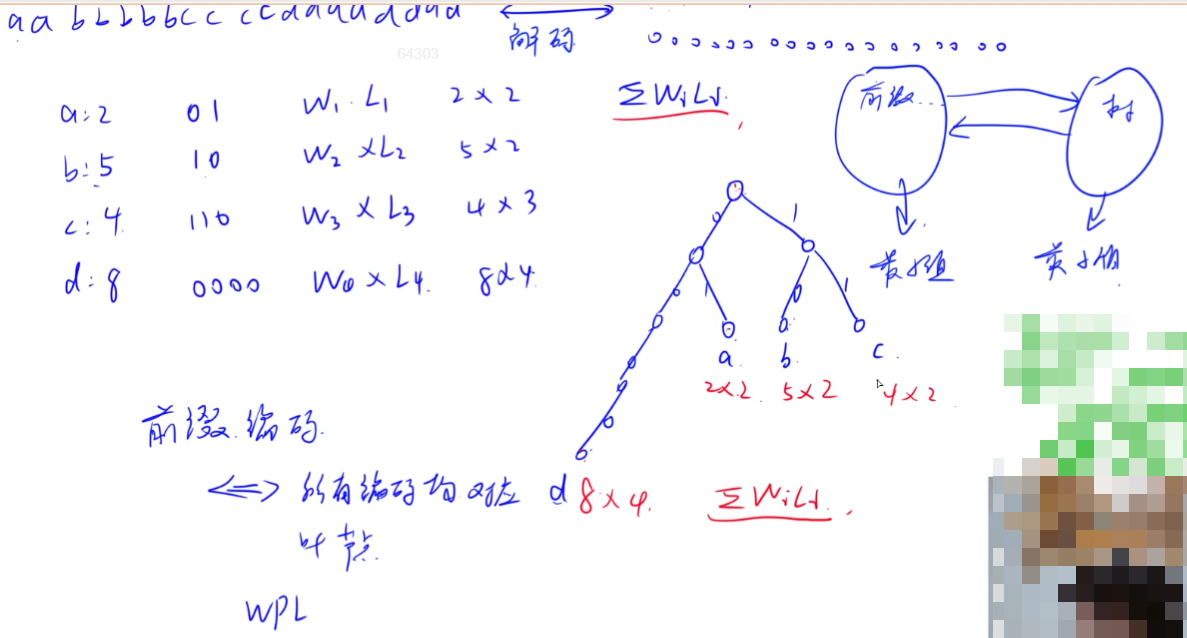
第六讲 Huffman编码和Huffman树

考察重点，历年常考。

(1) Huffman编码

  • a. 前缀编码: 是指对字符集进行编码时，要求字符集中任一字符的编码都不是其它字符的编码的前缀。
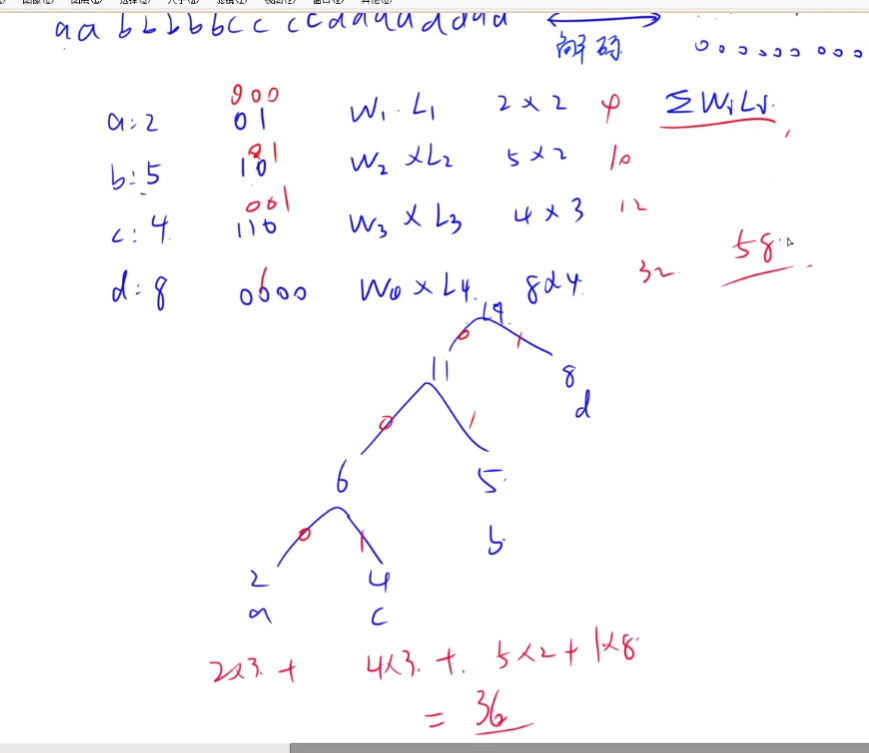
  • b. 树的带权路径长度(WPL)
  • c. 构造过程

(2) Huffman树

(3) 应用

Huffman编码采用前缀编码的方式，任一字符的编码都不是其它字符的编码的前缀。

所以编码过程和解码过程是一一对应的。

下图是一种一般的编码方式。

image-20211203194550851

下面介绍哈夫曼编码，使得句子总长度尽可能小（WPL尽可能小）。

算法进阶指南P86讲解了哈夫曼树。

哈夫曼树也称为最佳归并树。（可以由二路归并拓展到k-路归并）

最佳归并也就是最小代价的归并策略。

构造过程很容易的。

image-20211203195733798

acwing.148.合并果子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
在一个果园里，达达已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。
达达决定把所有的果子合成一堆。
每一次合并，达达可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。

可以看出，所有的果子经过 n−1 次合并之后，就只剩下一堆了。
达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家，所以达达在合并果子时要尽可能地节省体力。

假定每个果子重量都为 1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使达达耗费的体力最少，并输出这个最小的体力耗费值。
    
例如有 3 种果子，数目依次为 1，2，9。
可以先将 1、2 堆合并，新堆数目为 3，耗费体力为 3。
接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 12，耗费体力为 12。
所以达达总共耗费体力=3+12=15。
可以证明 15 为最小的体力耗费值。

输入格式
输入包括两行，第一行是一个整数 n，表示果子的种类数。
第二行包含 n 个整数，用空格分隔，第 i 个整数 ai 是第 i 种果子的数目。

输出格式
输出包括一行，这一行只包含一个整数，也就是最小的体力耗费值。
输入数据保证这个值小于 2^31。

数据范围
1≤n≤10000,
1≤ai≤20000
输入样例：
3 
1 2 9 
输出样例：
15

题解详见算法基础课笔记（三一），哈夫曼树的原理和应用都有介绍。

本题核心思路就是哈夫曼树的构造方式。

其实这里的最小消耗体力就是结点的带权路径长度（WPL）。

WPL是由每个节点的权值乘上它的路径长度再累加得到；

代码中计算的最小消耗体力是每次合并的两个节点的权值之和的累加。

因为：一个节点的合并次数等于它的深度。

所以：WPL等于最小消耗体力。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;

int main(){
    priority_queue<int,vector<int>,greater<int> > heap;
    
    int n;
    cin >> n;
    
    int a;
    while (n--){
        cin >> a;
        heap.push(a);
    }
    int res = 0;
    while (heap.size() > 1){
        int x = heap.top();heap.pop();
        int y = heap.top();heap.pop();
        int s = x + y;
        heap.push(s);
        res += s;
    }
    
    cout << res << '\n';
    return 0;
}

也可以用大根堆取负来做。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <queue>

using namespace std;

int main()
{
    int n;
    cin >> n;
    priority_queue<int> heap;
    while(n--)
    {
        int x;
        cin >> x;
        heap.push(-x);
    }

    int ans = 0;
    while(heap.size() > 1)
    {
        int a = heap.top();
        heap.pop();
        int b = heap.top();
        heap.pop();

        ans -= a + b;
        heap.push(a + b);
    }

    cout << ans << endl;
}

acwing.149. 荷马史诗（算法进阶指南，有难度）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
追逐影子的人，自己就是影子。 ——荷马
达达最近迷上了文学。
她喜欢在一个慵懒的午后，细细地品上一杯卡布奇诺，静静地阅读她爱不释手的《荷马史诗》。
但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了，达达想通过一种编码方式使得它变得短一些。
一部《荷马史诗》中有 n 种不同的单词，从 1 到 n 进行编号。其中第 i 种单词出现的总次数为 wi。
达达想要用 k 进制串 si 来替换第 i 种单词，使得其满足如下要求:
对于任意的 1≤i,j≤n，i≠j，都有：si 不是 sj 的前缀。
现在达达想要知道，如何选择 si，才能使替换以后得到的新的《荷马史诗》长度最小。
在确保总长度最小的情况下，达达还想知道最长的 si 的最短长度是多少？

一个字符串被称为 k 进制字符串，当且仅当它的每个字符是 0 到 k−1 之间（包括 0 和 k−1）的整数。
字符串 Str1 被称为字符串 Str2 的前缀，当且仅当：存在 1≤t≤m，使得 Str1=Str2[1..t]。
其中，m 是字符串 Str2 的长度，Str2[1..t] 表示 Str2 的前 t 个字符组成的字符串。
注意:请使用 64 位整数进行输入输出、储存和计算。

输入格式
输入文件的第 1 行包含 2 个正整数 n,k，中间用单个空格隔开，表示共有 n 种单词，需要使用 k 进制字符串进行替换。
第 2∼n+1 行：第 i+1 行包含 1 个非负整数 wi，表示第 i 种单词的出现次数。

输出格式
输出文件包括 2 行。
第 1 行输出 1 个整数，为《荷马史诗》经过重新编码以后的最短长度。
第 2 行输出 1 个整数，为保证最短总长度的情况下，最长字符串 si 的最短长度。

数据范围
2≤n≤100000,
2≤k≤9
1≤wi≤10^12
输入样例：
4 2
1
1
2
2
输出样例：
12
2

思路：

由二进制编码扩展到k进制编码。

构造方式：由每次选择最小的2个节点扩展到每次选择最小的k个节点。

如果剩下节点数量不足k个，不足的补0。

证明方法类似。

本题的第一问求编码的最短长度，也就是WPL，和前一题一样。

本题的第二问求树的最长分支的最短长度，换句话说就是在编码最短长度的前提下保证树的分支尽可能短。

这就要求在进行合并操作时，如果有多个权值相同的点时，选择当前深度最小（已合并次数最少）的节点。

所以这里的堆存的是pair，按双关键字排序，第一维是单词出现次数（节点权值），第二维是节点合并次数。

节点个数不够如何补0？

注意到，每次我们都是取k个数，但在最后一次取的时候，可能已经不足k个数可取了，所以不妨在算法的开始，我们就先取掉x个数（补上k-x个 0），使得剩下的n-x个数正好能每次取k个取完。

怎么求 x ？

不妨设补上 x 个节点之后就可以构成一棵 k 叉哈夫曼树。

设 k 度节点个数为 t ，叶子节点（已有节点+补上的节点）个数为 m，已有节点个数为 n 。

建立方程：k*t + 1 = 总节点数; m = n + x; t + m = 总节点数

联立解得：(k-1)*t = n-1+x，等价于x = (n-1) % (k-1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <algorithm>
#include <queue>
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair<LL,int> PLI;

int main(){
    int n,k;
    cin.tie(NULL);
    priority_queue<PLI,vector<PLI>,greater<PLI> > heap;
    
    cin >> n >> k;
    
    LL w;
    while (n--){
        cin >> w;
        heap.push({w,0}); // 加入已有节点，深度为1
    }
    
    while ((heap.size() - 1) % (k - 1)) heap.push({0ll,0}); // 先补上缺少的节点
    
    LL res = 0ll;
    while (heap.size() > 1){
        int depth = 0;
        LL s = 0ll;
        
        for (int i = 0;i < k;i ++){
            auto t = heap.top();
            heap.pop();
            s += t.x,depth = max(depth,t.y);
            // depth维护合并节点的深度，到最后合并到根时，depth也就是最长分支
        }
        heap.push({s,depth+1});// 每次合并子树深度 + 1
        res += s;
    }
    
    cout << res << '\n' << heap.top().y << '\n';
    return 0;
}
坚持原创技术分享，您的支持将鼓励我继续创作！