grant's Blog

记录生活中的点点滴滴

考研算法辅导课笔记（八）

发表于 更新于 分类于 ， ，   阅读次数： Valine：
本文字数： 5.9k 阅读时长 ≈ 5 分钟

真题讲解

2012-41

image-20211206164047298

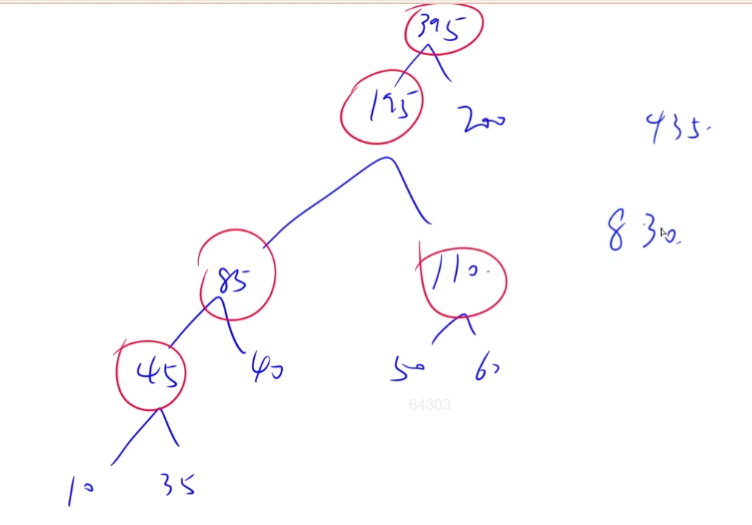
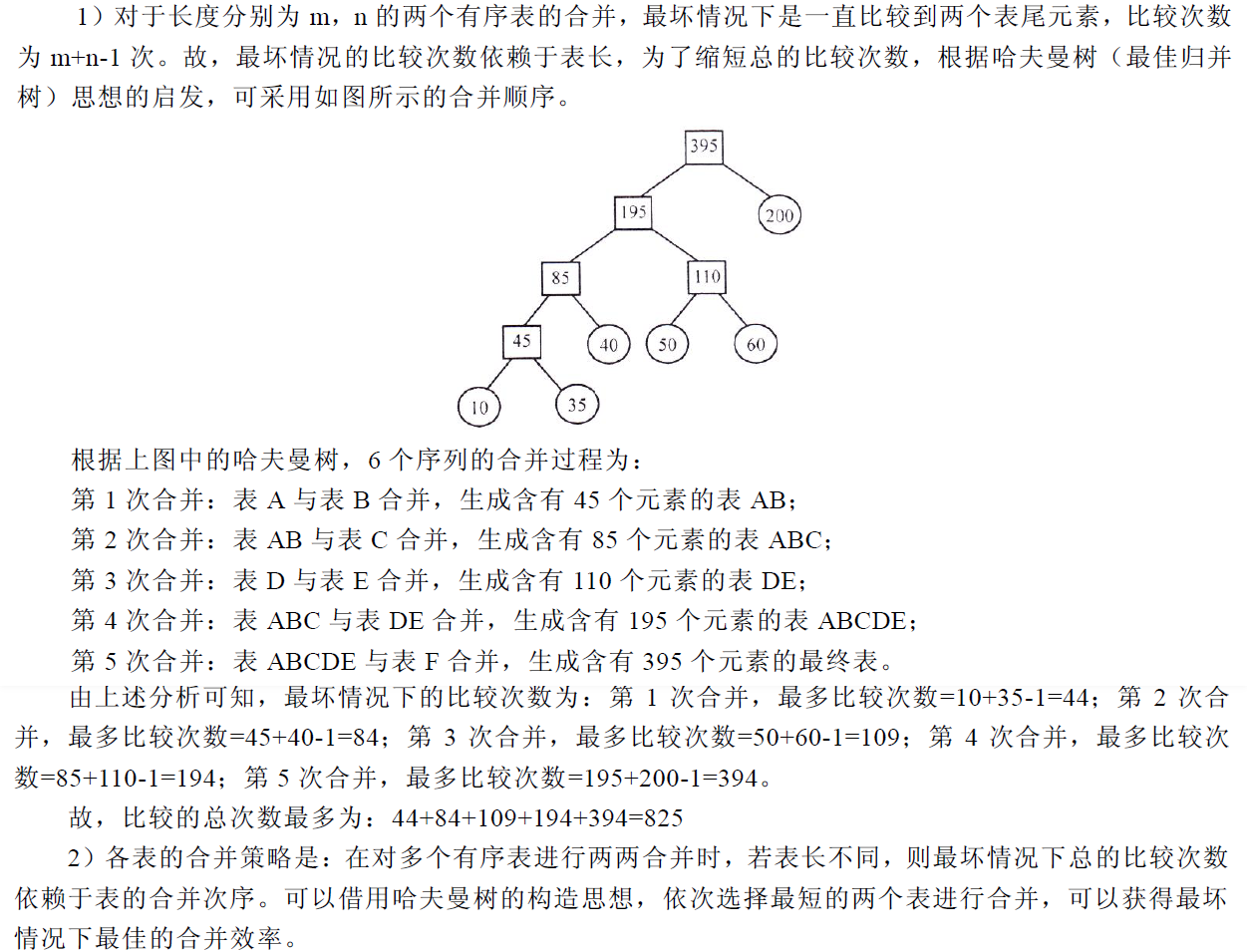
结论：将两个分别含有n，m个元素的有序表合并成一个有序表，其最多的比较次数（最坏情况下）是：n+m-1。

最坏情况下，也就是两个有序表交替合并，例如：1,3,5和2,4，一共有n+m个元素，共需要比较n+m-1次。

合并策略：考察哈夫曼树，就像合并果子一样。

image-20211206164439683

最坏情况下的比较次数，也就是合并代价再减去5次，答案是：825。

参考答案：

image-20211206164747194

2013-4

image-20211206165437765

构造三叉的哈夫曼树，补上(n-1) % (k-1) = 5 % 2 = 1个 0 节点。

计算WPL = 46。

2015-3

image-20211206171439148

解答：

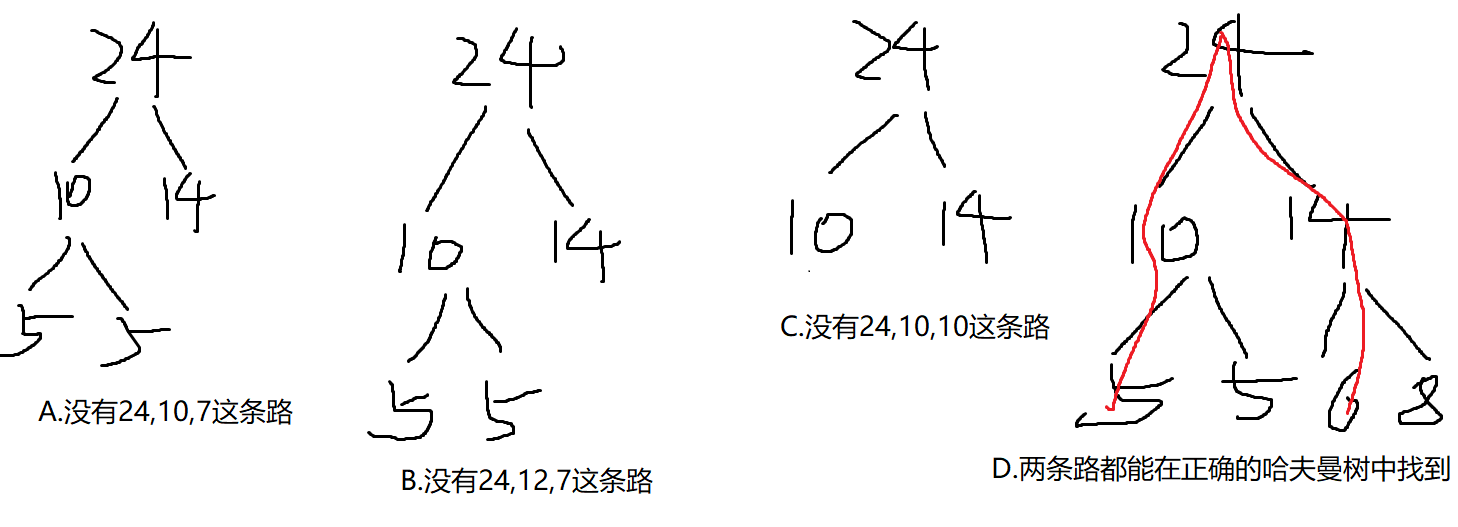
直接根据选项的路径尝试构造哈夫曼树，看看是否合理。

image-20211206172443539

上图中是反着推的，由路径找到一棵合理的哈夫曼树。

正着推的话，并不能确定节点的个数，比如D中权值为10的节点有两个，正着推如果只给1个权值为10的节点是推不出哈夫曼树的。

2020-42

image-20211207143047930

解答：

image-20211207143813635

第七讲 图的基本概念、存储、遍历、拓扑排序

  1. 图的基本概念
    (1) 有向图、无向图
    (2) 度数（出度、入度）
    (3) 简单图：不存在顶点到其自身的边（自环），且同一条边不重复出现（重边）
    (4) 路径、环、简单路径
    (5) 无向完全图：任意两个顶点之间都存在边，有n个顶点的无向完全图有 n × (n - 1) / 2条边
    (6) 有向完全图：任意两个顶点之间都存在方向互为相反的两条弧，有n个顶点的无向完全图有 n × (n - 1) 条弧
    (7) 稀疏图&稠密图：有很少条边或弧的图称为稀疏图，反之称为稠密图，相对的概念。
  2. 图的存储及基本操作
    (1) 邻接矩阵：适用于稠密图，可存有向图、无向图。常用。空间复杂度：O(n^2)。无法存重边。
    (2) 邻接表：适用于稀疏图，可存有向图、无向图。常用。空间复杂度：O(n + m)。可存重边。
    (3) 邻接多重表，适用于稀疏图，可存无向图。不常用。空间复杂度：O(n + m)。可存重边。
    (4) 十字链表，适用于稀疏图，可存有向图、无向图。不常用。空间复杂度：O(n + m)。无法存重边
    (5) 三元组表，适用于稀疏图，可存有向图，无向图。常用于Bellman-Ford算法、Kruskal算法。空间复杂度：O(m)。可存重边。
  3. 图的遍历
    (1) 深度优先搜索。邻接表存储的时间复杂度：O(n + m)。邻接矩阵存储的时间复杂度：O(n^2)
    (2) 广度优先搜索。邻接表存储的时间复杂度：O(n + m)。邻接矩阵存储的时间复杂度：O(n^2)
  4. 拓扑排序

特别注意：408数据结构中的图只考虑简单图（无自环和重边）！！！

以上算法中除了Kruskal算法，大部分都可以将无向图看成是两条有向边的图。

无向图的点的度数不分出度和入度，有向图的点的度数分为出度和入度。

路径、环、简单路径、简单回路：

路径是一个将若干个点连接起来的边的集合。

对于一条路径，如果第一个顶点与最后一个顶点相同，称为回路或环。

自环也算环的一种。

对于一条路径，若顶点不重复出现，则称为简单路径。

对于一条回路，若除第一个顶点与最后一个顶点外的其他顶点不重复出现，则称为简单回路。

特注：不同教材对以上概念的定义不尽相同，以题目和王道为准。

邻接矩阵和邻接表存储图参考王道P206,207。

邻接矩阵存储无向图，看作两条有向边存储，所以这时的矩阵是对称矩阵。

邻接矩阵和邻接表存储稀疏图或者稠密图并没有绝对的限制，只要AC即可。

邻接多重表是邻接表的优化。（怎么存储看王道P209）

当邻接表存储无向图时，每条无向边当作两条有向边来存储；当需要删除一条无向边时，需要两条有向边把它们都删掉，而邻接表查看比较麻烦。

所以引入邻接多重表。（注：这里删边麻烦是王道上的所谓“理论”）

实际上数组模拟邻接表删边很容易，因为我们加边时，两条有向边紧挨着存放（add(a,b),add(b,a)，所以它们编号相邻，很容易找到。

笔试还是以“理论”为主，知道上机不这么写就行。

十字链表是邻接矩阵的优化。

十字链表就是矩阵压缩。（参考博客）

image-20211217205330631

很形象的名字，从左往右拉一条链表（对应正向的路径），再从上往下拉一条链表（对应反向的路径）。

三元组表存边的起点，终点还有边权。（可以看成是对邻接矩阵的空间优化）

图的遍历（dfs和bfs）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 有向非连通图深度优先搜索，邻接表（链表实现）写法
#include <iostream>
using namespace std;
const int N = 105;
bool st[N];

struct Node{
    int val;
    Node* next;

    Node(int _val):val(_val),next(NULL){}
}* head[N];

void add(int x,int y){ // 头插法加入新节点，x-->y
    auto p = new Node(y);
    p->next = head[x];
    head[x] = p;
}

void dfs(int u){

    st[u] = true;
    cout << u << ' ';
    for (auto p = head[u]; p; p = p->next){
        int i = p->val;
        if (!st[i]) dfs(i);
    }
}

int main(){
    int n,m;
    cin >> n >> m;// 点数，边数

    int x,y;
    while (m--){
        cin >> x >> y;
        add(x,y);
    }

    for (int i = 1;i <= n;i ++){
        if (!st[i]) dfs(i);
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
// 有向非连通图广度优先搜索，邻接表（链表实现）写法
#include <iostream>
#include <queue>
using namespace std;
const int N = 105;
bool st[N];

struct Node{
    int val;
    Node* next;

    Node(int _val):val(_val),next(NULL){}
}* head[N];

void add(int x,int y){
    auto p = new Node(y);
    p->next = head[x];
    head[x] = p;
}

void bfs(int u){
    queue<int> q;
    q.push(u);
    st[u] = true;

    while (!q.empty()){
        int u = q.front();
        cout << u << ' ';
        q.pop();

        for (auto p = head[u]; p; p = p->next){
            int t = p->val; // 入队时打上标记
            if (!st[t]) st[t] = true,q.push(t);
        }
    }
}

int main(){
    int n,m;
    cin >> n >> m;

    int x,y;
    while (m--){
        cin >> x >> y;
        add(x,y);
    }

    for (int i= 1;i <= n;i ++){
        if (!st[i]) bfs(i); // 一般写法是把1号节点入队即可，一般不会用BFS处理非连通图
    }
    return 0;
}

acwing.848. 有向图的拓扑序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
给定一个 n 个点 m 条边的有向图，点的编号是 1 到 n，图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。
若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。

输入格式
第一行包含两个整数 n 和 m。
接下来 m 行，每行包含两个整数 x 和 y，表示存在一条从点 x 到点 y 的有向边 (x,y)。

输出格式
共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。
否则输出 −1。

数据范围
1≤n,m≤10^5
输入样例：
3 3
1 2
2 3
1 3
输出样例：
1 2 3

题解参考算法基础课笔记（十七）。

算法大致流程：

  1. 找到所有入度为0的节点入队；
  2. 将入度为0的节点出队，然后将其所指向的所有边删掉；
  3. 重复1,2步骤，直到所有节点都已经入队、出队，则存在拓扑序列，否则不存在。

拓扑序列（有向无环图的序列）不唯一！

不是所有图都存在拓扑序列，比如有环的话就不存在。

有向无环图简称为DAG图。用DAG图表示的工程网络称之为AOV网。

存在拓扑序列等价于无环。

时间复杂度：邻接表O(n+m)，遍历每个顶点和每条边。

算法一：BFS+邻接链表版本。（考研风格写法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5+5;
int d[N],q[N],hh = 0,tt = -1; // d[N]维护入度数量
int n,m;

struct Node{
  int val;
  Node* next;
  
  Node(int _val):val(_val),next(NULL){}
}* head[N];

void add(int a,int b){
    auto p = new Node(b);
    p->next = head[a];
    head[a] = p;
}

bool topsort(){
    for (int i = 1;i <= n;i ++)
        if (!d[i])
            q[++tt] = i;
        
    while (hh <= tt){
        int u = q[hh++];
        
        for (auto p = head[u]; p; p = p->next){
            int t = p->val;
            if (-- d[t] == 0) q[++tt] = t;
        }
    }
    
    if (tt == n-1) return true;
    else return false;
}

int main(){
    cin >> n >> m;
    
    int a,b;
    while (m--){
        cin >> a >> b;
        add(a,b);
        d[b] ++;
    }
    
    if (!topsort()) cout << "-1";
    else{
        for (int i = 0;i < n;i ++)
            cout << q[i] << ' ';
    }
    return 0;
}

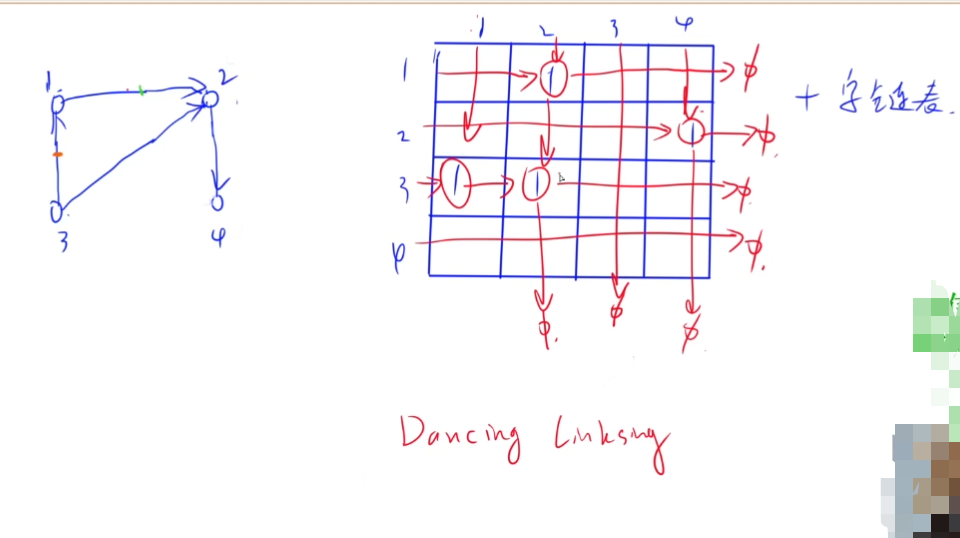
特殊数据：

1
2
3
2 2
1 2
1 2

这样的带重边的图具有拓扑序列：1—>2。

但是带自环（自环属于环）的图没有拓扑序列。

说明：408数据结构中的图只考虑简单图，所以不用考虑自环和重边。

算法二：DFS+邻接链表版本。

  • 如何判断DFS搜索的图无环？

  • 需要对标记数组处理，st[i]共有0，1，2三种值，分别表示：未搜索，正在搜索，已回溯。

这种DFS判环方式在染色法判定二分图以及tarjan算法求解LCA问题中用过！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <vector>
using namespace std;
const int N = 1e5+5;
vector<int> path;
int st[N];
int n,m;

struct Node{
  int val;
  Node* next;
  
  Node(int _val):val(_val),next(NULL){}
}* head[N];

void add(int a,int b){
    auto p = new Node(b);
    p->next = head[a];
    head[a] = p;
}

bool dfs(int u){
    st[u] = 1; // 正在搜索st[u]标记为1
    
    for (auto p = head[u]; p; p = p->next){
        int t = p->val;
        if (!st[t]){
            if (!dfs(t)) return false;
        }
        else if (st[t] == 1) return false; // 如果st[u]标记为1说明重复搜索
        // 这样写也是对的！
        /*if (!st[t] && !dfs(t)) return false;
        else if (st[t] == 1) return false;*/
    }
    
    st[u] = 2; // 表示回溯
    path.push_back(u);
    return true;
}

bool topsort(){
    for (int i = 1;i <= n;i ++){
        if (!st[i] && !dfs(i)) return false;
    }
    return true;
}

int main(){
    cin >> n >> m;
    
    int x,y;
    while (m--){
        cin >> x >> y;
        add(x,y);
    }
    
    if (topsort()){
        for (int i = path.size()-1;i >= 0;i --)
            cout << path[i] << ' ';
        cout << '\n';
    }
    else cout << "-1\n";
    return 0;
}
坚持原创技术分享，您的支持将鼓励我继续创作！