grant's Blog

记录生活中的点点滴滴

考研算法辅导课笔记（五）

发表于 更新于 分类于 ， ，   阅读次数： Valine：
本文字数： 4.8k 阅读时长 ≈ 4 分钟

1.第四讲 树的基本概念、二叉树、树和森林

1.1树的基本概念

408中所有树都是无向有根树。

(1) 树是由根节点和若干棵子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的节点，所定义的关系称为父子关系。父子关系在树的节点之间建立了一个层次结构。在这种层次结构中有一个节点具有特殊的地位，这个节点称为该树的根节点，或称为树根。

(2) 空集合也是树，称为空树。空树中没有节点；

(3) 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；

(4) 节点的度：一个节点含有的子节点的个数称为该节点的度；

(5) 叶节点或终端节点：度为0的节点称为叶节点；

(6) 非终端节点或分支节点：度不为0的节点；

(7) 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；

(8) 兄弟节点：具有相同父节点的节点互称为兄弟节点；

(9) 树的度：一棵树中，最大的节点的度称为树的度；

(10) 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

(11) 树的高度或深度：树中节点的最大层次；

(12) 节点的祖先：从根到该节点所经分支上的所有节点；

(13) 子孙：以某节点为根的子树中任一节点都称为该节点的子孙；

(14) 森林：由棵互不相交的树的集合称为森林。

树中节点的度和图中节点的度不太一样，树中节点的度是含有子节点的个数，图中节点的度是和该点连接的点的个数。

一棵包含n个点的树的边数是n-1。

1.2二叉树

(1) 二叉树的定义及其主要特征

a. 二叉树的基本形态：空二叉树、单节点二叉树、左子树、右子树

b. 性质：

  • [1] 在非空二叉树中，第i层上至多有2^(i-1) 个结点。（i >= 1）
  • [2] 深度为k的二叉树至多有2^k - 1个结点（1 推 2）
  • [3] 对任何一棵二叉树，若其叶子结点数为n0，度为2的结点数为n2，则n0 = n2 + 1。
  • [4] n个结点的完全二叉树深度为：log2(n)向下取整 + 1，$\lfloor log_2(n) \rfloor + 1$
  • [5] 二叉树的堆式存储: 节点编号x的父亲：$\lfloor x/2 \rfloor$，左儿子：2x，右儿子：2x+1（节点编号从1开始，从上至下，从左至右）

c. 两种特殊的二叉树

  • [1] 满二叉树：一颗深度为k且有2^k-1个结点的二叉树
  • [2] 如果深度为k,有n个结点的二叉树，当且仅当其每个结点都与深度为k的满二叉树中编号从1到n的结点一一对应，该二叉树称为完全二叉树，完全二叉树的度为1的节点个数为0或1.

(2) 二叉树的顺序存储结构和链式存储结构

(3) 二叉树的遍历

a. 前序遍历

b. 中序遍历

c. 后序遍历

d. 根据前序 + 中序重建二叉树（AcWing 18)

证明性质[3]：

设树的点数为n。

点数方程：$n = n_0 + n_1 + n_2$，边数方程：$n-1 = 0n_0 + 1n_1 + 2*n_2$。

联立后得证。

深度为k（从1开始算）的完全二叉树的有n个节点，则：$2^{k-1} <= n <= 2^k - 1.$

易证：当前k-1层节点满了，第k层只有一个节点时取下界；当前k-1层节点满了，第k层节点也满了取上界。

由这个性质也能推出上面的[4]。

二叉树的存储结构：

分为顺序存储和链式存储。（见王道P124，P125）

顺序存储和堆的存储方式一样，节点编号从1开始，从上至下，从左至右。

顺序存储到哪里结束？与一棵完全二叉树对应。（真题考察过）

链式存储用二叉链表实现。

二叉树的遍历：

有先序、中序和后序三种遍历方式，分别是根左右，左根右，左右根。

还有一种层次遍历方式。

由遍历序列构造一棵二叉树：

前序+中序 或者 后序+中序可以唯一确定。

image-20211122215402530

前序可以确定根的编号，中序可以确定左右子树的大小，然后就确定了左右子树的前序和中序序列。

前序+后序无法唯一确定一棵二叉树：

若前序有根和左右子树，可以唯一确定；

若前序只有根和一棵子树，则无法唯一确定。（因为无法知道仅有的这棵子树是左子树还是右子树）

image-20211129221840737

18. 重建二叉树

输入一棵二叉树前序遍历和中序遍历的结果，请重建该二叉树。

注意:

  • 二叉树中每个节点的值都互不相同；
  • 输入的前序遍历和中序遍历一定合法；

样例

1
2
3
4
5
6
7
8
9
10
11
给定：
前序遍历是：[3, 9, 20, 15, 7]
中序遍历是：[9, 3, 15, 20, 7]

返回：[3, 9, 20, null, null, 15, 7, null, null, null, null]
返回的二叉树如下所示：
    3
   / \
  9  20
    /  \
   15   7

思路：

参考题解： y总官方题解。

前序遍历确定根是谁，中序遍历确定根的位置。

然后递归创建出二叉树。

时间复杂度分析：

初始时用哈希表存储每个节点的值到中序遍历下标（0到n-1）的映射，这样我们在递归到每个节点时，在中序遍历中查找根节点位置的操作，只需要 O(1) 的时间。此时，创建每个节点需要的时间是 O(1)，所以总时间复杂度是 O(n)。

图解：

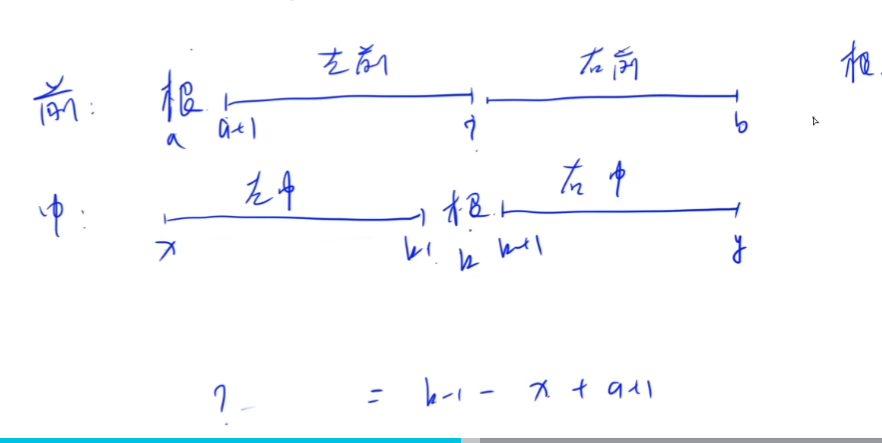
image-20211123225503455

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    unordered_map<int,int> pos;
    vector<int> preorder,inorder; // 可以创建两个vector，也可以将_preorder传引用到build
    
    TreeNode* build(int a,int b,int x,int y){ // 分别对应前序、中序的左右边界下标
        // 当左右边界下标相等时表示序列含有1个元素
        if (a > b) return NULL; // 当左 < 右时表示子树为空
        auto root = new TreeNode(preorder[a]);
        int k = pos[preorder[a]]; // 前序的第一个就是根，查找根在中序的下标
        // 递归创建二叉树
        root->left = build(a + 1, k - 1 - x + a + 1, x, k - 1);
        root->right = build(k - 1 - x + a + 2, b, k + 1, y);
        return root;
    }
    
    TreeNode* buildTree(vector<int>& _preorder, vector<int>& _inorder) {
        preorder = _preorder,inorder = _inorder;
        
        int n = preorder.size();
        
        for (int i = 0;i < n;i ++){
            pos[inorder[i]] = i;
        }
        
        return build(0, n - 1, 0, n - 1);
    }
};

// 不用哈希表的版本： 笔试写法
// 将19行替换为下面的代码，31~33行删掉，时间复杂度为：O(n^2)
int k = -1; // 前序的第一个就是根，查找根在中序的下标
for (int i = x;i <= y;i ++){
    if (inorder[i] == root->val)
        k = i;
}

1.3线索二叉树

(4) 线索二叉树的基本概念和构造

对二叉树节点的指针域做如下规定：

a. 若节点有左孩子，则Lchild指向左孩子，否则指向直接前驱；右孩子同理；

b. 增加两个标志域，Ltag表示指向的是子节点还是前驱；Rtag同理

c. 指向前驱和后继的指针叫做线索。按照某种次序遍历，加上线索的二叉树称之为线索二叉树

引入线索二叉树是为了加快找到节点的前驱和后继的速度。

线索二叉树通过线索链表实现，其中指向前驱和后继的指针称为线索。

根据遍历序列，可以将线索二叉树分为中序、先序、后序线索二叉树。

具体定义规则如果不理解请参考王道教材P136.

1.4树、森林

(1) 树的存储结构
a. 只存父节点
b. 邻接表存储所有子节点
c. 左儿子右兄弟

(2) 森林F与二叉树T的转换
a. 原树中叶子节点数 = 转换后的树中有右儿子的节点数 + 1
b. F的前序遍历就是T的前序遍历
c. F的后序遍历就是T的中序遍历

(3) 树和森林的遍历
a. 前序遍历
b. 后序遍历

树常用的三种存储方式：双亲表示法，孩子表示法，孩子兄弟表示法。

1.双亲表示法。

双亲表示法是顺序存储方式。

存储方式和并查集很像。

树中每个节点用结构体数组顺序存储，结构体包括：数据域，父节点的下标。

关于树和二叉树的顺序存储方式的区别：

  • 二叉树属于树，所以二叉树可以用树的顺序存储；

  • 由于不确定分叉大小，树不能用二叉树的顺序存储。

2.孩子表示法。

其实就是树的邻接表存储，当作图来存。

3.孩子兄弟表示法。（笔试常考）

又称二叉树表示法。（左孩子右兄弟）

本质上就是一个邻接表。

这种存储方式最大的优点就是方便实现树（森林）转换为二叉树的操作。

每个节点包含三部分内容：

  1. 节点值；
  2. 指向第一个孩子的指针；
  3. 指向下一个兄弟的指针。

具体定义规则如果不理解请参考王道教材P161,162.

image-20211128205126385

树的遍历：

只有三种方式：前序和后序遍历，还有层次遍历。

树没有中序遍历。

森林F与二叉树T的转换：

森林与二叉树转换的性质：原树中叶子节点数 = 转换后的树中有右儿子的节点数 + 1

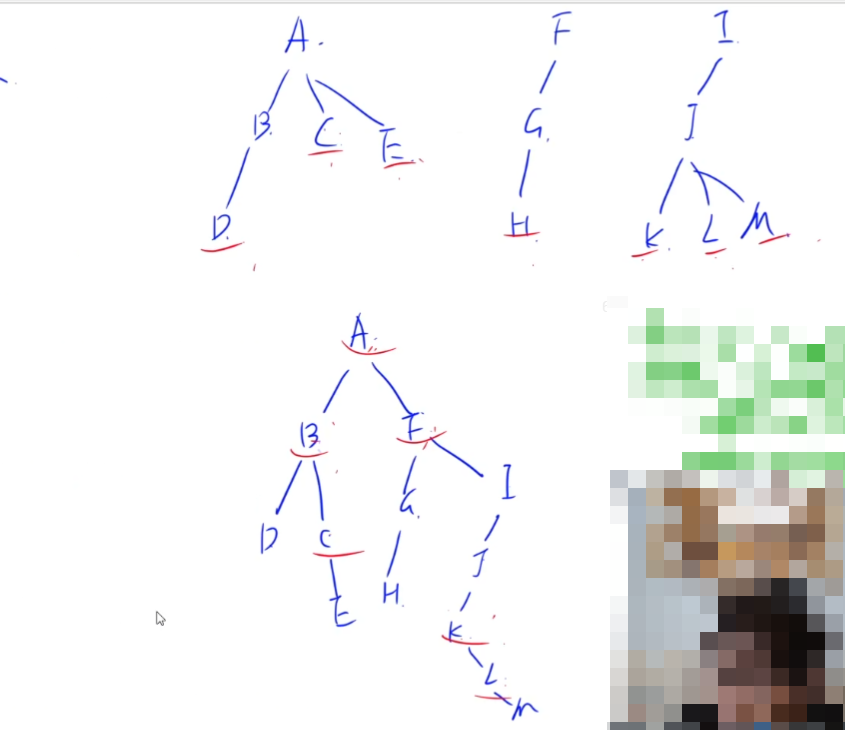
image-20211128205346009

两条转化规则：

  • F的前序遍历就是T的前序遍历
  • F的后序遍历就是T的中序遍历

F的后序遍历也可以称为中序遍历，原因看王道教材P164.

拿上图的森林与二叉树举例：

森林的前序遍历和二叉树的前序遍历都是：ABDCEFGHIJKLM。

森林的后序遍历和二叉树的中序序遍历是一样的。

树的遍历方式是递归定义的，下图可以验证这条性质。

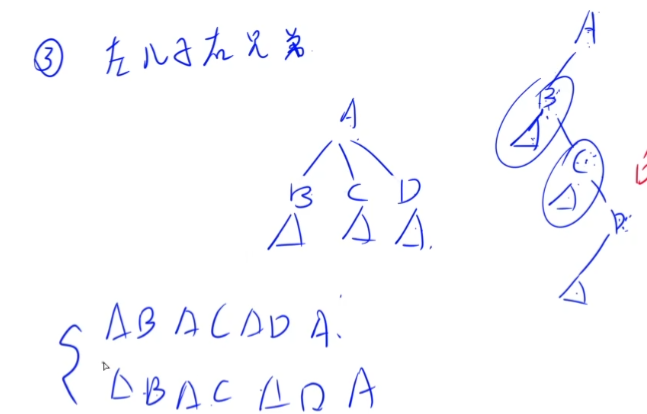
image-20211129220509836

2011-6

image-20211129223429881

解：

选择题，采用“特殊值“法，构造一棵特殊的树。

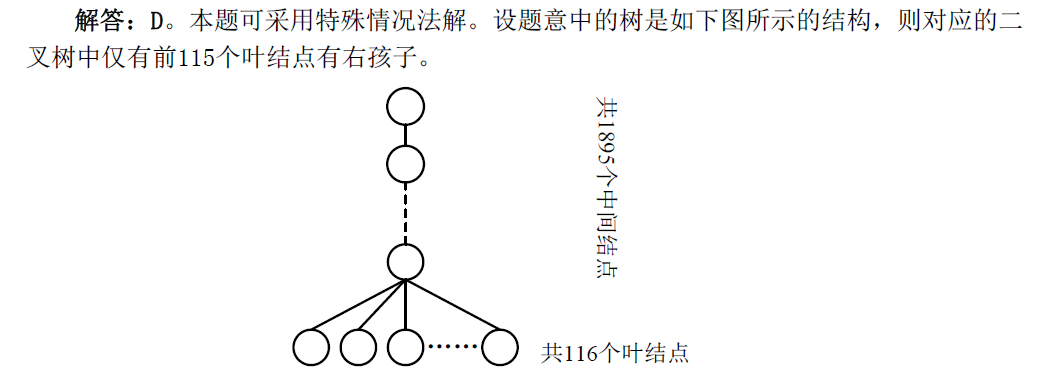
image-20211129223704494

2014-5

image-20211129224920283

森林中叶节点，也就是没有孩子的节点，对应二叉树的是没有左孩子的节点（因为左孩子右兄弟）。

2014-41

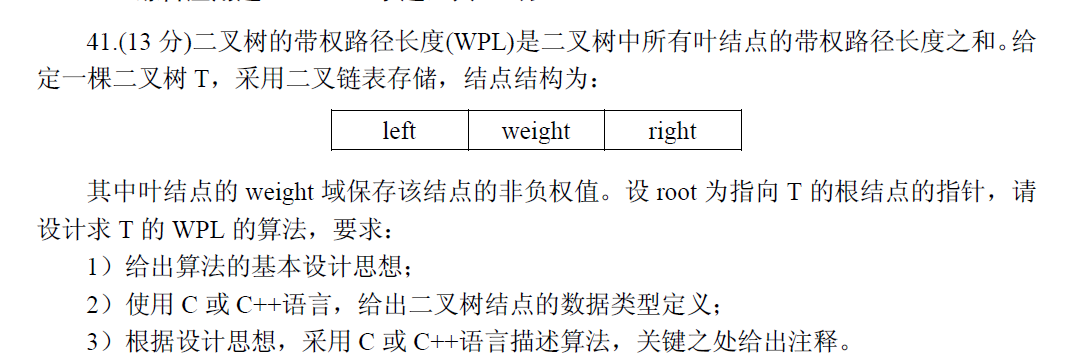
image-20211130143311751

accwing.3766. 二叉树的带权路径长度

二叉树的带权路径长度(WPL)是二叉树中所有叶结点的带权路径长度之和，也就是每个叶结点的深度与权值之积的总和。

给定一棵二叉树 T，请你计算并输出它的 WPL。

注意，根节点的深度为 0。

样例

1
2
3
4
5
6
7
8
输入：二叉树[8, 12, 2, null, null, 6, 4, null, null, null, null]如下图所示：
    8
   / \
  12  2
     / \
    6   4

输出：32

数据范围

二叉树结点数量不超过 1000。

每个结点的权值均为不超过 100 的非负整数。

带权路径的解释：每个节点的带权路径长度 = 叶节点权值 * 叶节点到根的路径长度。

做法：简单的dfs遍历树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int dfs(TreeNode* root,int depth){
        if (!root) return 0;
        if (!root->left && !root->right) return root->val * depth;
        return dfs(root->left,depth + 1) + dfs(root->right,depth + 1);
    }

    int pathSum(TreeNode* root) {
        return dfs(root,0);
    }
};
坚持原创技术分享，您的支持将鼓励我继续创作！