2.2栈和队列的应用 2.2.1栈的应用 表达式求值(中缀表达式转后缀表达式、括号匹配)、DFS。
DFS也就是递归,有一类特殊的递归:尾递归。
尾递归:
若函数在尾位置调用自身(或是一个尾调用本身的其他函数等等),则称这种情况为尾递归 。尾递归也是递归的一种特殊情形。
考点:尾递归 可以等价于迭代写法,不需要用栈来实现 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <iostream> using namespace std ;void f (int n) if (n <= 0 ) return ; printf ("%d\n" ,n); f(n-1 ); } int main () f(7 ); cout << "-----------\n" ; for (int i = 7 ; i; -- i) cout << i << '\n' ; return 0 ; }
出栈顺序:
参考文章1: https://oi-wiki.org/math/combinatorics/catalan/。
参考文章2: https://zhuanlan.zhihu.com/p/391237550。
一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?
这是一个Catalan 数列问题,卡特兰数 。
答案是: $\frac {\binom{2n}{n}} {n+1}$.
表达式求值:
3302. 表达式求值 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 给定一个表达式,其中运算符仅包含 +,-,*,/(加 减 乘 整除),可能包含括号,请你求出表达式的最终值。 注意: 数据保证给定的表达式合法。 题目保证符号 - 只作为减号出现,不会作为负号出现,例如,-1+2,(2+2)*(-(1+1)+2) 之类表达式均不会出现。 题目保证表达式中所有数字均为正整数。 题目保证表达式在中间计算过程以及结果中,均不超过 2^31−1。 题目中的整除是指向 0 取整,也就是说对于大于 0 的结果向下取整,例如 5/3=1,对于小于 0 的结果向上取整,例如 5/(1−4)=−1。 C++和Java中的整除默认是向零取整;Python中的整除"//"默认向下取整,因此Python的eval()函数中的整除也是向下取整,在本题中不能直接使用。 输入格式 共一行,为给定表达式。 输出格式 共一行,为表达式的结果。 数据范围 表达式的长度不超过 10^5。 输入样例: (2+2)*(1+1) 输出样例: 8
题解详见算法基础课笔记(十四)。
考研中代码不一定要完全会写(推荐最好熟练掌握),但是表达式求值的流程一定要牢牢掌握。
使用两个栈来求表达式的值,一个操作数栈,一个操作符栈。
先背上面思路,再背下面代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 #include <iostream> #include <stack> #include <cstring> #include <algorithm> #include <unordered_map> using namespace std ;stack <int > num;stack <char > op;void eval () auto b = num.top();num.pop(); auto a = num.top();num.pop(); auto c = op.top();op.pop(); int x; if (c == '+' ) x = a + b; if (c == '-' ) x = a - b; if (c == '*' ) x = a * b; if (c == '/' ) x = a / b; num.push(x); } int main () unordered_map <char ,int > pr{{'+' ,1 },{'-' ,1 },{'*' ,2 },{'/' ,2 }}; string str; cin >> str; for (int i = 0 ;i < str.size();i ++){ char c = str[i]; if (isdigit (c)){ int x = 0 ,j = i; while (j < str.size() && isdigit (str[j])) x = x*10 + str[j++] - '0' ; i = j-1 ; num.push(x); } else if (c == '(' ) op.push(c); else if (c == ')' ){ while (op.top() != '(' ) eval(); op.pop(); } else { while (op.size() && op.top() != '(' && pr[op.top()] >= pr[c]) eval(); op.push(c); } } while (op.size()) eval(); cout << num.top() << '\n' ; return 0 ; }
中缀表达式转后缀表达式:
只需要将上面的程序修改一下就行了。
不需要数栈,遇到数直接输出就行,进行运算时直接输出运算符。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <iostream> #include <stack> #include <cstring> #include <algorithm> #include <unordered_map> using namespace std ;stack <char > op;void eval () auto c = op.top();op.pop(); cout << c << ' ' ; } int main () unordered_map <char ,int > pr{{'+' ,1 },{'-' ,1 },{'*' ,2 },{'/' ,2 }}; string str; cin >> str; for (int i = 0 ;i < str.size();i ++){ char c = str[i]; if (isdigit (c)){ int x = 0 ,j = i; while (j < str.size() && isdigit (str[j])) x = x*10 + str[j++] - '0' ; i = j-1 ; cout << x << ' ' ; } else if (c == '(' ) op.push(c); else if (c == ')' ){ while (op.top() != '(' ) eval(); op.pop(); } else { while (op.size() && op.top() != '(' && pr[op.top()] >= pr[c]) eval(); op.push(c); } } while (op.size()) eval(); return 0 ; }
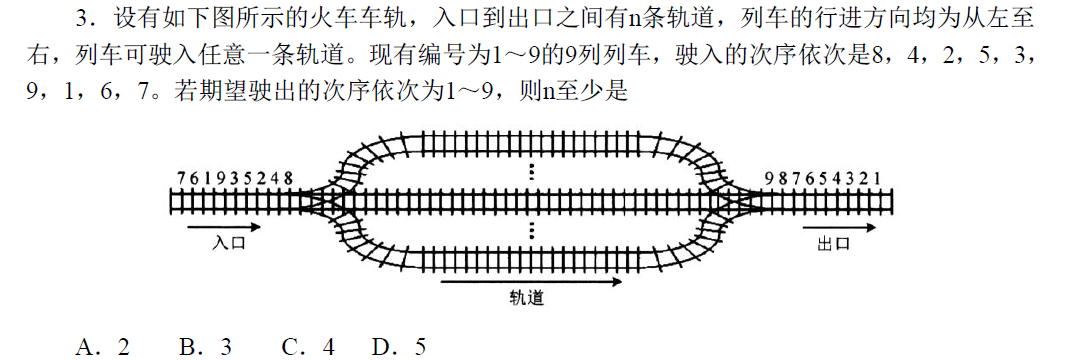
2016-3
本题的思想有点像导弹拦截问题。
每条轨道就相当于一个队列。
注意不是一条轨道只能走一辆火车。
思路:
每进来一个编号,先在现有轨道中找到离它最近且比它小的数字,如果所有数都比它大,就新开一条轨道。
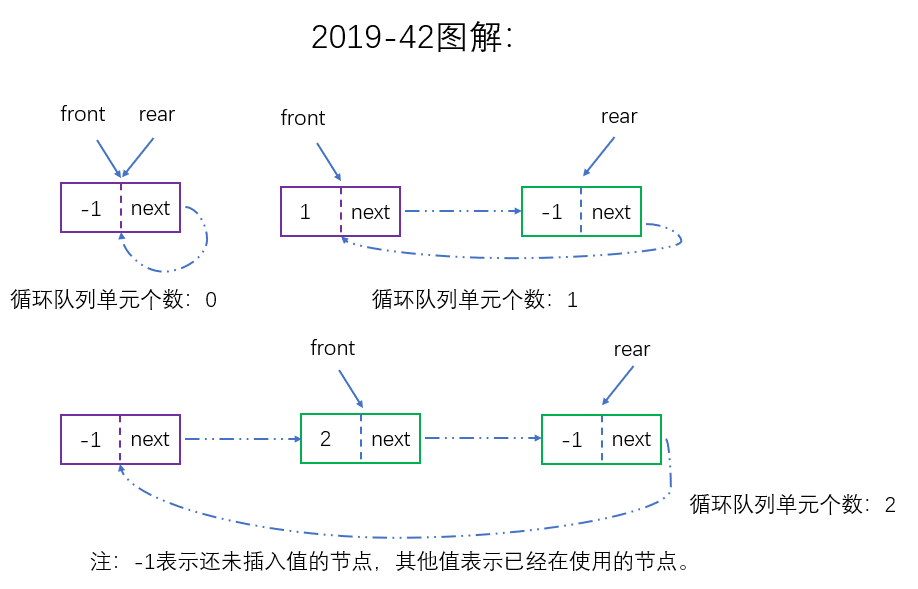
2019-42
本题并没有要求写代码,只要回答问题就行。
(1)入队要求增加队列占用空间,如果用数组实现只能将数据移入一个更大的数组,不能保证入队操作时间复杂度为:O(1);所以应该选择链式存储结构。
(2)如图所示。(队头,队尾指针的指向并不唯一,有多种答案)
(3)如图所示。
(4) 注意:入队出队时记得判断队满和队空情况。
答案的链队列格式类似考研算法笔记(三)中的示例链队列,只不过这里从一般队列改成了循环队列。