1.5:前缀和
前缀和知识在蓝桥杯系列(七)、(八)中有详细讲解。
这里简单回顾一下。
一维前缀和 —— 模板题 AcWing 795. 前缀和
1 | S[i] = a[1] + a[2] + ... a[i] |
预处理时间复杂度:O(n),每次查询时间复杂度:O(1)。
1 |
|
二维前缀和 —— 模板题 AcWing 796. 子矩阵的和
1 | S[i, j] = 第i行j列格子左上部分所有元素的和 |
预处理时间复杂度:O(n*m),每次查询时间复杂度:O(1)。
1 |
|
1.6:差分
差分知识在蓝桥杯系列(二九)中有详细讲解。
这里简单回顾一下。
差分是前缀和的逆运算。
一维差分 —— 模板题 AcWing 797. 差分
1 | 给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c |
1 |
|
其实上面代码只需要一个b[N]数组就可以,差分数组初始化只要读入int x就行,不需要另外的数组。
二维差分 —— 模板题 AcWing 798. 差分矩阵
1 | 给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c: |
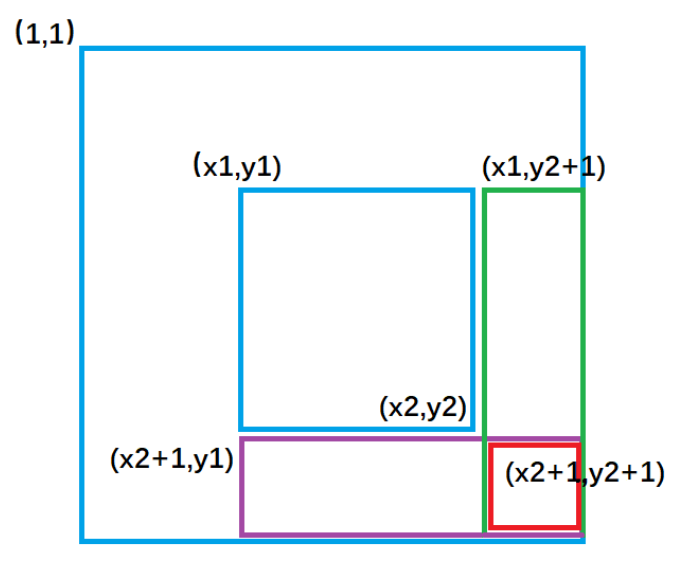
1 |
|
同一维差分一样,只要一个b数组就行,不需要再另外开一个数组。
1.7:练习
1.7.1快排.acwing.786.第k个数
1 | 给定一个长度为 n 的整数数列,以及一个整数 k,请用快速选择算法求出数列从小到大排序后的第 k 个数。 |
考察算法:快速选择排序。(选择数列中第k小数)

时间复杂度分析:每次递归一层会减少到一半。
T = n + n/2 + n/4 + ... = n*(1 + 1/2 + 1/4 + ...) <= 2*n,所以为:O(n)。
1 |
|

