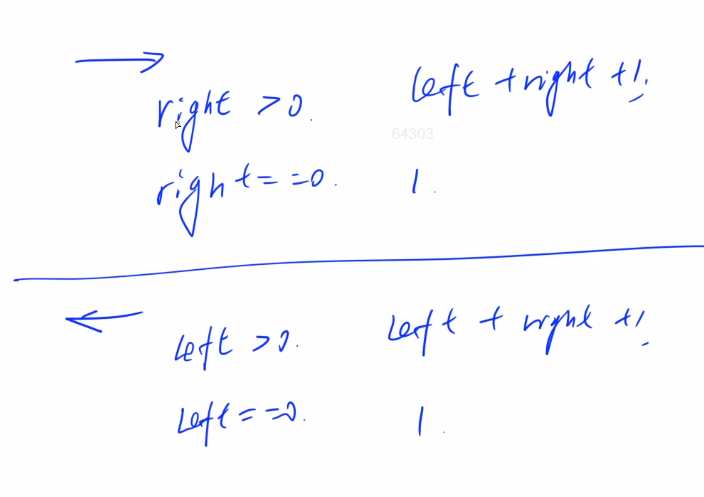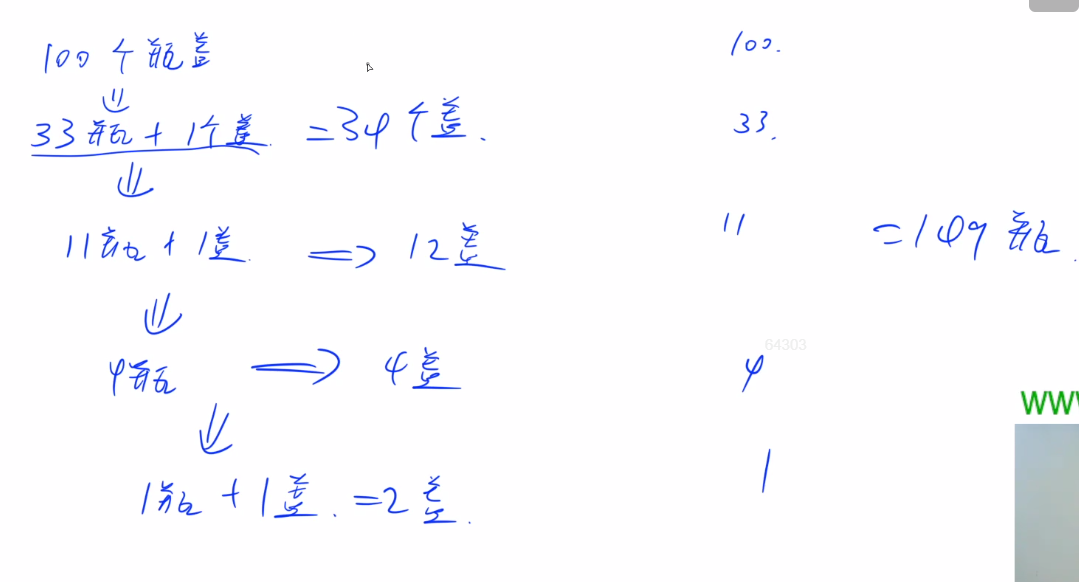1.2 acwing.1211. 蚂蚁感冒(第五届AB组)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| 长 100 厘米的细长直杆子上有 n 只蚂蚁。
它们的头有的朝左,有的朝右。
每只蚂蚁都只能沿着杆子向前爬,速度是 1 厘米/秒。
当两只蚂蚁碰面时,它们会同时掉头往相反的方向爬行。
这些蚂蚁中,有 1 只蚂蚁感冒了。
并且在和其它蚂蚁碰面时,会把感冒传染给碰到的蚂蚁。
请你计算,当所有蚂蚁都爬离杆子时,有多少只蚂蚁患上了感冒。
输入格式
第一行输入一个整数 n, 表示蚂蚁的总数。
接着的一行是 n 个用空格分开的整数 Xi, Xi 的绝对值表示蚂蚁离开杆子左边端点的距离。
正值表示头朝右,负值表示头朝左,数据中不会出现 0 值,也不会出现两只蚂蚁占用同一位置。
其中,第一个数据代表的蚂蚁感冒了。
输出格式
输出1个整数,表示最后感冒蚂蚁的数目。
数据范围
1<n<50,
0<|Xi|<100
输入样例1:
3
5 -2 8
输出样例1:
1
输入样例2:
5
-10 8 -20 12 25
输出样例2:
3
|
思路:
本题不属于任何算法。
首先要看出来,这里两只蚂蚁碰面掉头,其实等价于穿过去。掉头只是幌子,不要想复杂了。
因为相撞之后两只蚂蚁都感冒了,掉不掉头其实无所谓,毕竟都感冒了,这样的话这题就简单多了。
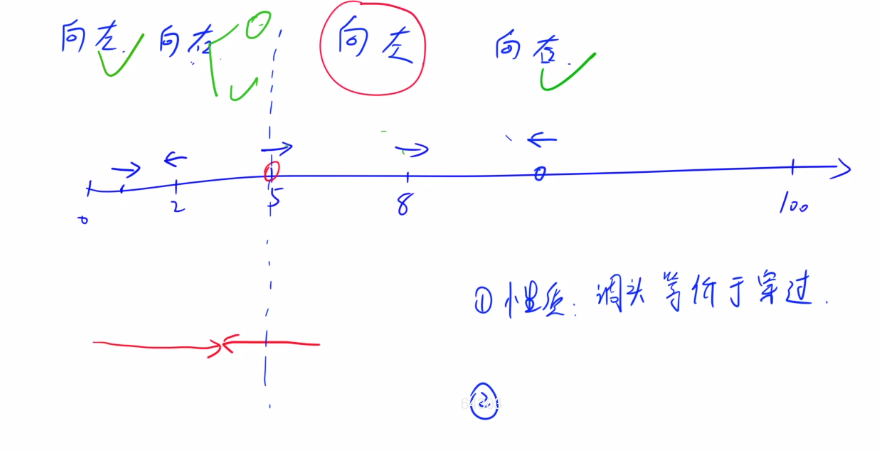
以第一只感冒蚂蚁(向右走)为分界,考虑左右两边的蚂蚁。

第一只感冒蚂蚁(向左走)情况类似。
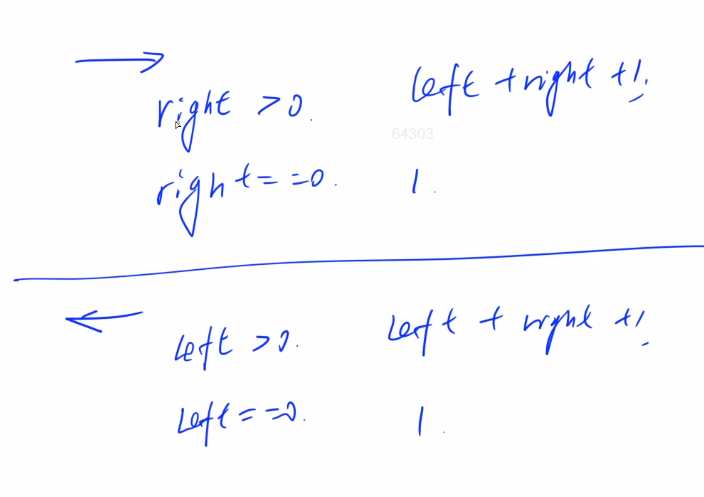
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 55;
int n;
int x[N];
int main(){
cin >> n;
for (int i = 0;i < n;i++) cin >> x[i];
int left = 0,right = 0;
for (int i = 1;i < n;i++)
if (abs(x[i]) < abs(x[0]) && x[i] > 0) left++;
else if (abs(x[i]) > abs(x[0]) && x[i] < 0) right++;
if (x[0] > 0 && right == 0 || x[0] < 0 && left == 0) cout << 1;
else cout << left + right + 1;
return 0;
}
|
1.3 acwing.1216. 饮料换购(第六届C++A/C组)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| 乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊C型饮料,凭3个瓶盖可以再换一瓶C型饮料,并且可以一直循环下去(但不允许暂借或赊账)。
请你计算一下,如果小明不浪费瓶盖,尽量地参加活动,那么,对于他初始买入的 n 瓶饮料,最后他一共能喝到多少瓶饮料。
输入格式
输入一个整数 n,表示初始买入的饮料数量。
输出格式
输出一个整数,表示一共能够喝到的饮料数量。
数据范围
0<n<10000
输入样例:
100
输出样例:
149
|
思路:
先手动模拟一下。
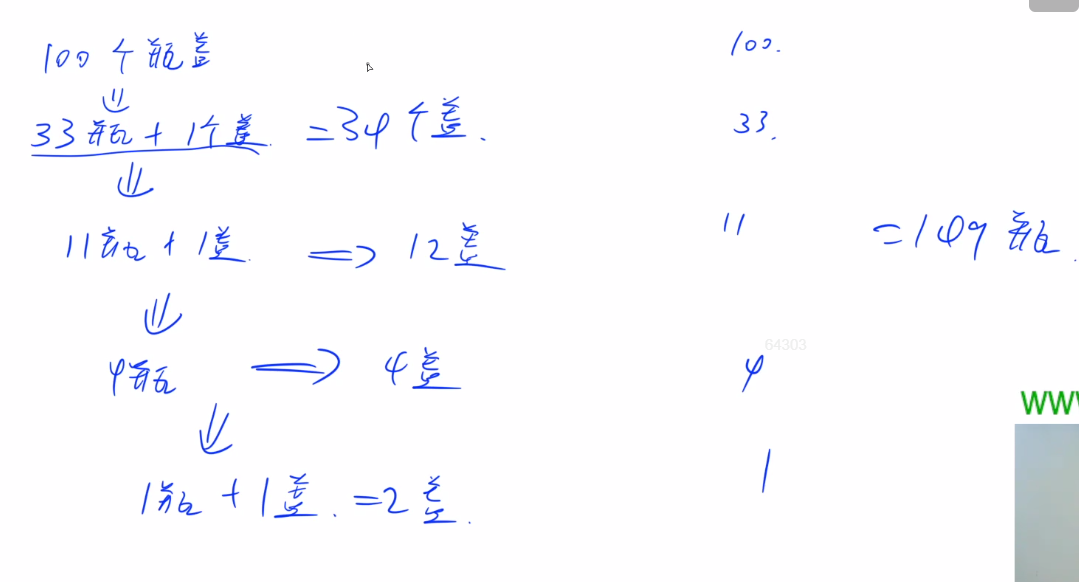

粗略计算一下,取n=10000时,每次除以3,大概需要迭代8,9次,时间完全没问题。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
#include <iostream>
using namespace std;
int main(){
int n;
cin >> n;
int res = n;
while (n >= 3){
res += n / 3;
n = n / 3 + n % 3;
}
cout << res;
return 0;
}
|
补充小知识:如何求上取整?
有一个公式,将上取整转化为下取整,因为C++计算int除法时默认下取整,$\lceil \frac a b \rceil = \lfloor \frac {a+b-1} b \rfloor$
证明如下:(PS:严格证明请参考这里)
分情况讨论:
- 当
a mod b = 1,2,...,b-1时,(a mod b)+b-1 = b,b+1,...,b+b-2,这多余部分除以b下取整都是1,而左右两边的整数部分又相同,所以成立;(即a%b != 0时,上取整等于下取整+1)
- 当
a mod b = 0时,(a mod b)+b-1 = b-1,而$\frac {b-1}b$下取整是0,而左右两边的整数部分又相同,所以成立。(即a%b = 0时,上取整等于下取整)
向下取整的运算称为Floor,用数学符号⌊⌋表示;向上取整的运算称为Ceiling,用数学符号⌈⌉表示。
例如:
⌊59/60⌋=0 ⌈59/60⌉=1 ⌊-59/60⌋=-1 ⌈-59/60⌉=0