grant's Blog

记录生活中的点点滴滴

蓝桥杯学习总结（九）

发表于 更新于 分类于 ，   阅读次数： Valine：
本文字数： 3.2k 阅读时长 ≈ 3 分钟

100里程碑！！！

image-20210428224908874

2.4 acwing.1230. K倍区间（蓝桥杯第八届B组）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
给定一个长度为 N 的数列，A1,A2,…AN，如果其中一段连续的子序列 Ai,Ai+1,…Aj 之和是 K 的倍数，我们就称这个区间 [i,j] 是 K 倍区间。
你能求出数列中总共有多少个 K 倍区间吗？

输入格式
第一行包含两个整数 N 和 K。
以下 N 行每行包含一个整数 Ai。

输出格式
输出一个整数，代表 K 倍区间的数目。

数据范围
1≤N,K≤100000,
1≤Ai≤100000
输入样例：
5 2
1
2
3
4
5
输出样例：
6

思路：

在比赛时，未必能一下就想到最优的解法，可以先从简单的暴力做法写起，拿到一部分分数，不要放弃。

image-20210428230845430

对于第三重循环计算一段区间的总和，可以用前缀和简化。

有了如下想法：

1
2
3
4
5
for(int i = 1; i <= n; i ++) s[i] = s[i - 1] + a[i]; // 求前缀和

for(int r = 1; r <= n; r ++)
    for(int l = 1; l <= r; l ++)
        if((s[r] - s[l - 1]) % k == 0) ans ++;

但这样时间复杂度是：O(n^2)，还不够优秀。

我们枚举了左端点和右端点，可以进一步优化：只枚举右端点。

上面的循环写法等价于：求s[r]%k == s[0~r-1]%k。

这个式子的意思就是：在模k的意义下，求之前所有点和当前点有多少个相等。（有点DP的味道！）

我们发现可以存余数来判断是否满足要求，则可以优化成O(n)。

先开一个数组cnt[i]来存余数是i的数有多少个，用空间换时间。

附上一份高赞题解：https://www.acwing.com/solution/content/6909/

我们可以用一个数组cnt，规定cnt[i]表示当前位置之前，前缀和取模后等于i的个数，以后每出现一次前缀和（取模后）和它相等，那么k倍区间就加上cnt[s[i] % k]，然后cnt[s[i] % k]++。

res += cnt[s[i] % k];先执行，因为要判断当前区间右端点的左边的同余元素，再更新当前位置。

cnt=0必须加上，当右端点为1时，若刚好是k的倍数，此时答案应该+1，若没有这句不会+1。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// y总题解
#include <cstdio>
using namespace std;
typedef long long LL; // 可能爆int
const int N = 100010;

LL s[N],cnt[N];
int n,k;
int main(){
    scanf("%d%d",&n,&k);
    for (int i = 1;i <= n;i++){
        scanf("%lld",&s[i]);
        s[i] += s[i-1]; // 也可以在预处理前缀和时直接对k取模
    }
    LL res = 0;
    cnt[0] = 1;
    for (int i = 1;i <= n;i++){ // 枚举右端点
        res += cnt[s[i]%k];
        cnt[s[i]%k]++;
    }
    printf("%lld",res);
    return 0;
}

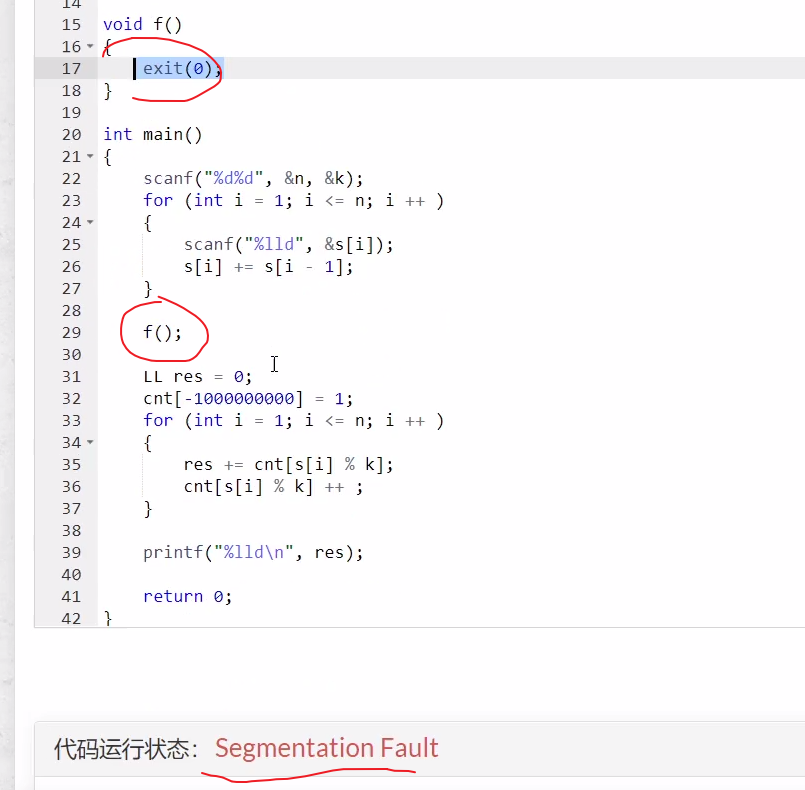
补充：有关段错误的调试方法，使用exit(0)进行二分判断出错位置。

对于类似的没有输出信息的错误都可以采用这种二分找错的方法。

image-20210429081035194

三 数学与简单DP

1.数学问题

关于数学问题，OIwiki是个好东西！

1.1 acwing.1205. 买不到的数目（第四届A组）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
小明开了一家糖果店。
他别出心裁：把水果糖包成4颗一包和7颗一包的两种。
糖果不能拆包卖。
小朋友来买糖的时候，他就用这两种包装来组合。
当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。
你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。

大于17的任何数字都可以用4和7组合出来。
本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。

输入格式
两个正整数 n,m，表示每种包装中糖的颗数。

输出格式
一个正整数，表示最大不能买到的糖数。

数据范围
2≤n,m≤1000，
保证数据一定有解。

输入样例：
4 7
输出样例：
17

思路：

这是一个非常经典的问题，可以当作一个定理来用。（靠数学积累了）

先分析一下：

根据学过的代数知识，对于给定的数n，m，显然有：$(n,m)|n,(n,m)|m$，推出：$(n,m)|xn+ym$

也就是说，n和m的线性组合一定是(n,m)的倍数，只有这种情况才有解。

给定a，b，若d=gcd(a,b)>1,则一定不能凑出最大数。答案要求a，b互质！

为什么呢？

如果d=gcd(a,b)>1，那么一定可以找到一个极大的数t，满足$(a,b)\nmid t$，这个数可以无限大，所以无解；

而如果d=gcd(a,b)=1，那么所有极大的数t一定满足$1\mid t$，这是显然的，所以有解。

没思路？试试打表找规律！（对于数学问题，没思路不妨试试打表）

补充知识：裴蜀定理，https://oi-wiki.org/math/bezouts/

是一个关于最大公约数的定理。

其内容是：

设a, b是不全为零的整数, 则存在整数x, y,使 $a x+b y=\operatorname{gcd}(a, b).$

证明过程看上面链接。它的一个重要推论是：a,b互质的充分必要条件是存在整数x,y使ax+by=1.

其实在高等代数的多项式部分有相关的定理、结论。

尝试dfs打表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
using namespace std;

bool dfs(int m,int p,int q){
    if (!m) return true;
    if (m >= p && dfs(m-p,p,q)) return true;
    if (m >= q && dfs(m-q,p,q)) return true;
    return false;
}
int main(){
    int p,q;
    cin >> p >> q;
    int res = 0;
    for (int i = 1;i <= 1000;i++){
        if (!dfs(i,p,q)) res = i;
        // res会不断更新到最大值
    }
    cout << res << endl;
    return 0;
}
/*
3 2 1
3 4 5
3 5 7
3 7 11
4 9 23
5 9 31
*/

m表示当前要凑的总数量，如果m == 0，就表示m已经被凑出来了，否则枚举当前选哪种糖，如果选p并且m - p可以被凑出来，那就是说明m可以被凑出；同理如果选q并且m - q可以被凑出来，那就说明m可以被凑出。

找规律：固定p不变，观察q变化时，答案怎么变化，再固定q不变，观察p变化时，答案怎么变化

1
2
3
4
5
6
7
8
2:n+2 m+2
3:n+1 m+2
4:n+2 m+6    3: m = 2n-3
                 1 = 2*2 + x x=-3   2n-3 = m
             4: m = 3n-4
             5: m = 4n-5
             p q
             ans = (q-1)p - q

找到规律直接给出代码：

1
2
3
4
5
6
7
8
9
10
// 证明比较复杂，以后可以当作结论直接记住
#include <iostream>
using namespace std;

int main(){
    int p,q;
    cin >> p >> q;
    cout << (p-1)*(q-1)-1;
    return 0;
}

总结：

引理：给定a，b，若d=gcd(a,b)>1,则一定不能凑出最大数。

结论：如果 a,b 均是正整数且互质，那么由 ax+by,x≥0,y≥0 不能凑出的最大数是 (a−1)(b−1)−1。

坚持原创技术分享，您的支持将鼓励我继续创作！