grant's Blog

记录生活中的点点滴滴

考研算法辅导课笔记（十四）

发表于 更新于 分类于 ， ，   阅读次数： Valine：
本文字数： 4.2k 阅读时长 ≈ 4 分钟

Insertion Sort（折半插入排序）

折半插入排序是对直接插入排序的简单优化。

算法思想：

直接插入排序直接线性查找到应插入位置，我们可以改进为通过二分查找到应插入位置。

这样做能减少比较次数，但不能减少移动次数。

代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 样例通过：10/13
#include <iostream>
using namespace std;
const int N = 100010;
int n,a[N];

void binary_search_insertion_sort(int a[],int l,int r){
    for (int i = l+1;i <= r;i ++){
        int temp = a[i]; // 二分查找有序部分中第一个大于temp的位置
        if (a[i-1] <= temp) continue; // 如果不存在，说明加上temp是有序的
        
        int st = l,ed = i-1;
        while (st < ed){
            int mid = st+ed >> 1;
            if (a[mid] > temp) ed = mid;
            else st = mid+1;
        }
        // st == ed就是第一个大于temp的位置
        // temp插入ed，a[ed~i-1]的元素向后挪动一位
        for (int j = i-1;j >= ed;j --)
            a[j+1] = a[j];
        a[ed] = temp;
    }
}

int main(){
    cin >> n;
    
    for (int i = 0;i < n;i ++) cin >> a[i];
    
    binary_search_insertion_sort(a,0,n-1);
    
    for (int i = 0;i < n;i ++) cout << a[i] << ' ';
    return 0;
}

效率分析：

和直接插入排序算法一致。

Bubble Sort（冒泡排序）

原理参考《排序算法：C++实现》。

算法思想：

  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

图片

代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

在朴素冒泡排序的基础上加了一个标志提前退出优化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 样例通过：10/13
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N],n;

void bubble_sort(int a[],int l,int r){
    bool flag = false;
    for (int i = l;i < r-l;i ++){ // 进行n-1轮冒泡
        for (int j = l;j + 1 <= r-i;j ++){
            if (a[j] > a[j+1]) // 每一轮冒泡确定一个最大的数，在数组右端
                swap(a[j],a[j+1]),flag = true;
        }
        if (!flag) break; // 如果本轮没有交换，说明已经有序
    }
}

int main(){
    cin >> n;
    
    for (int i = 0;i < n;i ++) cin >> a[i];
    
    bubble_sort(a,0,n-1);
    
    for (int i = 0;i < n;i ++) cout << a[i] << ' ';
    return 0;
}

效率分析：

1.最好时间复杂度：O(n)，已经有序。

如果要排序的数据已经是有序的，我们并不需要交换任何数据。第一轮冒泡遍历数组。

2.平均时间复杂度：$O(n^2)$。

两重for循环，平均是平方级别。

3.最坏时间复杂度：$O(n^2)$，倒序。

需要进行n-1轮冒泡，每一轮交换相邻元素，所以最坏情况时间复杂度为$O(n^2)$。

4.稳定性：稳定排序。

两个相等元素，是不会交换的，所以是稳定的。

Selection Sort（简单选择排序）

原理参考《排序算法：C++实现》。基本是最慢的排序。

算法思想：

  1. 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
  2. 从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾
  3. 以此类推，直到所有元素均排序完毕

图片

代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 样例通过：8/13
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N],n;

void selection_sort(int a[],int l,int r){
    for (int i = l;i <= r;i ++){
        int k = i; // 每轮循环找到未排序元素中的最小值
        for (int j = i + 1;j <= r;j ++){
            if (a[k] > a[j]) k = j;
        }
        swap(a[i],a[k]);
    }
}

int main(){
    cin >> n;
    
    for (int i = 0;i < n;i ++) cin >> a[i];
    
    selection_sort(a,0,n-1);
    
    for (int i = 0;i < n;i ++) cout << a[i] << ' ';
    return 0;
}

效率分析：

1.最好时间复杂度：$O(n^2)$。

2.平均时间复杂度：$O(n^2)$。

3.最坏时间复杂度：$O(n^2)$。

简单选择排序固定进行两轮循环，所以时间复杂度一定为$O(n^2)$。

4.稳定性：不稳定排序。

举个例子：排序2(1'),2(2'),1。第一轮后：1,2(2'),2(1')。

不稳定排序如何改进成稳定排序？

采用双关键字排序，第二个关键字取下标。

Shell Sort（希尔排序）

原理介绍：

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序。

本身并不复杂，但时间复杂度的证明比较麻烦。

算法思想：

  1. 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
  2. 按增量序列个数k，对序列进行k 趟排序；
  3. 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m的子序列，分别对各子表进行直接插入排序。仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。

图片

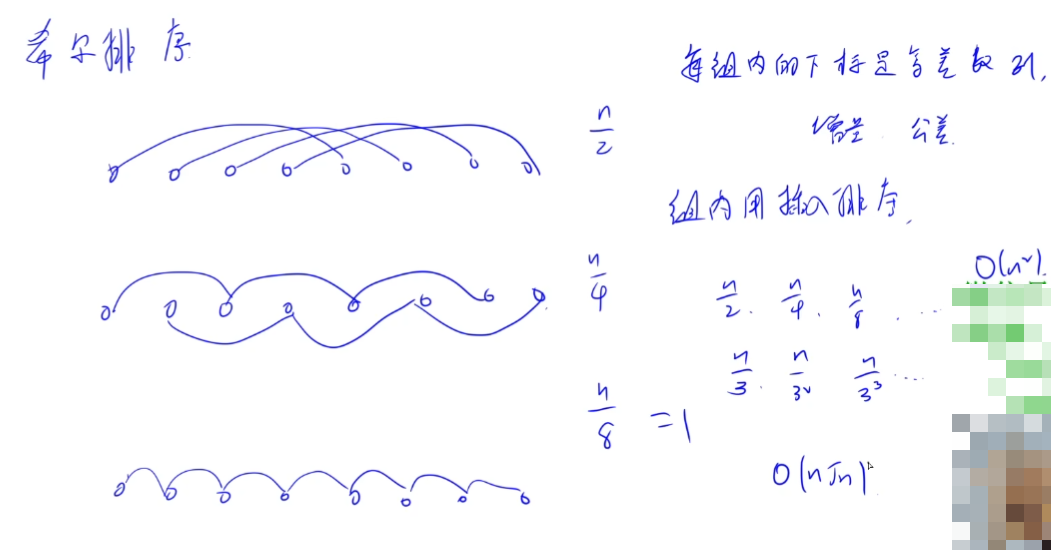
y总图解：

image-20220111203838458

每轮的增量可以自己随意选取，只要是逐渐减少的就行，还要保证最后一轮增量为1。

组内采用直接插入排序，因为直接插入排序对于部分有序的数组排序效率很高，有时比快排更快。

STL中的sort采用的就是快排和插排结合。

最后一轮公差为1，所有元素位于同一组，最终数组有序。

代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

从希尔排序开始可以AC。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// AC，样例通过：13/13
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N],n;

void shell_sort(int a[],int l,int r){
    int len = r-l+1;
    for (int d = len / 2; d; d /= 2){ // 枚举公差d
        // 效率改进：for (int d = len / 3; d;d = d == 2 ? 1 : d / 3)
        // 注意2/3下取整为0，要保证最后一轮公差为1
        for (int start = l;start < l+d;start ++){ // 将数组分为d组
            for (int i = start + d;i <= r;i += d){ // 组内相邻元素下标相差d，组内插排
                 // 指针i指向当前待插入元素，指针j从后往前扫描已有序部分
                int temp = a[i],j = i - d;
                while (j >= start && temp < a[j]){
                    a[j + d] = a[j];
                    j -= d;
                }
                a[j + d] = temp;
            }
        }
    }
}

int main(){
    cin >> n;
    
    for (int i = 0;i < n;i ++) cin >> a[i];
    
    shell_sort(a,0,n-1);
    
    for (int i = 0;i < n;i ++) cout << a[i] << ' ';
    return 0;
}

效率分析：

1.最好时间复杂度：O(n)。

2.平均时间复杂度：$O(n^{1.5})$。

每次公差缩小为原来的1/3。王道上写的是$O(n^{1.3})$。

3.最坏时间复杂度：$O(n^2)$。

4.稳定性：不稳定排序。

两个组前后交叉，假设两组有一个元素相等，后组的可能交换到前组的前面。

背下来就行。

坚持原创技术分享，您的支持将鼓励我继续创作！