grant's Blog

记录生活中的点点滴滴

考研算法辅导课笔记（十三）

发表于 更新于 分类于 ， ，   阅读次数： Valine：
本文字数： 4.3k 阅读时长 ≈ 4 分钟

字符串模式匹配（KMP）

KMP匹配算法的介绍参考算法基础课笔记（九）。

在字符串中查找子串：Knuth-Morris-Pratt 算法。KMP是比较难学的算法。

给定非空字符串s和p，其长度分别为n和m，为了便于讨论，将s称为主串（长文本），p称为模式串。

图解KMP算法：

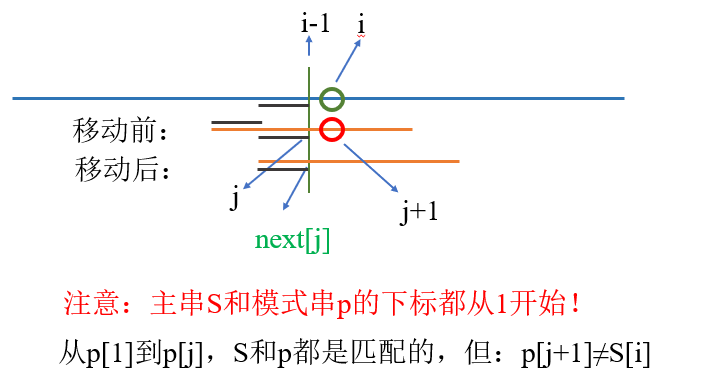
image-20210809072537893

acwing.831. KMP字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
给定一个模式串 S，以及一个模板串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。
模板串 P 在模式串 S 中多次作为子串出现。
求出模板串 P 在模式串 S 中所有出现的位置的起始下标。

输入格式
第一行输入整数 N，表示字符串 P 的长度。
第二行输入字符串 P。
第三行输入整数 M，表示字符串 S 的长度。
第四行输入字符串 S。

输出格式
共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围
1≤N≤10^5
1≤M≤10^6
输入样例：
3
aba
5
ababa
输出样例：
0 2

参考视频：原理讲解，代码讲解。

原理解析很清楚，有代码，非常棒！

视频中讲解了KMP算法中的next数组下标从0或者1开始的最长公共前后缀表。

注意：笔试要求计算KMP的比较次数时不要参考本题代码，代码中比较次数会更多，和手算不一致。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
using namespace std;
const int N = 1e5+5,M = 1e6+5;
int n,m;
int ne[N];
char p[N],s[M];

int main(){
    cin >> n >> p + 1; // 模板串，下标从1开始
    cin >> m >> s + 1; // 模式串，下标从1开始
    // 求模板串的prefix table，即前缀数组ne，模板串自己和自己匹配
    for (int i = 2,j = 0;i <= n;i ++){ // 默认ne[1] = 0，每轮循环求出ne[i]
        while (j && p[i] != p[j+1]) j = ne[j]; // i与j+1的位置比较
        if (p[i] == p[j+1]) j ++;
        ne[i] = j;
    }
    // KMP匹配过程
    for (int i = 1,j = 0;i <= m;i ++){
        while (j && s[i] != p[j+1]) j = ne[j]; // 失配则指针j回到ne[j]位置
        if (s[i] == p[j+1]) j ++;
        if (j == n){
            cout << i - n << ' '; // 题目定义下标从0开始，处理一下
            j = ne[j];
        }
    }
    return 0;
}

王道和教材中的KMP优化写法实际中几乎不会这样写，不需要掌握。

真题讲解

2011-9

image-20220101125229909

哈希表的存储效率指的是空间效率，也就是负载因子；查找效率指的是时间效率，也就是时间复杂度。

答案选B，因为三中“避免”二字太过绝对。（有点扯，笔试八股就这样）

2014-8

image-20220101125639473

哈希表的存储效率指的就是装填因子，就是存储的元素个数与哈希表大小之比，不受堆积现象影响。

答案选D。

2015-8

image-20220101130113497

手动模拟KMP匹配过程，注意串的下标从0开始！！！

image-20220101130611616

i = 5，j = 2。答案选C。

2018-9

image-20220101130745340

手动模拟闭散列方法（开放寻址法）。

每个关键字至少查找一次。

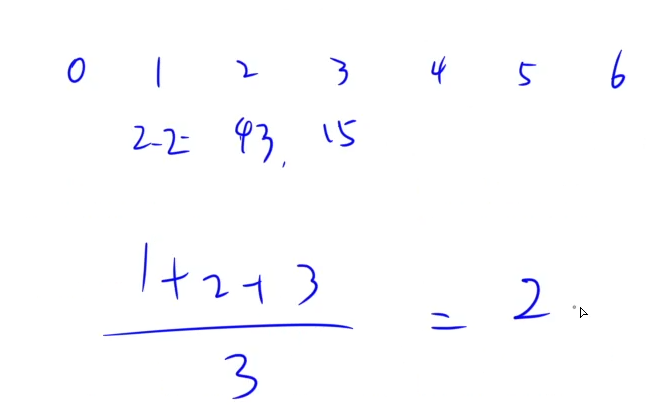
image-20220101131353750

答案选D。

2019-8

image-20220101131502360

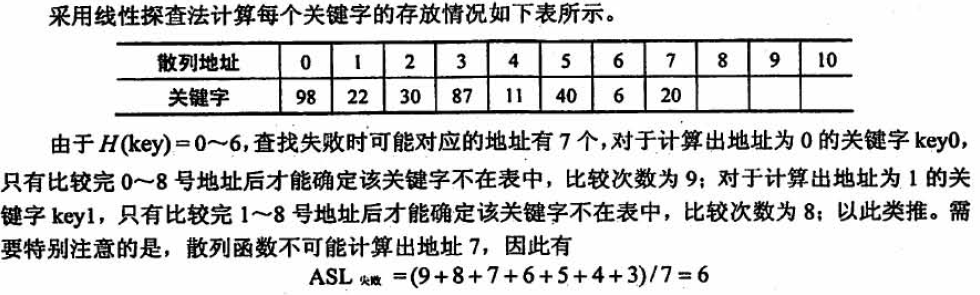
本题考察哈希表的查找失败的平均长度。注意一下。

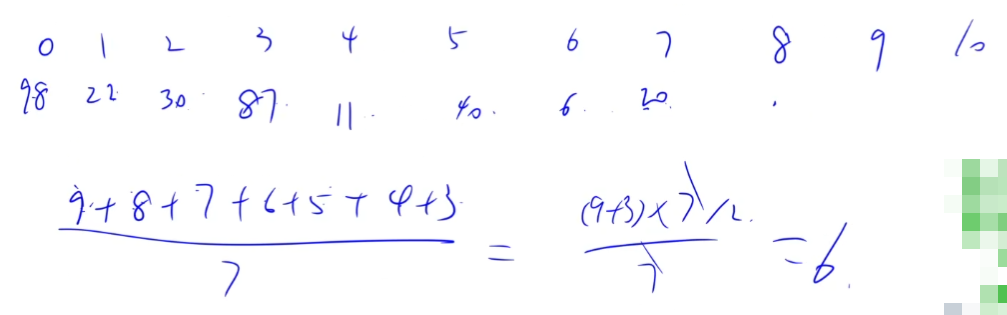
image-20220101132121019

答案选C。

image-20220101132243072

2019-9

image-20220101132321412

补充一个y总改进的求KMP单个字符的比较次数的程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
using namespace std;
const int N = 1e5+5,M = 1e6+5;
int n,m;
int ne[N];
char p[N],s[M];

int main(){
    cin >> n >> p + 1; // 模板串，下标从1开始
    cin >> m >> s + 1; // 模式串，下标从1开始
    // 求模板串的prefix table，即前缀数组ne，模板串自己和自己匹配
    for (int i = 2,j = 0;i <= n;i ++){ // 默认ne[1] = 0，每轮循环求出ne[i]
        while (j && p[i] != p[j+1]) j = ne[j]; // i与j+1的位置比较
        if (p[i] == p[j+1]) j ++;
        ne[i] = j;
    }
    // KMP匹配过程
    int cnt = 0; // 记录KMP单个字符的比较次数
    for (int i = 1,j = 0;i <= m;i ++){
        while (j){
            cnt ++;
            if (s[i] == p[j+1]) break;
            j = ne[j]; // 失配则指针j回到ne[j]位置
        }
        if (!j) cnt ++;
        if (s[i] == p[j+1]) j ++;
        if (j == n) break;
    }
    
    cout << cnt;
    return 0;
}
/*
输入：
6
abaabc
15
abaabaabcabaabc
输出：
10*/

手动模拟KMP匹配过程，计算比较次数。

答案选B。

第十一讲 基本概念、插入、冒泡、选择、希尔、快速、堆、归并排序

  1. 排序的基本概念
    (1) 内排序和外排序
    (2) 算法的稳定性
  2. 插入排序
    (1) 直接插入排序
     a. 时间复杂度
     [1] 最好情况：O(n)
     [2] 平均情况：O(n^2)
     [3] 最坏情况：O(n^2)
 b. 辅助空间复杂度
     O(1)
 c. 稳定
    (2) 折半插入排序
     a. 时间复杂度
     [1] 最好情况：O(n)
     [2] 平均情况：O(n^2)
     [3] 最坏情况：O(n^2)
 b. 辅助空间复杂度
     O(1)
 c. 稳定
  3. 冒泡排序（bubble sort）
    (1) 时间复杂度
     a. 最好情况：O(n)
 b. 平均情况：O(n^2)
 c. 最坏情况：O(n^2)
    (2) 空间复杂度
     O(1)
    (3) 稳定
  4. 简单选择排序
    (1) 时间复杂度
     a. 最好情况：O(n^2)
 b. 平均情况：O(n^2)
 c. 最坏情况：O(n^2)
    (2) 空间复杂度
     O(1)
    (3) 不稳定
  5. 希尔排序（shell sort）
    (1) 时间复杂度
     O(n^(3/2))
    (2) 空间复杂度
     O(1)
    (3) 不稳定
  6. 快速排序
    (1) 时间复杂度
     a. 最好情况：O(nlogn)
 b. 平均情况：O(nlogn)
 c. 最坏情况：O(n^2)
    (2) 空间复杂度
     O(logn)
    (3) 不稳定
  7. 堆排序
    (1) 时间复杂度
     a. 最好情况：O(nlogn)
 b. 平均情况：O(nlogn)
 c. 最坏情况：O(nlogn)
    (2) 空间复杂度
     O(logn)
    (3) 不稳定
  8. 二路归并排序（merge sort）
    (1) 时间复杂度
     a. 最好情况：O(nlogn)
 b. 平均情况：O(nlogn)
 c. 最坏情况：O(nlogn)
    (2) 空间复杂度
     O(n)
    (3) 稳定

完整系统的竞赛排序相关知识可以参考： https://oi-wiki.org/basic/sort-intro/。

Insertion Sort（直接插入排序）

原理参考《排序算法：C++实现》。

算法思想：

  1. 从第一个元素开始，该元素可以认为已经被排序
  2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
  3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
  4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
  5. 将新元素插入到该位置后
  6. 重复步骤2~5

图片

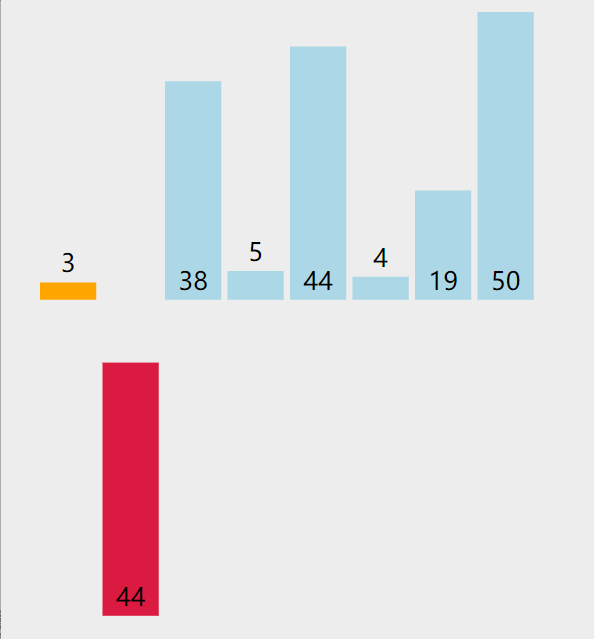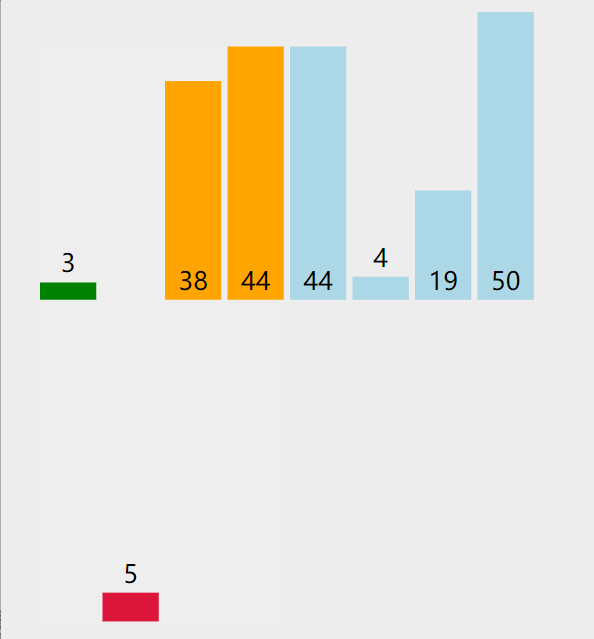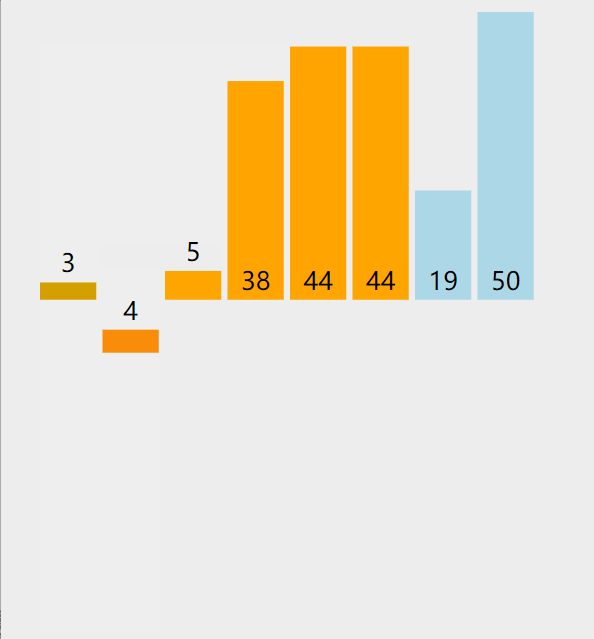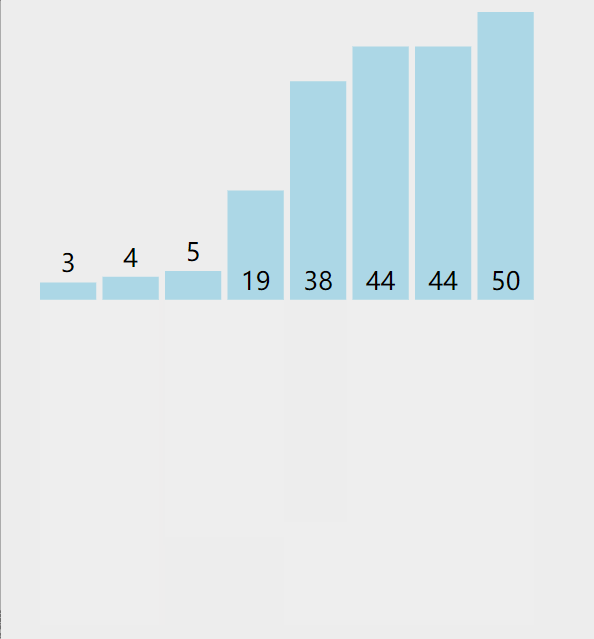
插入排序就类似打扑克抓牌。

插入排序将数组分成已排序和未排序两个部分，过程就是将待插入元素插入如有序部分。这里的做法是从后往前枚举有序部分来确定插入位置。

代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 样例通过：10/13
#include <iostream>
using namespace std;
const int N = 100010;
int n,a[N];

void insertion_sort(int a[],int l,int r){
    for (int i = l+1;i <= r;i ++){ // 双指针扫描数组
        int temp = a[i],j = i-1; // 指针i指向当前待插入元素，指针j从后往前扫描已有序部分
        while (j >= l && temp < a[j]){ // temp应当插入的位置就是temp >= a[j]的位置
            a[j+1] = a[j]; // 比temp大的元素向后挪一位
            j--; // 指针j向前移动
        }
        a[j+1] = temp; // 找到temp应当插入的位置
    }
}

int main(){
    cin >> n;
    
    for (int i = 0;i < n;i ++) cin >> a[i];
    
    insertion_sort(a,0,n-1);
    
    for (int i = 0;i < n;i ++) cout << a[i] << ' ';
    return 0;
}

效率分析：

1.最好时间复杂度：O(n)，已经有序。

如果要排序的数据已经是有序的，我们并不需要搬移任何数据。如果我们从尾到头在有序数据组里面查找插入位置，每次只需要比较一个数据就能确定插入的位置。所以这种情况下，最好是时间复杂度为 O(n)。注意，这里是从尾到头遍历已经有序的数据。

2.平均时间复杂度：$O(n^2)$。

还记得我们在数组中插入一个数据的平均时间复杂度是多少吗？没错，是 O(n)（平均来说在每个位置插入概率相等）。所以，对于插入排序来说，每次插入操作都相当于在数组中插入一个数据，循环执行 n 次插入操作，所以平均时间复杂度为$O(n^2)$。

3.最坏时间复杂度：$O(n^2)$，倒序。

如果数组是倒序的，每次插入都相当于在数组的第一个位置插入新的数据，所以需要移动大量的数据，所以最坏情况时间复杂度为$O(n^2)$。

4.稳定性：稳定排序。

假设有序部分元素为：1,2,4,6，现在插入2，从后往前找到第一个2 >= a[j]的位置j，有序部分中的2肯定还在前面，所以是稳定的。

十大经典排序算法大梳理 (动图+代码)

各类排序算法的复杂度及稳定性总结：

1.png

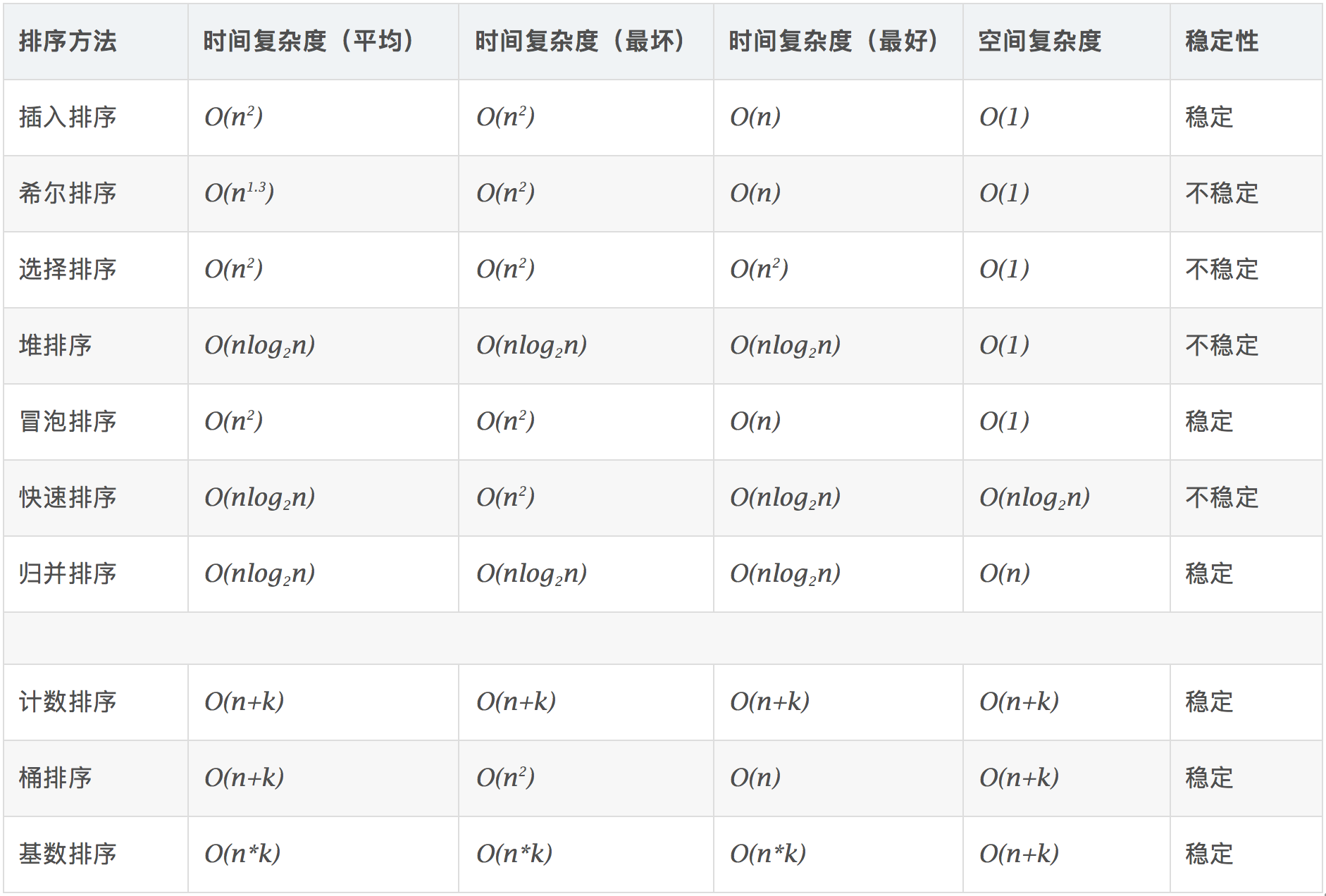
注：快排的时间复杂度是O(logn)，上图中标错了。

坚持原创技术分享，您的支持将鼓励我继续创作！