蓝桥杯学习总结（二五）

七树状数组、线段树与差分

之前我们先学习了双指针、宽搜，跳过了本章内容，现在补上。

树状数组与线段树是两种比较特殊的数据结构。

本章内容难度比较高，但在蓝桥杯中考察最基本应用，涉及也较少。

邱秋老师的《Programming Challenges》对大部分数据结构都有详细的介绍。

胡凡的《算法笔记》也介绍了树状数组。

1.树状数组

树状数组，又称二叉索引树（binary index tree），简称BIT，是一个多叉树。

树状数组是一个查询和修改复杂度都为log(n)的数据结构。它支持修改，是一个在线做法。

主要用于给某个位置上的数加上一个数和快速求前缀和。（单点修改和区间查询）

前缀和只能查询，复杂度为O(1)，但是不支持修改。修改的话要重新计算前缀和，平均需要O(n)时间。

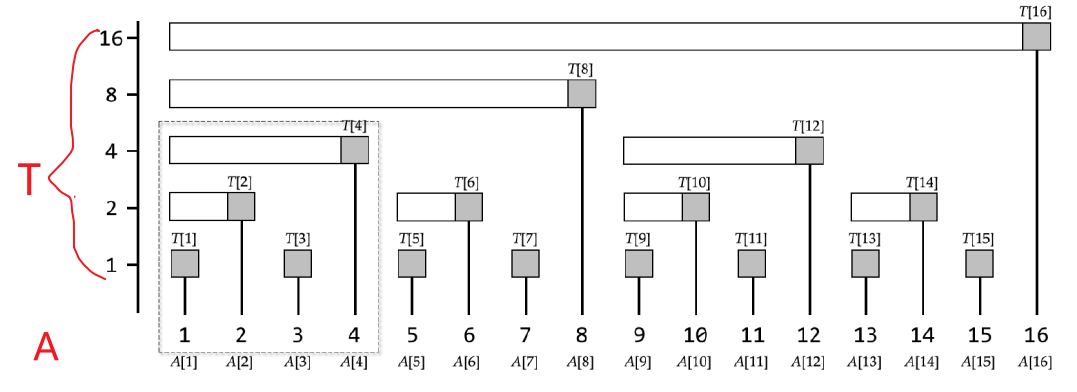
树状数组的定义：树状数组是一维的！！！

其中横坐标为数组A元素的序号x（从1开始计数），纵坐标为lowbit(x)。

inline int lowbit(int x) { return x & (-x); }

lowbit(x)就是取x的二进制最右边的1和它右边所有0。右边有k个0表示在第k层。

例如，十进制数40的二进制表示为101000，lowbit($40_{10}$)＝$1000_{2}$=8。

所以：核心点，T[x] = sum(x-2^k,x] = sum(x-lowbit(x),x]。（左开右闭）

// 返回前x个数之和:a[1]+a[2]+...+a[x]
// 时间复杂度：O(logn)
int getSum(int x){
    int res = 0;
    for (int i = x;i > 0;i -= lowbit(i)) res += t[i];
    return res;
}

// 将a[x] + v
// 时间复杂度：O(logn)
// 记住！！！
void update(int x,int v){
    for (int i = x;i <= n;i += lowbit(i)) t[i] += v;
}

以上两个函数就是BIT最核心的内容，可以解决一系列问题。

1.1 acwing.1264. 动态求连续区间和

《信息学奥赛一本通》,模板题

给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b] 的连续和。

输入格式
第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。
第二行包含 n 个整数，表示完整数列。
接下来 m 行，每行包含三个整数 k,a,b （k=0，表示求子数列[a,b]的和；k=1，表示第 a 个数加 b）。
数列从 1 开始计数。

输出格式
输出若干行数字，表示 k=0 时，对应的子数列 [a,b] 的连续和。

数据范围
1≤n≤100000,
1≤m≤100000，
1≤a≤b≤n
输入样例：
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例：
11
30
35

思路：

模板题，直接套用上面讲的理论。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 100010;

int a[N],tr[N];
int n,m;
int lowbit(int x){// 三个核心函数都得背过
    return x & -x;
}

void update(int x,int v){// add()，加数
    for (int i = x;i <= n;i += lowbit(i)) tr[i] += v;
}

int getSum(int x){// query()，查询
    int res = 0;
    for (int i = x;i;i -= lowbit(i)) res += tr[i];
    return res;
}
int main(){
    scanf("%d%d",&n,&m);
    for (int i = 1;i <= n;i++) scanf("%d",&a[i]);
    for (int i = 1;i <= n;i++) update(i,a[i]);// 初始化树状数组
    
    while (m--){
        int k,x,y;
        scanf("%d%d%d",&k,&x,&y);
        if (k == 0) printf("%d\n",getSum(y) - getSum(x-1));
        else update(x,y);
    }
    
    return 0;
}

1.2 acwing.1265. 数星星

《信息学奥赛一本通》 , Ural 1028

天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。

如果一个星星的左下方（包含正左和正下）有 k 颗星星，就说这颗星星是 k 级的。

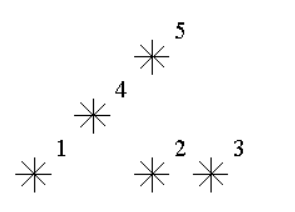
例如，上图中星星 5 是 3 级的（1,2,4 在它左下），星星 2,4 是 1级的。

例图中有 1个 0 级，2个 1 级，1 个 2 级，1 个 3 级的星星。

给定星星的位置，输出各级星星的数目。

换句话说，给定 N 个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

输入格式
第一行一个整数 N，表示星星的数目；
接下来 N 行给出每颗星星的坐标，坐标用两个整数 x,y 表示；
不会有星星重叠。星星按 y 坐标增序给出，y 坐标相同的按 x 坐标增序给出。

输出格式
N 行，每行一个整数，分别是 0 级，1 级，2 级，……，N−1 级的星星的数目。

数据范围
1≤N≤15000,
0≤x,y≤32000
输入样例：
5
1 1
5 1
7 1
3 3
5 5
输出样例：
1
2
1
1
0

思路：

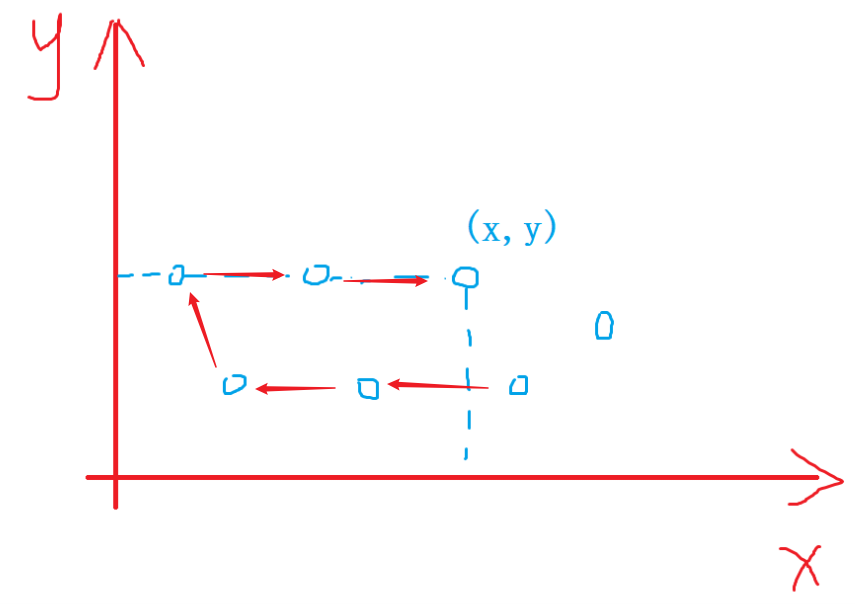
题目要求求某一个点(x,y)左下方星星的个数(不包括自己)，且星星按y坐标增序给出，y 坐标相同的按x坐标增序给出,因此对于每个新来的点(x,y),y是当前纵坐标的最大值，只需要求[1,x]中星星出现的数量即可，利用前缀和。

注意：本题给出的星星坐标是按照纵坐标增序的，所以后面给出的星星横坐标可能比前面给出的要小，所以必

须更新前缀和数组，就必须用到树状数组了，实现在线查询。

不包括自己，而计算前缀和会加进去，注意审题。

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 32010;
int n;
int tr[N],level[N];

int lowbit(int x){
    return x & -x;
}

void add(int x,int v){// 注意：不要写成i <= n，因为x可能>n
    for (int i = x;i <= N;i += lowbit(i)) tr[i] += v;
}

int query(int x){
    int res = 0;
    for (int i = x;i;i -= lowbit(i)) res += tr[i];
    return res; 
}

int main(){
    scanf("%d",&n);
    for (int i = 1;i <= n;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        x++;// 细节，前缀和数组从1开始，题目x>=0
        // 注意：求左下方星星数目时，自己也会包含进去，但题目要求不包含
		// 所以先查询前缀和，再插入点
        level[query(x)] ++;// 统计左下方星星数为x的星星+1
        add(x,1);// 将横坐标为x的星星+1
    }

    for (int i = 0;i < n;i++) printf("%d\n",level[i]);
    
    return 0;
}

七 树状数组、线段树与差分

1.树状数组

1.1 acwing.1264. 动态求连续区间和

1.2 acwing.1265. 数星星

七树状数组、线段树与差分