grant's Blog

记录生活中的点点滴滴

蓝桥杯学习总结（二六）

发表于 更新于 分类于 ，   阅读次数： Valine：
本文字数： 4.8k 阅读时长 ≈ 4 分钟

2.线段树

线段树（segment tree）是一种以二叉树为基础的数据结构，可以用于进行高效的范围最大（小）值查询、范围和查询等。

原理比树状数组要简单，但是代码更复杂。

推荐文章1：https://www.acwing.com/blog/content/372/。

推荐文章2：https://www.acwing.com/blog/content/392/。

推荐文章3：https://blog.csdn.net/weixin_43914593/article/details/108221534。

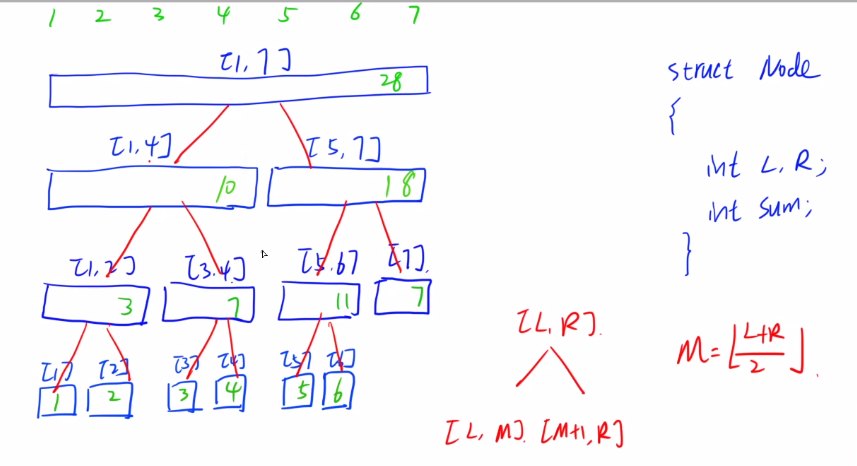
线段树,树上面的所有节点都是线段,都是一个区间.

在构建线段树之前，我们先阐述线段树的性质：

1、线段树的每个节点都代表一个区间。

2、线段树具有唯一的根节点，代表的区间是整个统计范围，如[1,N]。

3、线段树的每个叶节点都代表一个长度为1的元区间[x,x]。

4、对于每个内部节点[l,r]，它的左子结点是[l,mid]，右子节点是[mid+1,r]，其中mid=(l+r)/2（向下取整）。

以结点node的性质为sum为例，构建线段树：

image-20210607133844216

在声明空间时，一般以查询区间长度的4倍来申请存储空间较为“安全”。（结点总数<=4*叶子结点数）

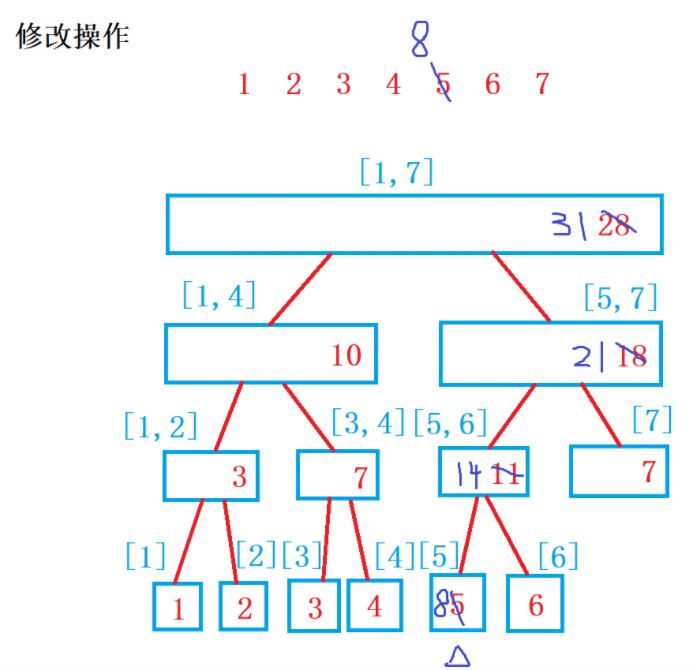
操作1：单点修改，更新指定值的叶子结点，同时更新它的所有祖先结点。O(logn).

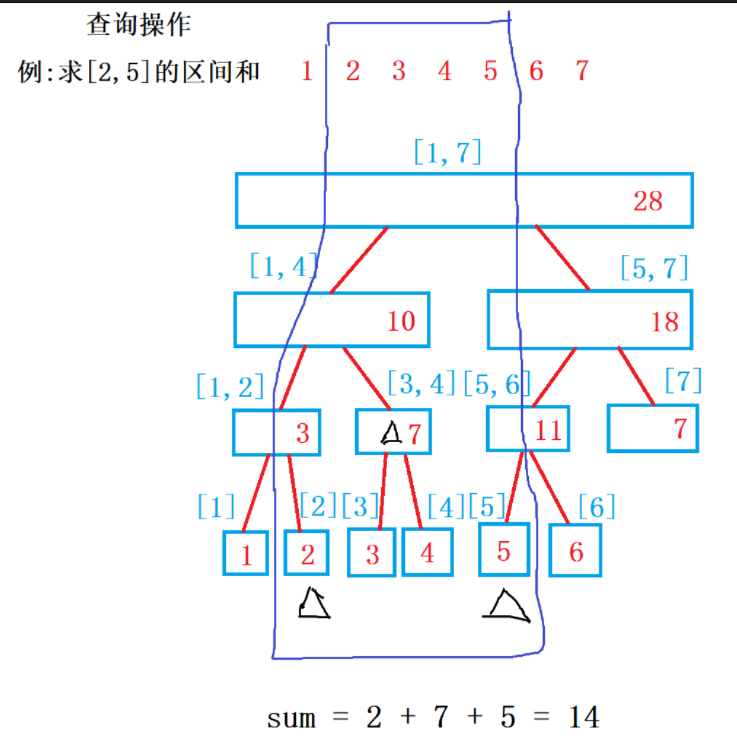
操作2：区间查询，对于给定区间，不断二分递归，直到子区间将给定区间完全包含，再合并。O(logn).

对于区间修改操作，需要用到懒惰标记（lazy tag），会使得线段树的难度陡增，这里就不讨论。

四个核心函数：

image-20210607145648848

image-20210607150248115

图解修改操作：

image-20210607160405433

图解查询操作：

image-20210607160429723

2.1 acwing.1264. 动态求连续区间和

上一讲树状数组的模板题。

线段树写法。比树状数组稍慢一点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;

const int N = 100010;
struct Node{// 线段树结点
    int l,r;// 左孩子和右孩子
    int sum;// 结点性质为求和
}tr[N*4];
int n,m;
int w[N];

void pushup(int u){// 用子结点更新当前结点的sum，上传操作，把信息往上传递
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void build(int u,int l,int r){
    if (l == r) tr[u] = {l,r,w[r]};// 叶子结点
    else{
        tr[u] = {l,r};// 初始化左右端点
        int mid = l + r >> 1;// 递归左孩子和右孩子
        build(u << 1,l,mid),build(u << 1 | 1,mid+1,r);
        pushup(u);// 更新当前结点的sum
    }
}

int query(int u,int l,int r){
    // 给定查询区间完全包含线段树结点的区间，可以直接计算
    if (l <= tr[u].l && r >= tr[u].r) return tr[u].sum;
    int sum = 0;
    // 否则二分处理
    int mid = tr[u].l + tr[u].r >> 1;
    if (l <= mid) sum += query(u << 1,l,r);// 说明与左孩子有交集
    if (r > mid) sum += query(u << 1 | 1,l,r);// 即r>=mid+1，说明与右孩子有交集
    return sum;
}

void modify(int u,int x,int v){
    if (tr[u].l == tr[u].r) tr[u].sum += v;// 叶子结点，目标位置
    else{
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1,x,v);
        else modify(u << 1 | 1,x,v);
        pushup(u);// 回溯时更新当前结点的sum
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for (int i = 1;i <= n;i++) scanf("%d",&w[i]);
    build(1,1,n);// 初始化线段树，下标从1开始
    while (m--){
        int k,a,b;
        scanf("%d%d%d",&k,&a,&b);
        if (k == 0) printf("%d\n",query(1,a,b));
        else modify(1,a,b);
    }
    return 0;
}

2.2 acwing.1270. 数列区间最大值

《信息学奥赛一本通》

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
输入一串数字，给你 M 个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。

输入格式
第一行两个整数 N,M 表示数字的个数和要询问的次数；
接下来一行为 N 个数；
接下来 M 行，每行都有两个整数 X,Y。

输出格式
输出共 M 行，每行输出一个数。

数据范围
1≤N≤10^5,
1≤M≤10^6,
1≤X≤Y≤N,
数列中的数字均不超过2^31−1
输入样例：
10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8
输出样例：
5
8

思路：

维护区间的最大值。这种问题可以归结为RMQ，即询问区间最值。

只要将上一题结点性质由求和改为最大值就行。

代码：

题解1：线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <climits>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 1e5+10;
int n,m;
int w[N];
struct Node{
  int l,r;
  int maxv;// 结点性质为最大值
}tr[N*4];

void build(int u,int l,int r){
    if (l == r) tr[u] = {l,r,w[r]};
    else{
        tr[u] = {l,r};
        int mid = l + r >> 1;
        build(u << 1,l,mid),build(u << 1 | 1,mid+1,r);
        tr[u].maxv = max(tr[u << 1].maxv,tr[u << 1 | 1].maxv);// 更新结点最大值
    }
}

int query(int u,int l,int r){
    if (l <= tr[u].l && r >= tr[u].r) return tr[u].maxv;
    int res = INT_MIN;// 定义在<climits>头文件
    int mid = tr[u].l + tr[u].r >> 1;
    if (l <= mid) res = query(u << 1,l,r);// 可以不用和res取max
    if (r > mid) res = max(res,query(u << 1 | 1,l,r));// 下面必须取max
    return res;
}

int main(){
    scanf("%d%d",&n,&m);
    for (int i = 1;i <= n;i++) scanf("%d",&w[i]);
    build(1,1,n);
    
    int a,b;
    while (m--){
        scanf("%d%d",&a,&b);
        printf("%d\n",query(1,a,b));
    }
    return 0;
}

题解2：树状数组求区间最值，本题的树状数组解法和hdu1754比较像。

参考1（思路）：https://www.cnblogs.com/liyexin/p/12877821.html

参考2（代码）：https://www.acwing.com/solution/content/25010/

直接照搬求区间合的方法显然是不行的。

因为区间合中，要查询[x,y]的区间合，是求出[1,x-1]的合与[1,y]的和，然后相减就得出了[x,y]区间的和。

而区间最值是没有这个性质的，所以只能够换一个思路。

我们从右往左查询，对于r来讲，它所管辖的有lowbit(r)个区间。所以对于[l,r]如果r-l>=lowbit(r)，那么tr[r]可

以直接拿来用，因为tr[x]表示的是tree[x-lowbit(x)+1,x]的最大值，在范围内。而如果lowbit(r)超出了[l,r]，那

么就r—对L进行逼近，直到满足r-l>=lowbit(r)进入上面的操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <climits>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e5+10;

int n,m;
int tr[N];
int a[N];

int lowbit(int x){
    return x & -x;
}

void modify(int x,int v){// 更新tr数组最大值
    for (int i = x;i <= N;i += lowbit(i)) tr[i] = max(tr[i],v);
}

int query(int l,int r){// 查询区间[l,r]的最大值
    int res = INT_MIN;
    while (l <= r){
        res = max(res,a[r--]);// 指针r从右往左查询，直到r-l>lowbit(r)进入循环
        for (;r-l > lowbit(r);r -= lowbit(r)) res = max(res,tr[r]);// 换成r-l >= lowbit(r)也行
    }
    return res;
}
int main(){
    scanf("%d%d",&n,&m);
    for (int i = 1;i <= n;i++){
        scanf("%d",&a[i]);
        modify(i,a[i]);// 边读入边处理
    }
    
    int a,b;
    while (m--){
        scanf("%d%d",&a,&b);
        printf("%d\n",query(a,b));
    }
    return 0;
}
坚持原创技术分享，您的支持将鼓励我继续创作！