考研算法辅导课笔记（十一）

第九讲 基本概念、顺序、折半、分块查找法、B/B+树

1. 查找的基本概念
   (1) 平均查找长度 ASL = 每个元素 查找概率 * 找到第i个元素需要进行的比较次数 的和。
   (2) 决策树(判定树)
2. 顺序查找法
   (1) 一般线性表的顺序查找

    a. 若每个元素查找概率相同，则 ASL(成功) = (1 + 2 + ... + n) / n = (n + 1) / 2
    b. ASL(失败) = n或n+1，取决于代码写法。
   

   (2) 有序表的顺序查找

    a. 若每个元素查找概率相同，则 ASL(成功) = (1 + 2 + ... + n) / n = (n + 1) / 2
    b. ASL(失败) = (1 + 2 + ... + n + n) / (n + 1) = n / 2 + n / (n + 1)
   

3. 折半查找法
   (1) ASL(成功) = log(n + 1) - 1
4. 分块查找法
   设共n个元素，每块s个元素，共b = n / s块。块内无序，块间有序。
   (1) 顺序查找确定块：ASL(成功) = (s^2 + 2s + n) / (2s)，s = sqrt(n)时取最小值
   (2) 二分查找确定块：log(n/s + 1) + (s - 1)/2

---

详细的概念知识和查找代码实现参考王道P257。

平均查找长度 ASL = 每个元素 查找概率 * 找到第i个元素需要进行的比较次数 的和。

一般认为每个元素 查找概率相等，为1/n。

平均查找长度 ASL分为两种，ASL（成功）和ASL（失败）。

ASL（失败）中每个元素在一个区间查找失败的概率就是1/(n+1)，n+1是区间的个数。

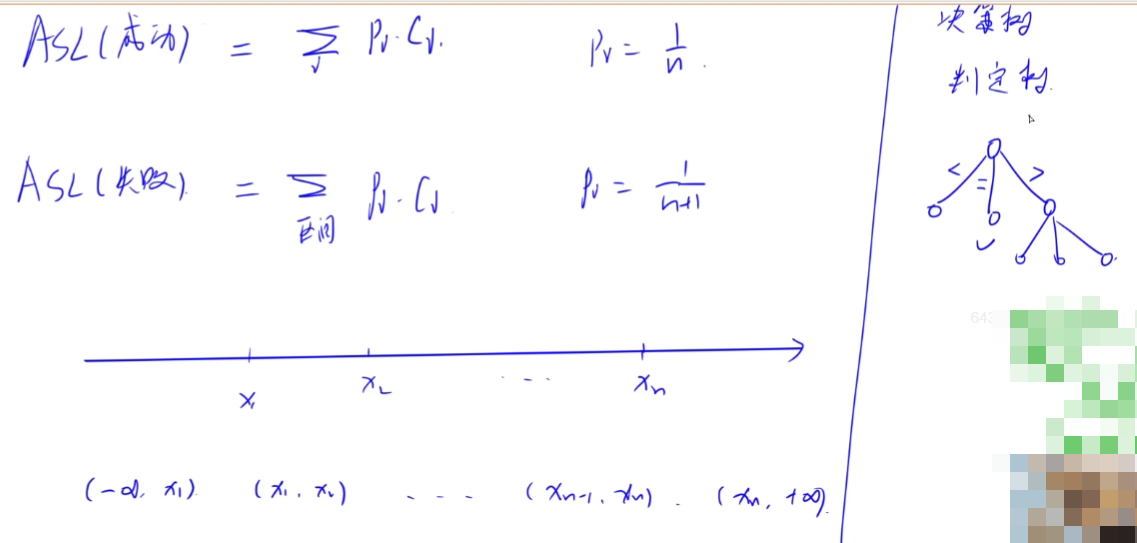
顺序（线性）查找

1.一般线性表的顺序查找

查找成功的ASL如下图：

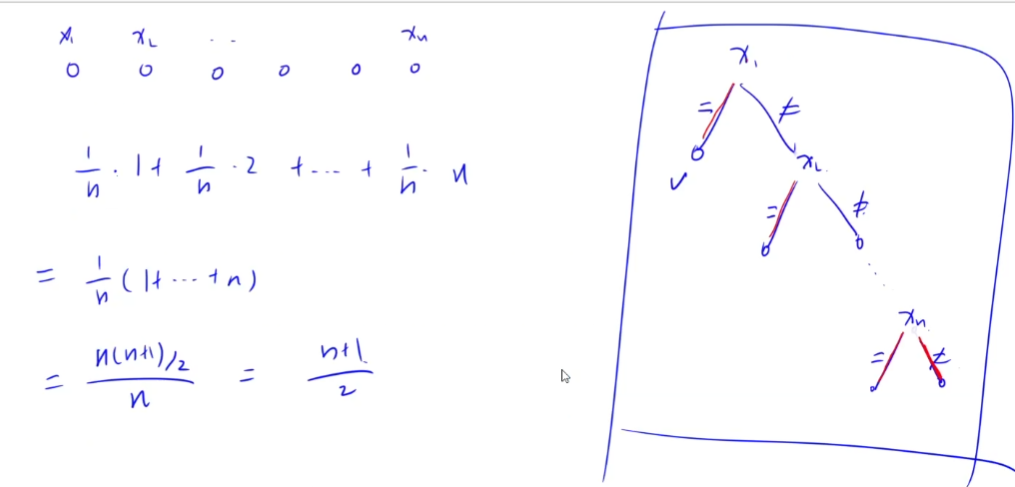
ASL(失败) = n或n+1。

查找失败也就是一直往右走的分支，需要比较n次，有的教材（王道等）写的是n+1次，取决于代码写法，按照王道的写法就是n+1次，不用纠结，考试不会为难。

下面附上王道的伪代码写法：

int search_Seq(int ST[],int key){
    ST[0] = key; // ST[0]作为哨兵，存放待查找的关键字
    for (int i = ST.size()-1;ST[i] != key; --i); // 从后往前查找
    return i; // 查找成功：返回位置i；查找失败：返回哨兵位置0，比较n+1次
}

2.有序表的顺序查找

判定树如下图所示：

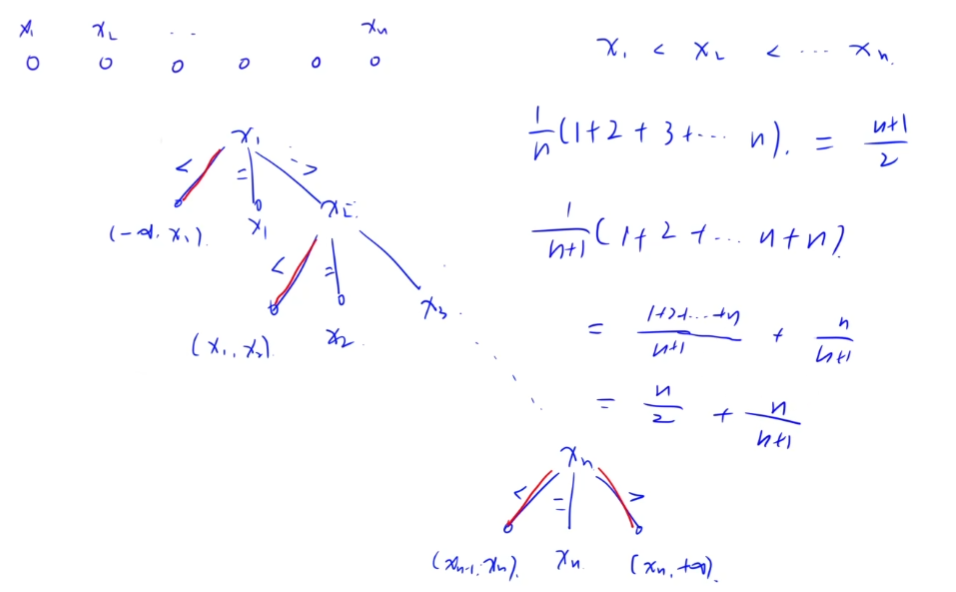
ASL(成功) = (1 + 2 + … + n) / n = (n + 1) / 2，查找成功对应每个取等号的分支。

ASL(失败) = (1 + 2 + … + n + n) / (n + 1) = n / 2 + n / (n + 1)，查找失败对应红色的分支，n个节点有n+1个失败分支，括号里的是每个失败分支的比较次数，第n个和第n+1个失败分支的比较次数都是n次。

折半（二分）查找

注意区别笔试的二分写法和机试的二分写法！

折半查找的分界点有下取整和上取整两种方式。

按王道教材写法，每次比较分了三种情况。

下面附上王道的伪代码写法：

int binary_Search(int L[],int key){
    int low = 0,high = L.size()-1,mid;
    while (low <= high){
        mid = (low+high)/2; // 408也会考察上取整写法
        if (L[mid] == key) return mid; // 查找成功：返回mid
        else if (L[mid] > key) high = mid - 1;
        else low = mid + 1;
    }
    return -1; // 查找失败：返回-1
}

判定树如下图所示：

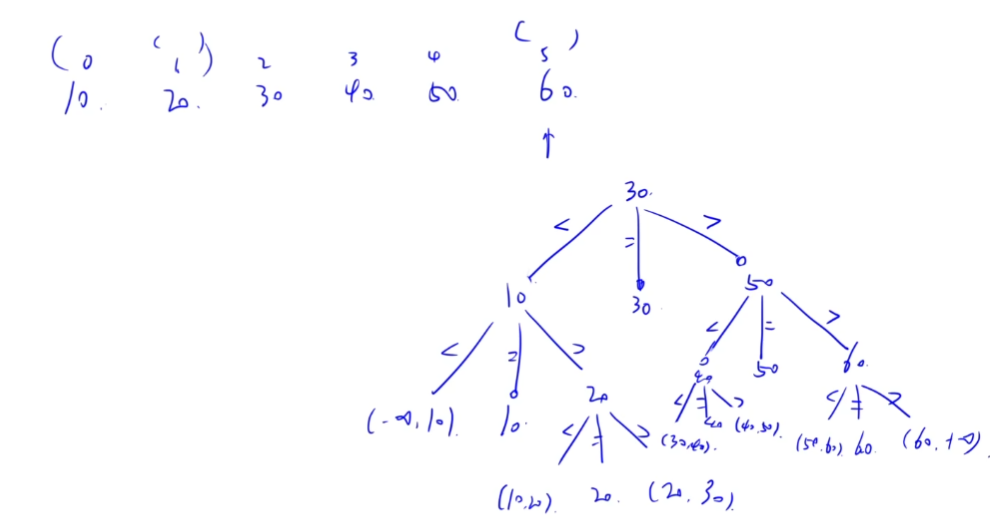
容易发现二分查找的判定树就是一棵平衡的二叉排序树，中序序列有序。

ASL(成功) = log(n + 1) - 1。（近似结论）

如果有像上图的具体示例，ASL(成功)可以直接算出来。

这里ASL的计算看王道P261描述得更准确。

分块（索引顺序）查找

将查找表分为若干子块，块内元素无序，块间元素有序。

设共n个元素，每块s个元素，共b = n / s块。块内无序，块间有序。

(1) 顺序查找确定块：ASL(成功) = (s^2 + 2s + n) / (2s)，s = sqrt(n)时取最小值

(2) 二分查找确定块：log(n/s + 1) + (s - 1)/2

顺序查找：先确定在哪块（有序表的顺序查找），然后块内查找（一般线性表的顺序查找）。

两步的ASL(成功)都是(n+1)/2。所以整体：ASL(成功) = (b+1)/2 + (s+1)/2 = (s^2 + 2s + n) / (2s)。

二分查找：先确定在哪块（二分查找），然后块内查找（一般线性表的顺序查找）。

整体：ASL(成功) = log(b+1)-1 + (s+1)/2 = log(n/s + 1) + (s - 1)/2。

B/B+树

B树及其基本操作、B+树及其基本概念
(1) B树
	[1] m阶B树，每个节点最多有m个孩子。
	[2] 每个节点最多有m-1个关键字（可以存有的键值对）。
	[3] 根节点最少可以只有1个关键字，也就是说至少有2棵子树。
	[4] 非根节点至少有ceil(m/2)-1个关键字。（ceil：上取整）
	[5] 每个节点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
	[6] 所有叶子节点都位于同一层，或者说根节点到每个叶子节点的长度都相同。
	[7] 每个节点都存有索引和数据，也就是对应的key和value。
	[8] 所以，根节点的关键字数量范围：1 <= k <= m-1，非根节点的关键字数量范围：ceil(m/2)-1 <= k <= m-1。
(2) B+树
	[1] B+跟B树不同，B+树的非叶子节点不保存关键字记录的指针，只进行数据索引，这样使得B+树每个非叶子节点所能保存的关键字大大增加；
	[2] B+树叶子节点保存了父节点的所有关键字记录的指针，所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样；
	[3] B+树叶子节点的关键字从小到大有序排列，左边结尾数据都会保存右边节点开始数据的指针。

---

B/B+树在算法中不常用到，主要在操作系统，数据库等地方的查找用到。

B树和B+树的插入、删除图文详解；b-树b+树_图解；

邓俊辉数据结构：B树；数据结构与算法之美专栏；王道教材P270。

邓老师的讲解是很不错的！y总的讲解也很精彩！

408考研重在考察B树，对B+树只考察基本概念。

B/B+树是对BST（二叉搜索树）的拓展。

对于B/B+树的定义最好以王道为准，不同地方定义不同。

---

B树也称B-树（这不是减号）,它是一颗所有节点的平衡因子均等于0的多路平衡查找树。我们描述一颗B树时需要指定它的阶数，阶数表示了一个结点最多有多少个孩子结点，一般用字母m表示阶数。当m取2时，就是我们常见的二叉搜索树。

B树图示：

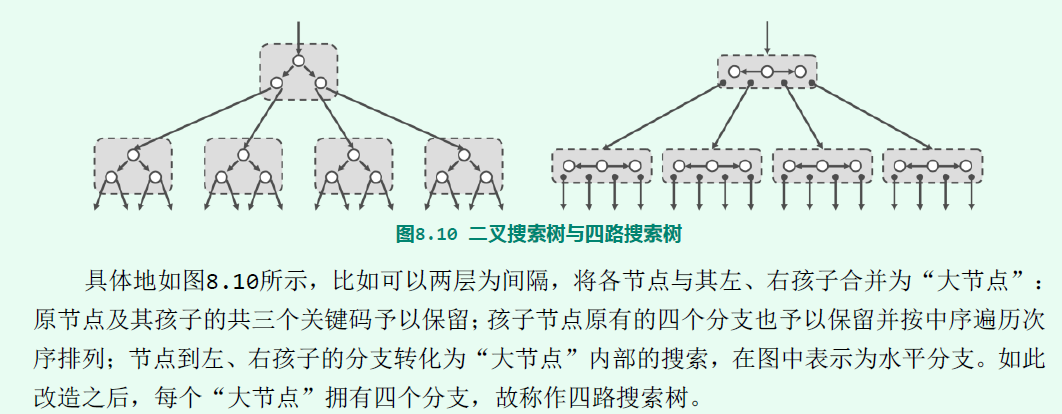
上图中，灰色的节点称为内部节点，最底层的叶子节点（上图没画出来）称为外部节点。

y总图解：

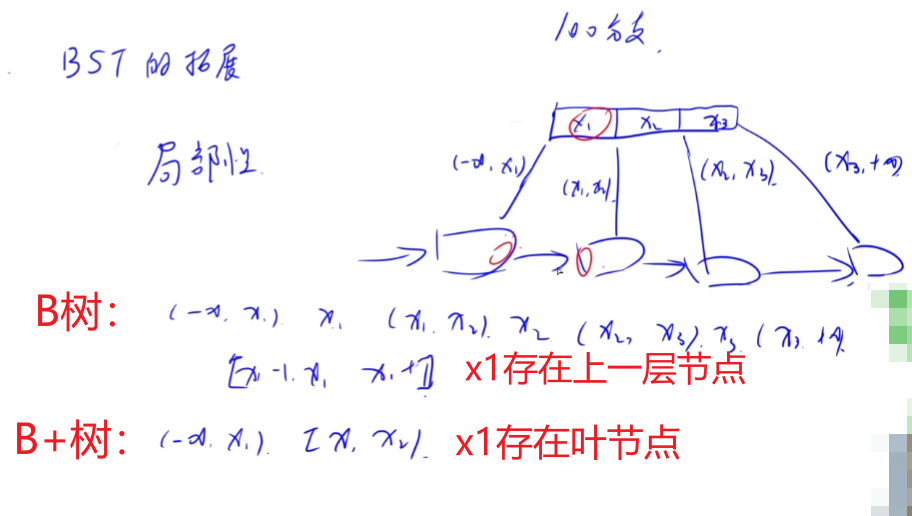
上图中B+树相比B树还会将在最底层的叶子节点通过链表串联起来，方便查找。

B+树比B树的局部性更好，也就是说在B+树中，几个连续节点存放的位置也是连续的。

以[x1-1,x1,x1+1]为例，B树需要在下层查找2次，上层查找1次；而B+树只需要在下层查找2次。

B 树实际上是低级版的 B+ 树，或者说 B+ 树是 B 树的改进版。

B 树跟 B+ 树的不同点主要集中在这几个地方：B+ 树中的节点不存储数据，只是索引，而 B 树中的节点存储数据；B 树中的叶子节点并不需要链表来串联。

---

B树的相关操作：

B树查找，类似折半查找。

B树插入

插入操作是指插入一条记录，即（key, value）的键值对。如果B树中已存在需要插入的键值对，则用需要插入的value替换旧的value。若B树不存在这个key,则一定是在叶子结点中进行插入操作。

1）根据要插入的key的值，找到叶子结点并插入。

2）判断当前结点key的个数是否小于等于m-1，若满足则结束，否则进行第3步。

3）以结点中间的key为中心分裂成左右两部分，然后将这个中间的key插入到父结点中，这个key的左子树指向分裂后的左半部分，这个key的右子支指向分裂后的右半部分，然后将当前结点指向父结点，继续进行第3步。

看上面第一篇博客模拟一遍就会了，或者参考王道P272页。画图注意下箭头指向的位置。

B树删除

删除操作要比插入复杂一点。

删除操作是指，根据key删除记录，如果B树中的记录中不存对应key的记录，则删除失败。

1）如果当前需要删除的key位于非叶子结点上，则用后继key（这里的后继key均指后继记录的意思）覆盖要删除的key，然后在后继key所在的子支中删除该后继key。此时后继key一定位于叶子结点上，这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步

2）该结点key个数大于等于ceil(m/2)-1，结束删除操作，否则执行第3步。

3）如果兄弟结点key个数大于ceil(m/2)-1，则父结点中的key下移到该结点，兄弟结点中的一个key上移，删除操作结束。

否则，将父结点中的key下移与当前结点及它的兄弟结点中的key合并，形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针，指向这个新结点。然后当前结点的指针指向父结点，重复上第2步。

有些结点它可能即有左兄弟，又有右兄弟，那么我们任意选择一个兄弟结点进行操作即可。

---

B+树

[1] m阶B+树，每个节点最多有m个孩子。
[2] 每个节点最多有m个关键字（可以存有的键值对）。
[3] 节点的子树个数与关键字个数相等。
[4] 所以，非根节点的关键字数量范围：ceil(m/2) <= k <= m。
[5] 根节点最少可以有2棵子树。
[6] 每个节点中的关键字都按照从小到大的顺序排列，每个关键字对应的子树中的所有关键字都小于等于它。

B+树的操作与B树类似，只是查找操作稍有区别。

拓展内容，B/B+树的实际应用：

为了节省内存，如果把树存储在硬盘中，那么每个节点的读取（或者访问），都对应一次磁盘 IO 操作。树的高度就等于每次查询数据时磁盘 IO 操作的次数。

比起内存读写操作，磁盘 IO 操作非常耗时，所以我们优化的重点就是尽量减少磁盘 IO 操作，也就是，尽量降低树的高度。

想要进一步了解B树在操作系统的应用可以参考《算法导论》第五章高级数据结构。