grant's Blog

记录生活中的点点滴滴

考研算法辅导课笔记（十二）

发表于 更新于 分类于 ， ，   阅读次数： Valine：
本文字数： 4.6k 阅读时长 ≈ 4 分钟

真题讲解

2011-42

image-20211225212950832

参考答案：

leetcode-cn—4. 寻找两个正序数组的中位数

有兴趣可以尝试，leetcode上的题和本题稍有区别，难度为困难，细节很多。

题解一：暴力合并两个数组，再计算中位数。时间复杂度：O(m+n)，空间复杂度：O(m+n)。

题解二：二分查找，分情况讨论，代码细节多，但笔试不要求能运行。时间复杂度：O(log(m+n))，空间复杂度：O(1)。

要找到中位数，不一定要合并两数组然后计算。

只要保证中位数的左右两边的数的个数一样就可以。

二分思路如下：

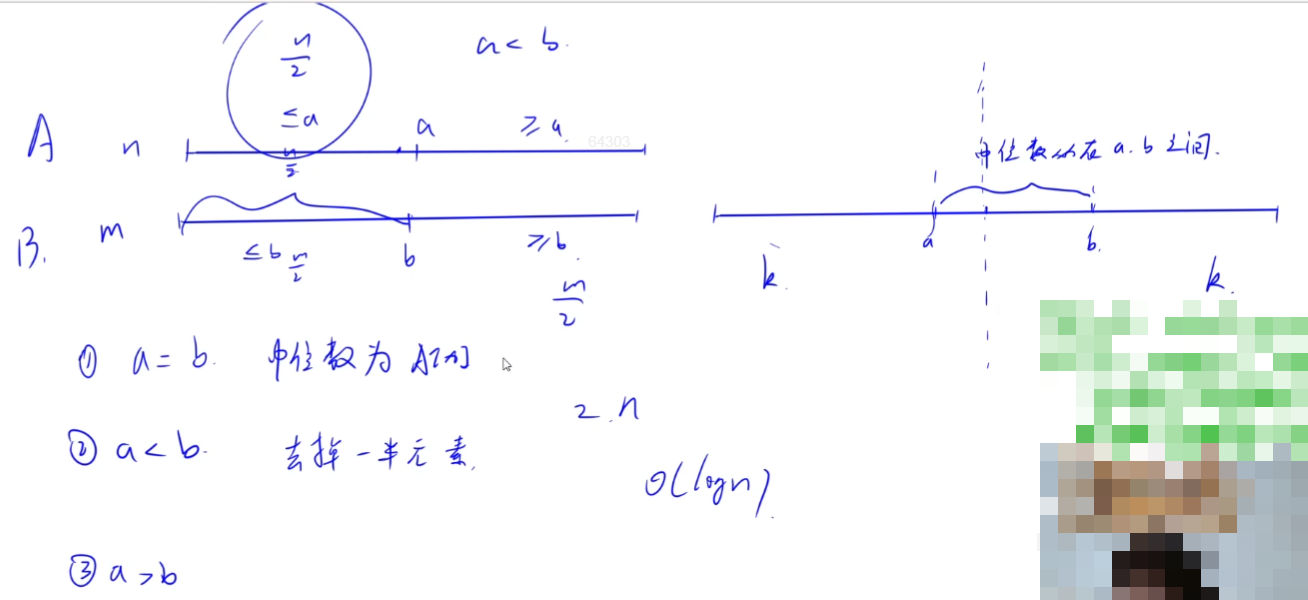
image-20211225220033567

每次执行二分时分为三种情况：

  1. 两序列的中位数相等，a == b，那么a就是两序列的中位数；
  2. a < b，那么就是两序列的中位数一定位于a和b之间，两序列各去掉自己的一半元素；
  3. a > b，那么就是两序列的中位数一定位于a和b之间，两序列各去掉自己的一半元素。

所以，重复下去直到第一种情况出现，就找到了两序列的中位数。

考试考到只能暴力骗分了。

2012-9

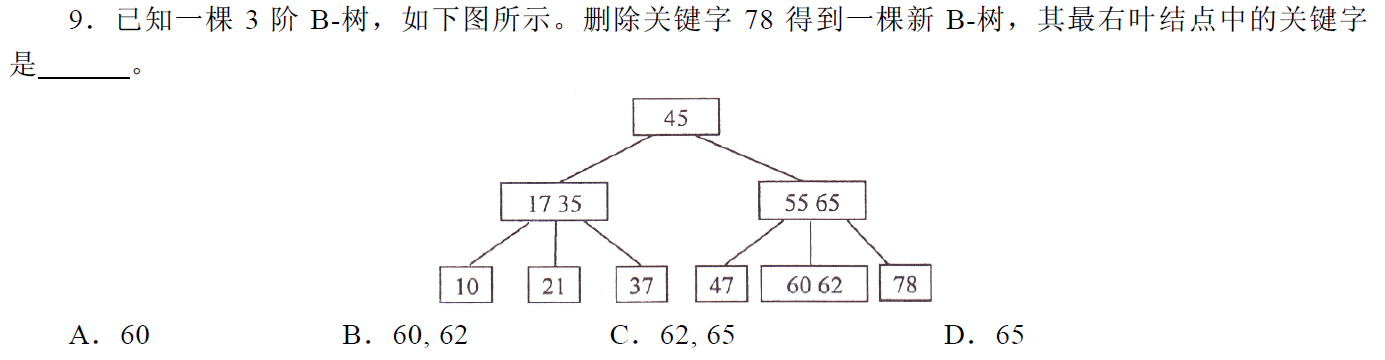
image-20211225221721812

回顾一下B树的知识点：

  • m阶B树，每个节点最多有m个孩子。

  • 每个节点最多有m-1个关键字（可以存有的键值对）。

  • 非根节点至少有ceil(m/2)-1个关键字。（ceil：上取整）

3阶B-树，非根非叶节点关键字个数为1到2个。

删掉78之后，右子树不足1个关键字，而左子树有2个关键字，所以从左边借一个。

左子树的62转到父节点，然后父节点的65转到右子树。类似AVL右旋。

答案选D。

2013-10

image-20211225222642126

根节点至少有2棵子树，也就是1个关键字。每棵子树，至少有2个关键字。

总共是5个关键字。

答案选A。

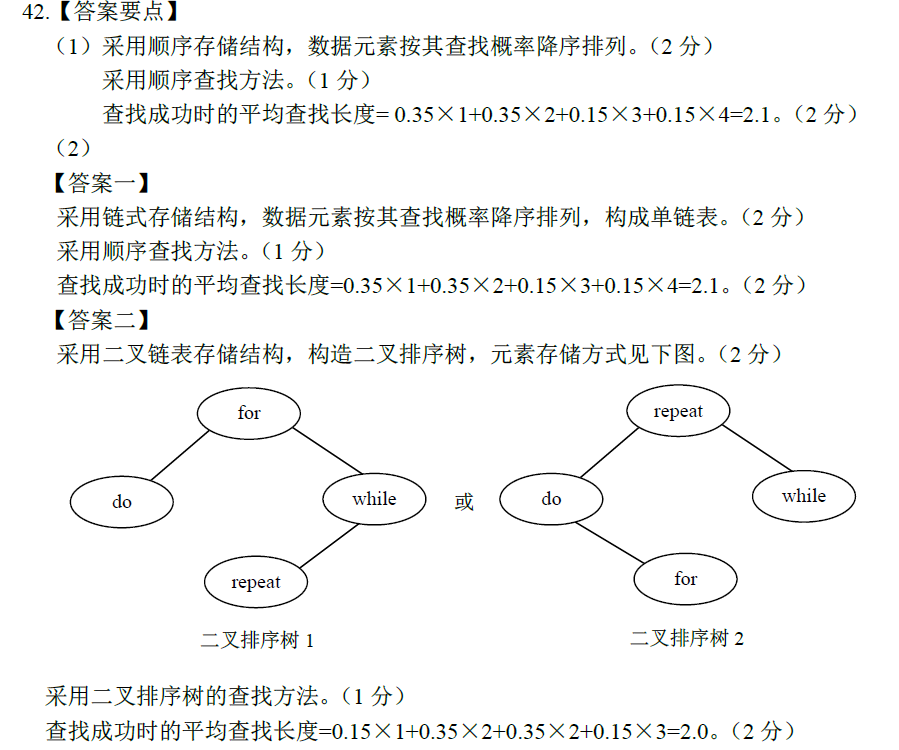
2013-42

image-20211226155408073

折半查找法，如果不说明默认下取整折半。

（1）顺序查找，查找概率最大的放最前面。

（2）链式查找，就是利用链表，树和图的结构查找。考察二叉排序树。

注意这里不要把哈夫曼树和二叉排序树搞混！

哈夫曼树是最佳归并树，用于合并操作；二叉排序树用于搜索和查找。

二叉排序树（BST）的中序序列是一个有序序列。

这里使用单链表和BST都能拿满分。

参考答案：

image-20211226161214047

2014-9

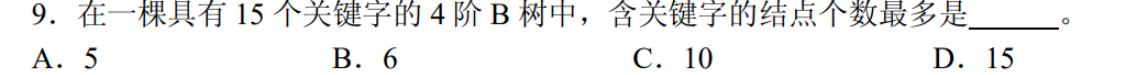
image-20211226161342106

每个非根非叶节点至少含有1个关键字，根节点至少含有1个关键字。

15个关键字对应15个节点。

答案选D。

2015-7

image-20211226161914577

做法：根据选项中的序列构造出一棵BST，看看中序序列是否有序。

答案选A。

2016-9

image-20211226162724036

A：本算法查找n/3次，二分查找logn次；B：本算法查找约3次，二分查找logn次；

C：本算法查找n/3次，二分查找logn次；D：看成n/2个数的结尾，本算法查找约n/6次，二分查找1次。

以上计算只是近似计算，并不准确。

答案选B。

2016-10

image-20211226162745515

考察B/B+树的基本概念。

答案选A。

2017-8

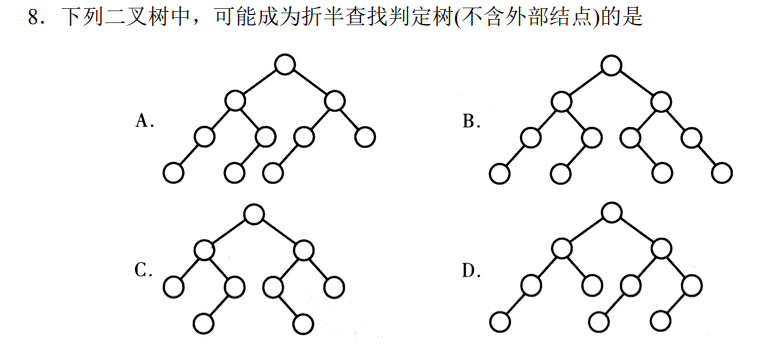
image-20211226165002479

容易发现二分查找的判定树就是一棵平衡的二叉排序树，中序序列有序。

给每棵树的节点按中序编号，看看是否符合二分查找。

如何判定？二分判定树要么全部符合上取整规则，要么都是下取整规则，如果矛盾说明不是二分判定树。

参考答案如下：

image-20211226170000285

2017-9

image-20211226170336982

A，C都是在内存中查找，D中磁盘空闲块用链表维护起始结束位置，不会存入整个块的位置信息。

答案选B。

2018-8

image-20211226170656971

每个非根非叶节点至少含有1个关键字，根节点至少含有1个关键字。

每个节点至少有2个孩子。高度为5层，总共31个孩子。

答案选B。

2020-10

image-20211226171029562

模拟B树的插入操作。

每个非根非叶节点包含的关键字数量为1到3个。

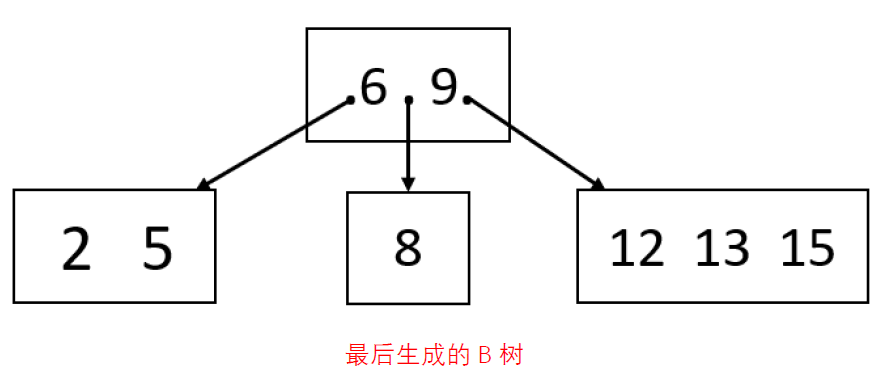
image-20211226171527675

生成的B-树并不唯一，但根节点的关键字是一样的。

如果插入节点需要将多余节点向上提时，且是偶数个节点，优先提靠右节点。

第十讲 散列（Hash）表、字符串模式匹配（KMP）

  1. 散列（Hash）表
    (1) 负载因子
    (2) 哈希函数
     [1] 除余法 h(x) = x % M
 [2] 乘余取整法 h(x) = floor(n * (A * x的小数部分))
 [3] 平方取中法 先平方，然后取中间几位
 [4] 基数转换法 换成其他进制，然后取其中几位
 [5] ELFhash字符串
    (3) 解决冲突的方式
     [1] 开散列方法（拉链法）
 [2] 闭散列方法（开放寻址法）
     聚集和二级聚集
     a. 线性探查法 d(i) = (d(0) + i * c) % M。易产生聚集问题。
     b. 二次探查法。易产生二级聚集问题。
         d(2i - 1) = (d(0) + i^2) % M
         d(2i) = (d(0) -  i^2) % M
     c. 随机探查法。易产生二级聚集问题。
     d. 双散列探查法

散列（Hash）表

参考王道P281。

负载因子（装填因子）：等于 已有元素数/散列表长度。

常用的散列（哈希）函数：

1
2
3
4
5
[1] 除余法 h(x) = x % M
[2] 乘余取整法 h(x) = floor(n * (A * x的小数部分)), 0 < A < 1
[3] 平方取中法 先平方，然后取中间几位
[4] 基数转换法 换成其他进制，然后取其中几位
[5] ELFhash字符串

解决冲突的方式：代码以及题解参考，蓝桥杯学习总结（四十）

[1] 开散列方法（拉链法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int h[N], e[N], ne[N], idx;
// 向哈希表中插入一个数
void insert(int x)
{
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++ ;
}

// 在哈希表中查询某个数是否存在
bool find(int x)
{
    int k = (x % N + N) % N;
    for (int i = h[k]; i != -1; i = ne[i])
        if (e[i] == x)
            return true;

    return false;
}

[2] 闭散列方法（开放寻址法）

根据处理冲突的方式又分为四种方式：

1
2
3
4
5
6
a. 线性探查法 d(i) = (d(0) + i * c) % M。易产生聚集问题。
b. 二次探查法。易产生二级聚集问题。
    d(2i - 1) = (d(0) + i^2) % M
    d(2i) = (d(0) - i^2) % M
c. 随机探查法，伪随机序列法。易产生二级聚集问题。
d. 双散列探查法

开放寻址法的其中一种写法： 线性探查法。

1
2
3
4
5
6
7
8
9
10
11
12
  int h[N];
// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
int find(int x)
{
    int t = (x % N + N) % N;
    while (h[t] != null && h[t] != x)
    {
        t ++ ;
        if (t == N) t = 0;
    }
    return t;
}

acwing.840. 模拟散列表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
维护一个集合，支持如下几种操作：
I x，插入一个数 x；
Q x，询问数 x 是否在集合中出现过；
现在要进行 N 次操作，对于每个询问操作输出对应的结果。

输入格式
第一行包含整数 N，表示操作数量。
接下来 N 行，每行包含一个操作指令，操作指令为 I x，Q x 中的一种。

输出格式
对于每个询问指令 Q x，输出一个询问结果，如果 x 在集合中出现过，则输出 Yes，否则输出 No。
每个结果占一行。

数据范围
1≤N≤10^5
−10^9≤x≤10^9
输入样例：
5
I 1
I 2
I 3
Q 2
Q 5
输出样例：
Yes
No

[1] 开散列方法（拉链法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5+5,M = 100003;
int h[N],e[N],ne[N],idx;

void add(int x,int y){
    e[idx] = y;
    ne[idx] = h[x];
    h[x] = idx ++;
}

bool find(int x){
    int t = (x%M + M)%M;
    for (int i = h[t]; ~i;i = ne[i])
        if (e[i] == x) return true;
    return false;
}

void insert(int x){
    int t = (x%M + M)%M;
    add(t,x);
}

int main(){
    int n,x;
    string op;
    cin >> n;
    
    memset(h,-1,sizeof h);
    while (n--){
        cin >> op >> x;
        if (op == "I") insert(x);
        else if (op == "Q"){
            if (find(x)) cout << "Yes\n";
            else cout << "No\n";
        }
    }
    return 0;
}

[2] 闭散列方法（开放寻址法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 200003,null = 0x3f3f3f3f;
int h[N];

int find(int x){
    int t = (x % N + N) % N;
    while (h[t] != null && h[t] != x) t = (t+1)%N;
    return t;
}

int main(){
    int n,x;
    string op;
    cin >> n;
    
    memset(h,0x3f,sizeof h);
    while (n--){
        cin >> op >> x;
        int k = find(x);
        if (op == "I") h[k] = x;
        else if (op == "Q"){
            if (h[k] == x) cout << "Yes\n";
            else cout << "No\n";
        }
    }
    return 0;
}

acwing.3820. 未出现过的最小正整数（2018年408）

给定一个长度为 n 的整数数组，请你找出未在数组中出现过的最小正整数。

样例：

1
2
3
4
5
6
7
输入1：[-5, 3, 2, 3]

输出1：1

输入2：[1, 2, 3]

输出2：4

数据范围：

1≤n≤10^5,

数组中元素的取值范围 [−10^9,10^9]。

思路：

显然我们可以从小到大枚举找到未出现过的最小正整数。

当1~n中有数没有出现时，就找到了答案；若1~n中所有数都出现了，答案就是n+1。

所以本题并不需要哈希表，只要开一个大小为n+1的数组就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findMissMin(vector<int>& nums) {
        int n = nums.size();
        vector<bool> hash(n+1);
        
        for (int num : nums){
            if (num >= 1 && num <= n) hash[num] = true;
        }
        
        for (int i = 1;i <= n;i ++){
            if (!hash[i]) return i;
        }
        return n+1;
    }
};
坚持原创技术分享，您的支持将鼓励我继续创作！