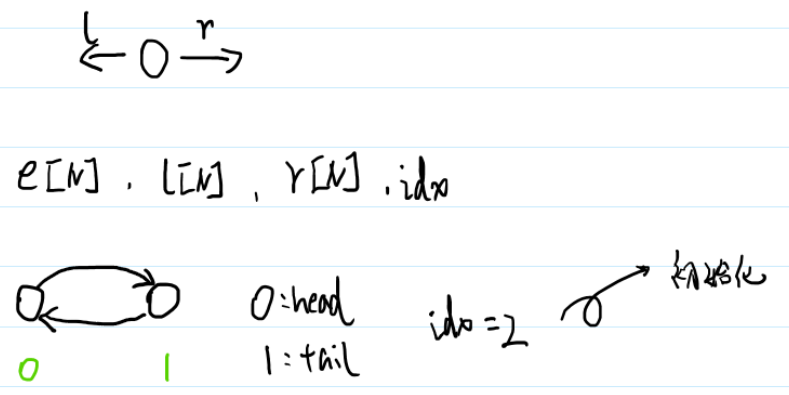算法基础课笔记（七）

二：数据结构

第二章：数据结构模板整理， https://www.acwing.com/blog/content/404/

2.1：链表、栈与队列

数组模拟单链表。应用：邻接表，常用于存储树、图。

在蓝桥杯（二一）详细介绍过数组模拟单链表。

为什么用数组模拟？

因为算法上指针+结构体的效率较低，慢。

例题：826. 单链表（模板题）

实现一个单链表，链表初始为空，支持三种操作：
向链表头插入一个数；
删除第 k 个插入的数后面的数；
在第 k 个插入的数后插入一个数。
现在要对该链表进行 M 次操作，进行完所有操作后，从头到尾输出整个链表。
注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

输入格式
第一行包含整数 M，表示操作次数。
接下来 M 行，每行包含一个操作命令，操作命令可能为以下几种：
H x，表示向链表头插入一个数 x。
D k，表示删除第 k 个插入的数后面的数（当 k 为 0 时，表示删除头结点）。
I k x，表示在第 k 个插入的数后面插入一个数 x（此操作中 k 均大于 0）。

输出格式
共一行，将整个链表从头到尾输出。

数据范围
1≤M≤100000
所有操作保证合法。

输入样例：
10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6
输出样例：
6 4 6 5

题解1：y总代码。

#include <iostream>
using namespace std;

const int N = 100010;

int e[N],ne[N];
int head,idx;

void init(){
    head = -1;
    // idx = 0;
}
// 头插法
void add_to_head(int x){
    e[idx] = x,ne[idx] = head,head = idx++;// 最后一步等价于: head = idx,idx++;
}
// 将x插入下标是k的结点之后
void add(int k,int x){
    e[idx] = x,ne[idx] = ne[k],ne[k] = idx++;
}
// 将下标为k的结点的后一个结点删除
void remove(int k){// k = 0在后面会特殊处理
    ne[k] = ne[ne[k]];
}

int main(){
    ios::sync_with_stdio(false);

    init();
    int m;cin >> m;
    
    char op;
    int x1,x2;
    while (m--){
        cin >> op;// 使用cin避免了读入换行符的问题
        if (op == 'H'){
            cin >> x1;
            add_to_head(x1);
        }
        if (op == 'D'){
            cin >> x1;
            if (!x1) head = ne[head];// 删除头结点
            else remove(x1-1);
        }
        if (op == 'I'){
            cin >> x1 >> x2;
            add(x1-1,x2);
        }
    }
    for (int i = head;i != -1;i = ne[i]) cout << e[i] << " ";    
    
    return 0;
}

注意：本题的头结点指的是第一个插入的结点，head即为头结点的下标。head是头指针，不是头结点。

第k个插入的数，也就是下标（idx）为k-1的数。

使用头插法得到的序列：head—>k—>k-1—>…—>1—>0—>-1。

注意：当 k 为 0 时，表示删除头结点。

特别注意：如果用scanf输入会读入末尾的回车符，需要在读入k和x时处理，scanf("%d\n",xxx);

题解2：idx初始化为1，让位置0作为头结点，这样就可以把所有操作统一了。

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int cur=1, e[N], ne[N];

void add_k(int k, int x)
{
    e[cur] = x; ne[cur] = ne[k]; ne[k] = cur++;
}

void del_k(int k)
{
    ne[k] = ne[ne[k]];
}


int main()
{
    int m; cin >> m;
    while (m--) {
        char op; int k,x;
        cin >> op;
        if (op == 'H') {
            cin >> x;
            add_k(0,x);
        } else if (op == 'I') {
            cin >> k >> x;
            add_k(k,x); 
        } else {
            cin >> k;
            del_k(k);
        }
    }

    for (int j = ne[0]; j ; j = ne[j]) cout << e[j] << ' ';
    cout << endl;
    return 0;
}

数组模拟双链表。应用：优化某些问题。

例题：827. 双链表（模板题）

实现一个双链表，双链表初始为空，支持 5 种操作：
在最左侧插入一个数；
在最右侧插入一个数；
将第 k 个插入的数删除；
在第 k 个插入的数左侧插入一个数；
在第 k 个插入的数右侧插入一个数
现在要对该链表进行 M 次操作，进行完所有操作后，从左到右输出整个链表。
注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

输入格式
第一行包含整数 M，表示操作次数。
接下来 M 行，每行包含一个操作命令，操作命令可能为以下几种：
L x，表示在链表的最左端插入数 x。
R x，表示在链表的最右端插入数 x。
D k，表示将第 k 个插入的数删除。
IL k x，表示在第 k 个插入的数左侧插入一个数。
IR k x，表示在第 k 个插入的数右侧插入一个数。
    
输出格式
共一行，将整个链表从左到右输出。

数据范围
1≤M≤100000
所有操作保证合法。

输入样例：
10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2
输出样例：
8 7 7 3 2 9

参考题解： https://www.acwing.com/solution/content/5052/。

初始化双向链表：

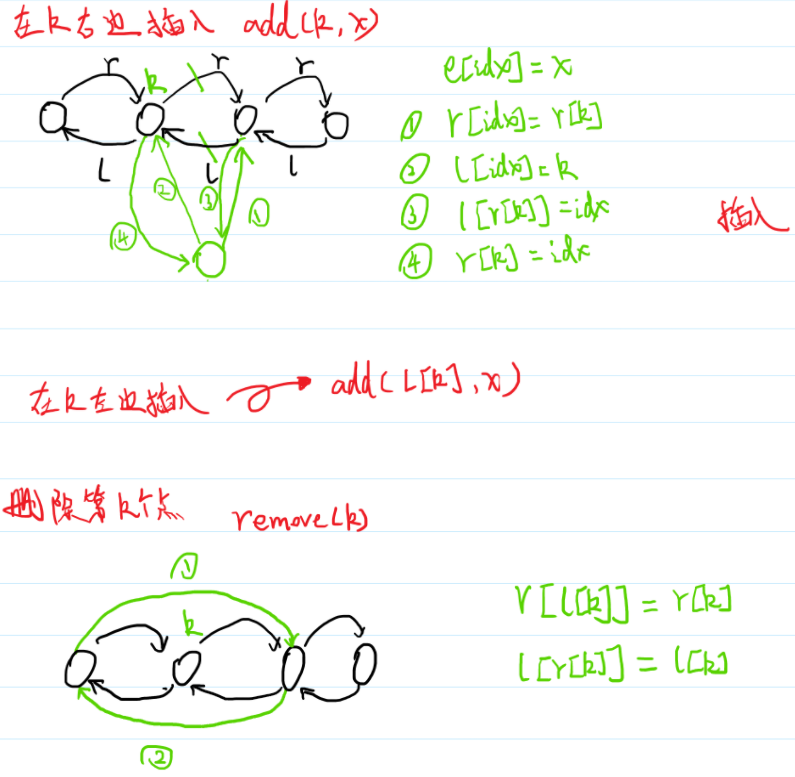
插入与删除操作：

注意插入、删除操作顺序不要搞错。

往左边插入一个点可以转化为往右边插入一个点，所以只要实现一次。

#include <iostream>
using namespace std;
const int N = 100010;
int e[N],l[N],r[N],idx;

void init(){// 链表初始化
    r[0] = 1,l[1] = 0;// 下标0和1分别表示最左、右边的哨兵
    idx = 2;// idx 此时已经用掉两个点0和1了
}       
// 将x插入下标是k的结点的右边
void add_to_right(int k,int x){
    e[idx] = x;
    r[idx] = r[k],l[idx] = k;
    l[r[k]] = idx,r[k] = idx;// 这两步顺序不能反
    idx ++;
}
// 删除下标为k的结点
void remove(int k){
    l[r[k]] = l[k],r[l[k]] = r[k];
}

int main(){
    ios::sync_with_stdio(false);

    int m;
    cin >> m;
    init();// 记得初始化
    
    string op;
    int x,y;
    while (m--){
        cin >> op;
        if (op == "L"){
            cin >> x;
            add_to_right(0,x);// 在最左端插入x等价于在0号哨兵右边插入x
        }
        if (op == "R"){
            cin >> x;
            add_to_right(l[1],x);// 在最右端插入x等价于在1号哨兵左边1个点的右边插入x
        }
        if (op == "D"){
            cin >> x;
            remove(x+1);// 删除第k个结点也就是删除下标为k+1的结点
        }
        if (op == "IL"){
            cin >> x >> y;
            add_to_right(l[x+1],y);// 在下标k+1的结点左侧插入等价于在它左边1个点的右侧插入
        }
        if (op == "IR"){
            cin >> x >> y;
            add_to_right(x+1,y);// 在下标k+1的结点右侧插入
        }
    }
	// 通过右指针遍历双链表
    for (int i = r[0];i != 1;i = r[i]) cout << e[i] << " ";
    return 0;
}

数组模拟栈。

例题：828. 模拟栈（模板题）

实现一个栈，栈初始为空，支持四种操作：
push x – 向栈顶插入一个数 x；
pop – 从栈顶弹出一个数；
empty – 判断栈是否为空；
query – 查询栈顶元素。
现在要对栈进行 M 个操作，其中的每个操作 3 和操作 4 都要输出相应的结果。

输入格式
第一行包含整数 M，表示操作次数。
接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式
对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。
其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示栈顶元素的值。

数据范围
1≤M≤100000,
1≤x≤10^9
所有操作保证合法。

输入样例：
10
push 5
query
push 6
pop
query
pop
empty
push 4
query
empty
输出样例：
5
5
YES
4
NO

数组模拟栈的操作非常简单。

#include <iostream>
using namespace std;
const int N = 100010;
int stk[N],top;// 栈数组stk以及栈顶指针初始化为0

int main(){
    ios::sync_with_stdio(false);

    int m;cin >> m;
    string op;
    int x;
    while (m--){
        cin >> op;
        if (op == "push"){
            cin >> x;
            stk[++top] = x;// 栈顶插入元素
        }
        if (op == "pop"){
            top--;// 栈顶弹出元素
        }
        if (op == "empty"){
            cout << (!top ? "YES" : "NO") << "\n";// 判断栈空
        }
        if (op == "query"){
            cout << stk[top] << "\n";// 输出栈顶元素
        }
    }
    return 0;
}