grant's Blog

记录生活中的点点滴滴

算法基础课笔记（八）

发表于 更新于 分类于 ，   阅读次数： Valine：
本文字数： 6.7k 阅读时长 ≈ 6 分钟

数组模拟队列。

例题：829. 模拟队列（模板题）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
实现一个队列，队列初始为空，支持四种操作：
push x – 向队尾插入一个数 x；
pop – 从队头弹出一个数；
empty – 判断队列是否为空；
query – 查询队头元素。
现在要对队列进行 M 个操作，其中的每个操作 3 和操作 4 都要输出相应的结果。

输入格式
第一行包含整数 M，表示操作次数。
接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式
对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。
其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示队头元素的值。

数据范围
1≤M≤100000,
1≤x≤10^9,
所有操作保证合法。

输入样例：
10
push 6
empty
query
pop
empty
push 3
push 4
pop
query
push 6
输出样例：
NO
6
YES
4

两种写法：（选择哪种看个人习惯，栈也是一样）

1.tt=-1, hh=0,q[++tt]=x, hh<=tt 表示队列非空

2.tt=0, hh=0,q[tt++]=x, hh<tt 表示队列非空

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
using  namespace std;
const int N = 100010;
int q[N],head = 0,tail = -1;// 队列数组q以及队头指针head=0与队尾指针tail=-1
// head > tail表示队列是空的
int main(){
    ios::sync_with_stdio(false);

    int n;cin >> n;

    string op;
    int x;
    while (n--){
        cin >> op;
        if (op == "push"){
            cin >> x;
            q[++tail] = x;// 队尾插入元素
        }
        if (op == "pop"){
            head ++;// 队头弹出元素
        }
        if (op == "empty"){
            cout << (head <= tail ? "NO" : "YES") << "\n";// 队列判空
        }
        if (op == "query"){
            cout << q[head] << "\n";// 输出队头元素
        }
    }
    
    return 0;
}

补充一个y总的循环队列的模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// hh 表示队头，tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;

// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;

// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh != tt){
}

2.2：单调栈与单调队列

什么是单调栈？

单调栈的定义：

  • 单调栈里面的元素具有单调性，单调递增或递减；
  • 元素加入栈前会把栈顶破坏单调性的元素删除，直到栈内元素满足单调性；

单调栈的用途如下：

  • 使用单调栈可以找到元素向左遍历的第一个比他小的元素（单增栈），也可以找到元素向左遍历第一个比他大的元素（单减栈）；单调栈的常见题型

  • 一般使用单调栈的题目具有以下的两点：

    ​ 离自己最近（栈的后进先出的性质）

    ​ 比自己大（小）、高(低)；

例题：830. 单调栈（模板题）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

输入格式
第一行包含整数 N，表示数列长度。
第二行包含 N 个整数，表示整数数列。

输出格式
共一行，包含 N 个整数，其中第 i 个数表示第 i 个数的左边第一个比它小的数，如果不存在则输出 −1。

数据范围
1≤N≤10^5
1≤数列中元素≤10^9
输入样例：
5
3 4 2 7 5
输出样例：
-1 3 -1 2 2

参考题解1： https://www.acwing.com/solution/content/13981/。

参考题解2： https://www.acwing.com/solution/content/27437/。（动图解释）

思路：

和双指针做法类似，先考虑一个暴力做法，再来想如何优化。

暴力做法很好写：

1
2
3
4
5
6
7
8
9
10
11
for (int i = 0;i < n;i++){
    int flag = 0;
    for (int j = i-1;j >= 0;j--){
        if (a[i] > a[j]){
            cout << a[j] << " ";
            flag = 1;
            break;
        }
    }
    if (flag == 0) cout << -1 << " ";
}

这肯定超时，时间复杂度为O(n^2)，需要优化。

现在求 a[t]左边第一个比它小的数， 考虑两个数，a[x] <= a[y] < a[t]，且x < y < t ，那么可能会输出a[y]，一定不会输出a[x]。

所以我们用到的数字序列必然是满足单调递增的，不满足单调性的数可以直接删掉，可以用单增栈来处理。

通过本题，单调栈的模型一共可用于4种题型，求序列中每个数左、右边第一个比它大、小的数。

图解：（来自上面参考题解1）

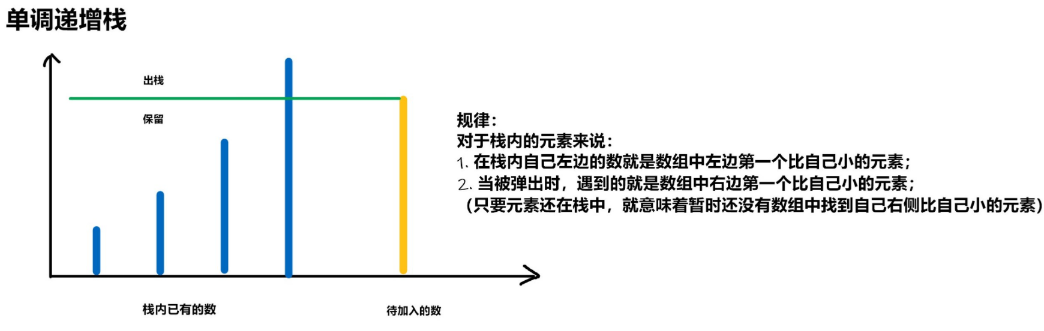
image-20211209224514405

对于将要入栈的元素来说，在对栈进行更新后（即弹出了所有比自己大的元素），此时栈顶元素就是数组中左侧第一个比自己小的元素；

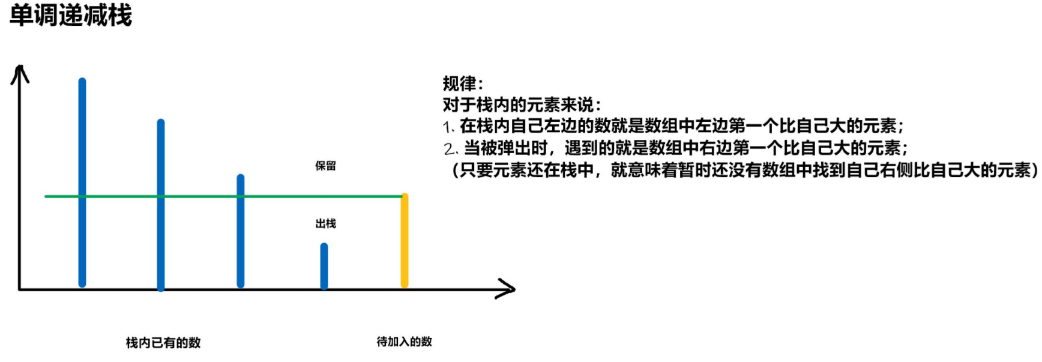
image-20211209224609514

对于将要入栈的元素来说，在对栈进行更新后（即弹出了所有比自己小的元素），此时栈顶元素就是数组中左侧第一个比自己大的元素。

y总代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
using namespace std;
const int N = 1e5+5;
int stk[N],top;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);// 加速cin、cout
    int n;cin >> n;
    
    int x;
    for (int i = 0;i < n;i++){
        cin >> x;
        while (top && stk[top] >= x) top--;// 栈顶元素>=当前待入栈元素且栈非空，则出栈
        // 当stk[top] == x时，新来的元素肯定离右边的元素更近，只能保留新的元素
        if (top) cout << stk[top] << ' ';// 若栈非空，栈顶元素就是左侧第一个比它小的元素
        else cout << -1 << ' ';// 栈空说明找不到，输出-1
        stk[++top] = x;// 将x入栈
    }
    return 0;
}

时间复杂度分析：对于序列中每个数，最多进栈一次加出栈一次，所以是O(n)。

关于cin加速的补充：cin.tie(NULL);// NULL可以换成0，cout也是类似的。

在ACM里，经常出现数据集超大造成 cin TLE的情况。在默认的情况下cin绑定的是cout，每次执行 << 操作符的时候都要调用flush，这样会增加IO负担。可以通过tie(0)（0表示NULL）来解除cin与cou t的绑定，进一步加快执行效率。

ios::sync_with_stdio(false);的优化效果比起上面的要差不少。

scanf\printf速度比较快，而且很少出问题。cin\cout的优化可能会导致一些bug，不要混用scanf。

什么是单调队列？

单调队列：可以用来维护（给定大小的）区间的最值，其时间复杂度为O(n)，其中n为序列的元素个数。

  • 单调递增队列：保证队列头元素一定是当前队列的最小值，用于维护区间的最小值。
  • 单调递减队列：保证队列头元素一定是当前队列的最大值，用于维护区间的最大值。

参考秦大佬讲义： https://www.acwing.com/blog/content/150/。

参考资料： https://www.jianshu.com/p/e59d51e1eef5。

滑动窗口是单调队列的最典型应用。单调队列还能用于多重背包的优化。

例题：154. 滑动窗口（模板题）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
给定一个大小为 n≤10^6 的数组。
有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。
你只能在窗口中看到 k 个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子：
该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。

窗口位置	        最小值	最大值
[1 3 -1] -3 5 3 6 7	 -1	    3
1 [3 -1 -3] 5 3 6 7	 -3	    3
1 3 [-1 -3 5] 3 6 7	 -3	    5
1 3 -1 [-3 5 3] 6 7	 -3	    5
1 3 -1 -3 [5 3 6] 7	  3	    6
1 3 -1 -3 5 [3 6 7]	  3	    7
你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式
输入包含两行。
第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。
第二行有 n 个整数，代表数组的具体数值。
同行数据之间用空格隔开。

输出格式
输出包含两个。
第一行输出，从左至右，每个位置滑动窗口中的最小值。
第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：
8 3
1 3 -1 -3 5 3 6 7
输出样例：
-1 -3 -3 -3 3 3
3 3 5 5 6 7

本题可以用单调队列、线段树、ST表等算法解决。

单调队列算法思路与单调栈类似，先考虑一个暴力做法，再来想如何优化，删除不满足单调性元素。

暴力做法很好写：

用队列来模拟滑动窗口，直接遍历窗口中所有元素取极值。

时间复杂度是O(n*k)，k是窗口大小，窗口滑动次数是O(n)级别。

先来看如何求最小值。

我们可以发现一个性质：

如果队列中存在两个元素，满足 a[i] >= a[j] 且 i < j，那么无论在什么时候我们都不会取 a[i] 作为最小值了，所以可以直接将 a[i] 删掉；

此时队列中剩下的元素严格单调递增，所以队头就是整个队列中的最小值，可以用 O(1)的时间找到；

为了维护队列的这个性质，我们在往队尾插入元素之前，先将队尾>=当前数的元素全部弹出即可；
这样所有数均只进队一次，出队一次，所以时间复杂度是 O(n) 的。

图解：

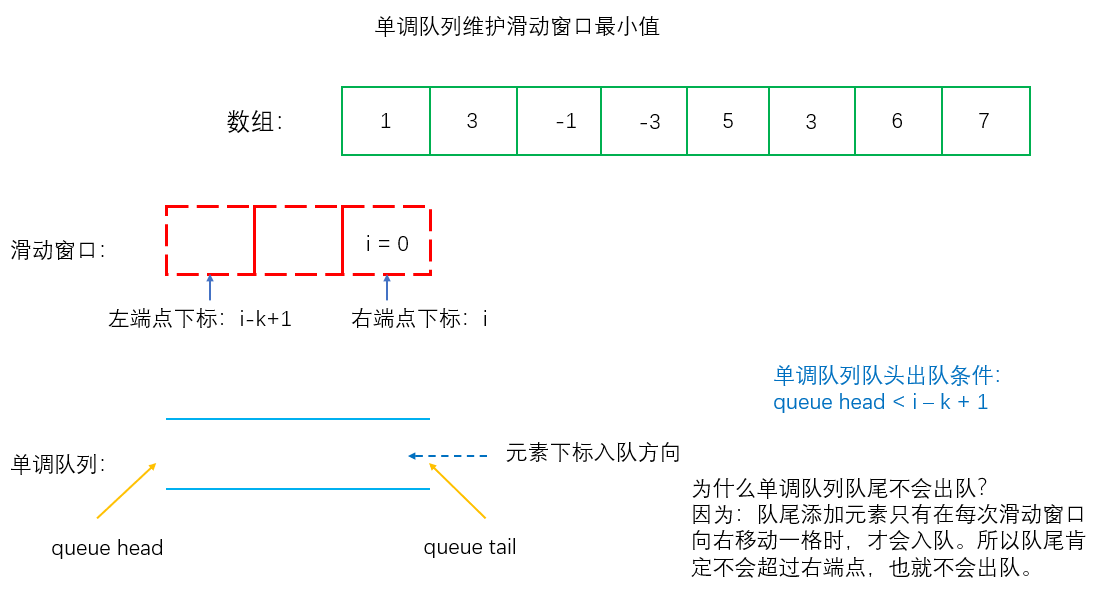
image-20211005231245493

有了单调的性质，单调队列不仅能很快求出最值，也能结合二分找到特定值。

1.y总手写单调队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
using namespace std;
const int N = 1e6+5;
int a[N],q[N];

int main(){
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);

    int n,k;
    cin >> n >> k;
    for (int i = 0;i < n;i++) cin >> a[i];

    // 求滑动窗口最小值，最大值类似
    // 注意：队列中存的是数组下标
    int head = 0,tail = -1;
    for (int i = 0;i < n;i++){
        // 注意i和队列起点q[head]一致
        // 队列非空，判断队头是否已经滑出窗口，由于for循环每次滑动1格，用if就行
        if (head <= tail && i-k+1 > q[head]) head++;// 这里把if改成while一样可以
        // 一般情况可以写成while不会出错
        // 等价于k < 当前滑动窗口的大小：i - q[head] + 1
        // 队列非空，若队尾元素不满足单调性则出队
        while (head <= tail && a[q[tail]] >= a[i]) tail--;
        // 将当前元素的数组下标从队尾入队
        q[++tail] = i;// 注意：必须先将当前元素下标入队再输出，有可能刚入队的就是答案
        // 特判，只有窗口完全装满才输出结果，窗口左端点i-k+1从0开始才输出
        if (i >= k-1) cout << a[q[head]] << ' ';
    }
    cout << "\n";
    // 求滑动窗口最大值
    head = 0,tail = -1;// 重置队列
    for (int i = 0;i < n;i++){
        if (head <= tail && i-k+1 > q[head]) head++;
        while (head <= tail && a[q[tail]] <= a[i]) tail--;// 将>=改成<=就行
        q[++tail] = i;
        if (i >= k-1) cout << a[q[head]] << ' ';
    }
    return 0;
}

时间复杂度：每个元素只会入队一次, 出队一次, 因此时间复杂度为O(n)。

单调队列是一种特殊的队列，可以从队头、队尾弹出元素，队尾插入元素，就是双端队列的一种。

关于队头是否滑出窗口的解释：

i - k + 1是以i为右端点、长度为k的区间的左端点，如果q[head]的值比左端点小，那就说明队头节点已经不在区间中了，需要弹出。

为什么队列中存的是数组下标而不是元素值？

存放元素值也能做但比较复杂。判断队头元素是否还在窗口中，这一步需要用到下标，存下标比较方便。数组下标唯一，而元素值不一定唯一。

2.STL deque双端队列。（比手写要慢约1倍）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <deque>
using namespace std;

const int N = 1e6+5;
int a[N];
deque<int> q;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    int n,k;
    cin >> n >> k;

    for (int i = 0;i < n;i++) cin >> a[i];
	// 也可以开2个deque放在一个for循环同时处理
    for (int i = 0;i < n;i++){
        while (!q.empty() && i-k+1 > q.front()) q.pop_front();
        while (!q.empty() && a[q.back()] >= a[i]) q.pop_back();
        q.push_back(i);
        if (i-k+1 >= 0) cout << a[q.front()] << ' ';
    }
    cout << "\n";
    q.clear();// 重置队列
    for (int i = 0;i < n;i++){
        while (!q.empty() && i-k+1 > q.front()) q.pop_front();
        while (!q.empty() && a[q.back()] <= a[i]) q.pop_back();
        q.push_back(i);
        if (i-k+1 >= 0) cout << a[q.front()] << ' ';
    }
    return 0;
}

注意：单调栈与单调队列在插入、弹出元素时要保证栈、队内元素的严格单调性，判断时必须取等号。

如果不是严格单调则不必加上等号。

坚持原创技术分享，您的支持将鼓励我继续创作！