算法提高课笔记（五）

272. 最长公共上升子序列

熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。
小沐沐先让奶牛研究了最长上升子序列，再让他们研究了最长公共子序列，现在又让他们研究最长公共上升子序列了。
小沐沐说，对于两个数列 A 和 B，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。
奶牛半懂不懂，小沐沐要你来告诉奶牛什么是最长公共上升子序列。
不过，只要告诉奶牛它的长度就可以了。
数列 A 和 B 的长度均不超过 3000。

输入格式
第一行包含一个整数 N，表示数列 A，B 的长度。
第二行包含 N 个整数，表示数列 A。
第三行包含 N 个整数，表示数列 B。

输出格式
输出一个整数，表示最长公共上升子序列的长度。

数据范围
1≤N≤3000,序列中的数字均不超过 2^31 − 1。

输入样例：
4
2 2 1 3
2 1 2 3
输出样例：
2

前置知识：

最长公共子序列：算法基础课笔记（二五）

最长上升子序列：算法基础课笔记（二四）

最长公共上升子序列：

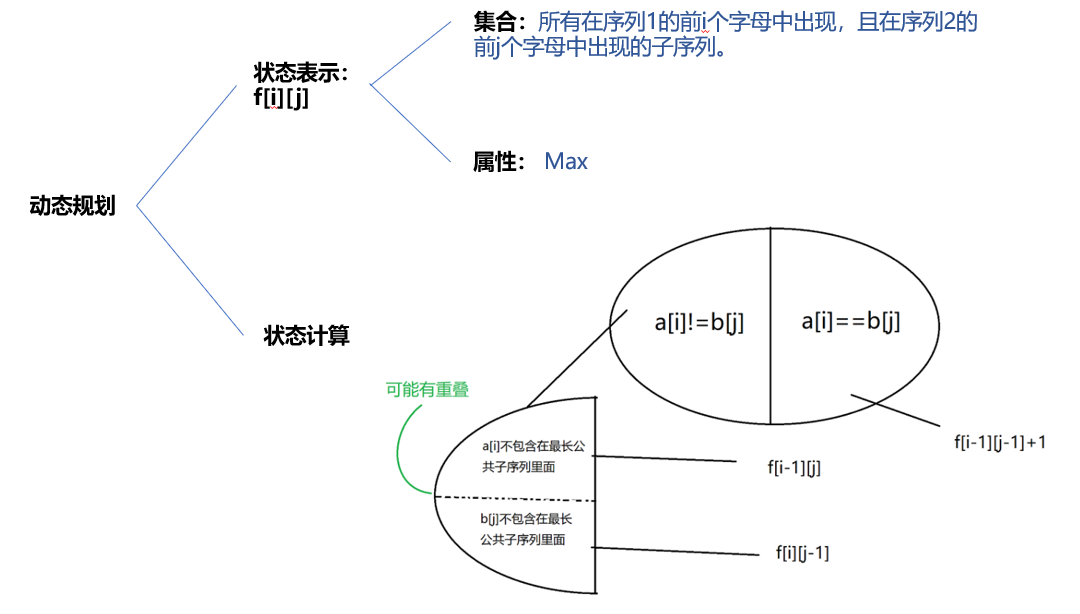
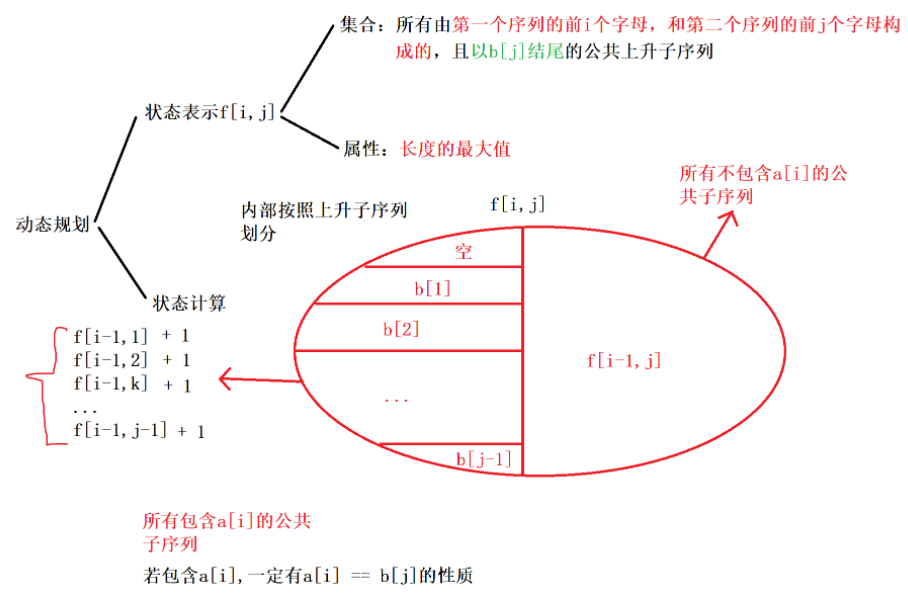
状态表示如上图所示，下面分析一下f[i][j]的状态计算。（可以参考蓝书）

以b[j]结尾，那么f[i][j]表示的公共上升子序列就一定有b[j]。

当a[i] != b[j]时，也就是所有不包含a[i]的公共上升子序列（因为b[j]是这些序列的结尾，要求公共而a[i] != b[j]），只需要考虑 a数组的 1~i-1这一段，所以f[i][j] = f[i-1][j]；
当a[i] == b[j]时，也就是所有以a[i]/b[i]结尾的公共上升子序列。也许你会相当然认为f[i][j] = f[i-1][j-1] + 1，这样想就错了；此时所有公共上升子序列都有共同的结尾，我们考虑它们的倒数第二个位置是谁，前面的想法已经固定了这个位置是b[j-1]，这是错的，按照LIS问题，这个位置可以取{空，b[1],b[2],...,b[j-1]}，所以f[i][j] = max {f[i-1][k] + 1, 0 <= k < j, b[k] < b[j] }，要考虑b[j]的前一个位置必须比它小才能计算。

题解一：三重循环二维朴素做法。时间复杂度：O(n^3)，TLE。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3005;
int a[N],b[N],f[N][N];
int n;

int main(){
    cin >> n;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= n; i ++ ) cin >> b[i];
    
    int ans = 0;
    for (int i = 1;i <= n;i ++){
        for (int j = 1;j <= n;j ++){
            f[i][j] = f[i-1][j]; // 一般情况，a[i] != b[j]
            if (a[i] == b[j]){
                f[i][j] = max(f[i][j],1); // 倒数第二个位置为空，LCIS长度为1
                for (int k = 1;k < j;k ++){
                    if (b[k] < b[j])
                        f[i][j] = max(f[i][j],f[i-1][k] + 1);
                }
            }
            ans = max(ans,f[i][j]);
        }
    }
    
    cout << ans << '\n';
    return 0;
}

题解二：二重循环二维DP优化做法。时间复杂度：O(n^2)。

再次强调，99%的DP优化就是对朴素代码做等价变形。

观察到朴素做法中f[i][j] = max(f[i][j],f[i-1][k] + 1);这里每次更新第i个状态用到的都是第i-1个状态，所以可以用一个变量maxv来存储上一阶段可以放在b[i]之前的最大的状态值。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3005;
int a[N],b[N],f[N][N];
int n;
int main(){
    cin >> n;
    
    for (int i = 1;i <= n;i ++) cin >> a[i];
    for (int i = 1;i <= n;i ++) cin >> b[i];
    
    int ans = 0;
    for (int i = 1;i <= n;i ++){
        int maxv = 1;// maxv 表示 max{f[i-1][k] + 1, 0 <= k < j, b[k] < b[j]}
        for (int j = 1;j <= n;j ++){
            f[i][j] = f[i-1][j];
            // 对于a[i] == b[j]的情况做等价变形
            if (a[i] == b[j]) f[i][j] = max(f[i][j],maxv);
            if (b[j] < a[i]) maxv = max(maxv,f[i-1][j] + 1);
            
            ans = max(ans,f[i][j]);
        }
    }
    cout << ans << '\n';
    return 0;
}

题解三：二重循环一维DP优化做法。时间复杂度：O(n^2)。

参考题解： https://www.acwing.com/solution/content/11227/。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3005;
int a[N],b[N],f[N];
int n;
int main(){
    cin >> n;
    
    for (int i = 1;i <= n;i ++) cin >> a[i];
    for (int i = 1;i <= n;i ++) cin >> b[i];
    
    int ans = 0;
    for (int i = 1;i <= n;i ++){
        int maxv = 1;// maxv 表示 max{f[i-1][k] + 1, 0 <= k < j, b[k] < b[j]}
        for (int j = 1;j <= n;j ++){
            // 对于a[i] == b[j]的情况做等价变形
            if (a[i] == b[j]) f[j] = max(f[j],maxv);
            if (b[j] < a[i]) maxv = max(maxv,f[j] + 1);
            
            ans = max(ans,f[j]);
        }
    }
    cout << ans << '\n';
    return 0;
}