考研算法辅导课笔记（九）

真题讲解

2012-6

答案：C

分析：邻接矩阵主对角线以下元素均为0说明不存在i-->j && i < j的边，所以拓扑序列存在且可能不唯一。（说明：408数据结构中的图只考虑简单图，所以不用考虑自环和重边）

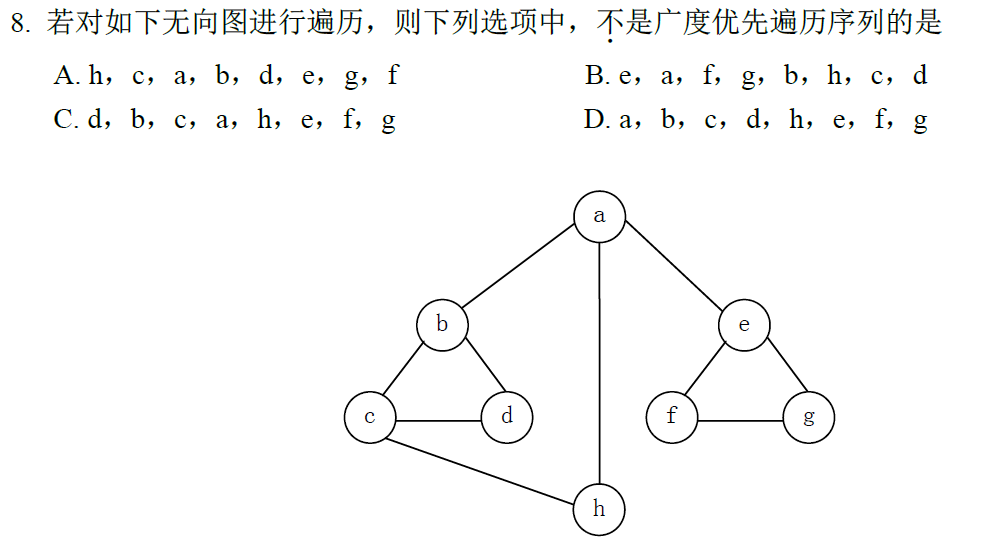
2013-8

广度优先遍历，就是距离从小到大的遍历顺序。

如果担心直接看看不准，可以把各点到起点的距离求出来，看看是不是从小到大的顺序。

答案选D。

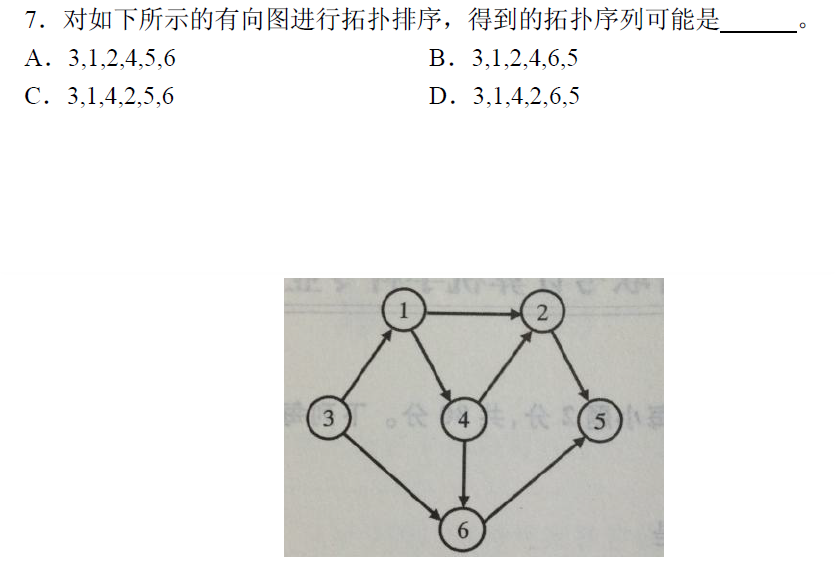
2014-7

拓扑序列求解流程：

1. 找到所有入度为0的节点入队；
2. 将入度为0的节点出队，然后将其所指向的所有边删掉；
3. 重复1,2步骤，直到所有节点都已经入队、出队，则存在拓扑序列，否则不存在。

答案选D。

2015-5

画图，手动枚举。

答案选D。

2017-7

在无向图中，每条边将贡献两个度。所以16条边将贡献32个度。

答案选B。题目中已给出24个度，还缺8个度，剩余节点每个最多贡献2个度，所以至少要11个顶点。

个人做法，画图，把给出的点都摆出来，像拼积木一样，非常麻烦，不建议使用（除非时间多用来验证理论答案），记住结论就行。

---

从以上题目大概可以总结出一些规律，答案大概率是后两个选项，所以可以从后往前看。

第八讲 最小生成树、最短路、关键路径

1. 最小生成树
   (1) Prim
   (2) Kruskal
2. 最短路
   (1) 单源最短路 Dijkstra
   (2) 多源汇最短路 Floyd
3. 关键路径

---

我们定义无向连通图的 最小生成树（Minimum Spanning Tree，MST）为边权和最小的生成树。

注意：只有连通图才有生成树，而对于非连通图，只存在生成森林。

给定一个无向图，在图中选择若干条边把图的所有节点连起来，要求边长之和最小。在图论中，叫做求最小生成树。（一般只考虑无向图的最小生成树，拓展：有向图的最小生成树称之为最小树形图，通过朱刘算法解决）

只作为了解：MST还有一种定义方式，就是最大边权最小，两种定义方式本质上相同。

MST的知识点可以参考算法基础课笔记（十一）。

MST的相关结论：

• 删去MST的一条边，它将变成非连通图；给MST加上一条边，它将形成回路。

• MST不一定是唯一的，当无向连通图中所有边权值都不相同时MST唯一确定（充分不必要条件）。

• 若无向连通图本身是一棵树，那么它自己就是MST。

• 对于n个顶点的无向连通图来说，如果最小生成树存在，那么它的边数一定是n-1。

次小生成树：拓展内容！

将MST中的所有边称为树边，不在MST中的其余无向连通图中的边称为非树边。

先建出一棵最小生成树，满足使用的边都是最小的，剩下的边（称为非树边）一定没有树边优。如果我们加入一条非树边，删除最小生成树中的权值最大边，次小生成树一定是包括在以这种方法建出的树中的。

如果次小生成树也是一棵MST，就说明MST不唯一。

---

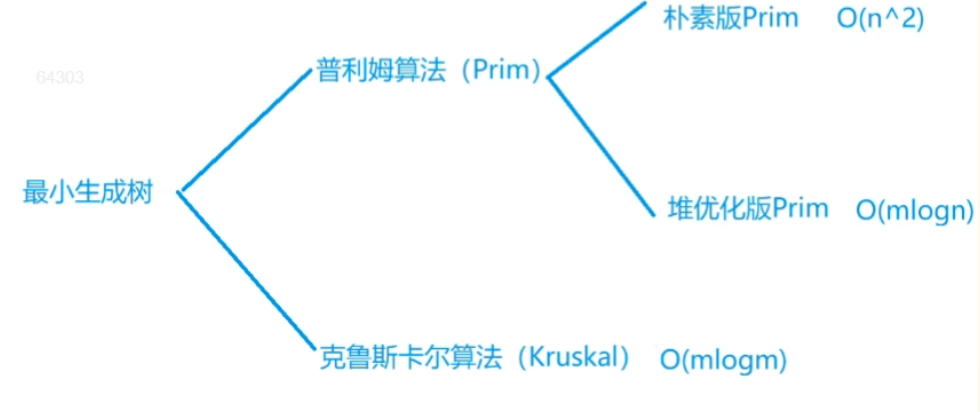
求解MST的三种算法。

对于最小生成树，稠密图常用朴素版Prim算法，稀疏图常用Kruskal算法，堆优化Prim用的较少。

最小生成树的两种算法都能处理负权和负环。最小生成树中不应该有自环。

Kruskal算法的时间复杂度也可以说是O(mlogn)，因为一般有m < n^2，所以O(mlogm)~O(mlogn)。

Prim算法（代码必掌握！）

Prim算法和Dijkstra算法非常像，同样基于贪心思想。Prim可以处理带负权图。

该算法的基本思想是从一个结点开始，不断加点（而不是 Kruskal 算法的加边）。

y总算法基础课讲解视频： https://www.acwing.com/video/25/ 12:13。（很细致）

acwing.858. Prim算法求最小生成树

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。
求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E)，其中 V 表示图中点的集合，E 表示图中边的集合，n=|V|，m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。

输入格式
第一行包含两个整数 n 和 m。
接下来 m 行，每行包含三个整数 u,v,w，表示点 u 和点 v 之间存在一条权值为 w 的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围
1≤n≤500,
1≤m≤10^5,
图中涉及边的边权的绝对值均不超过 10000。

输入样例：
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例：
6

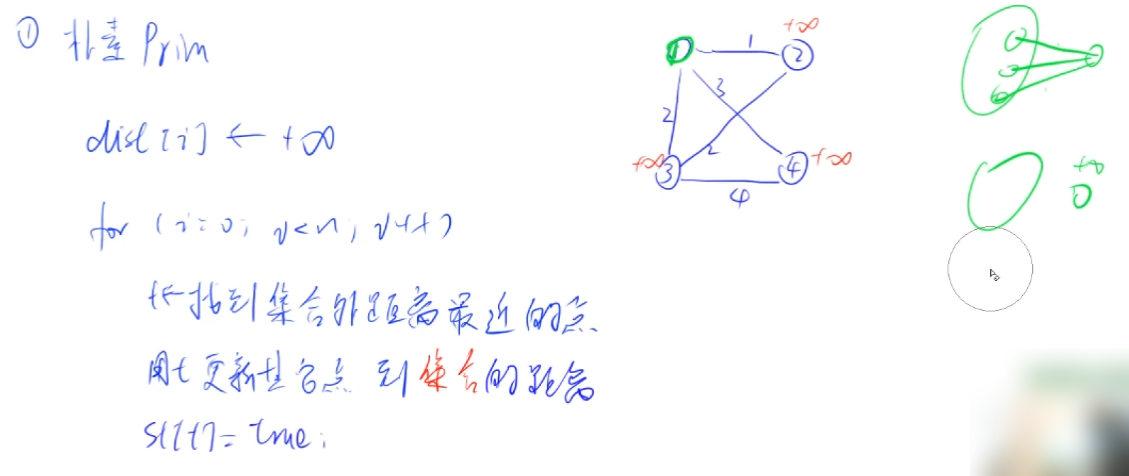
图解prim算法求解MST。

还可以参考算法基础课笔记（二一）的题解。

prim算法：每次将离连通部分的最近的点和点对应的边加入的连通部分，连通部分逐渐扩大，最后将整个图连通起来，并且边长之和最小。

prim算法伪代码流程：

定义点到集合的距离：当集合外一点有多条边连向集合内的点，取权值最小的边作为点到集合的距离。

若集合外一点没有边连向集合内的点，则定义点到集合的距离为INF。

这里的集合也就是最小生成树的连通块，迭代n次，每次迭代将一个点将入到集合中。

dist数组存的是点到集合的距离，和Dijkstra不一样，Dijkstra是更新到起始点的距离。

时间复杂度：O(n^2)。

prim算法适合处理稠密图，用邻接矩阵存储。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 505,M = 1e5+5,INF = 0x3f3f3f3f;
int n,m;
int di[N],g[N][N];
bool st[N];

int prim(){
    memset(di,0x3f,sizeof di); // 各点到集合距离初始化为INF
    
    di[1] = 0; // 第一个加入集合的点为1号，它到集合的距离初始化为0
    int res = 0; // 计算MST的边权之和
    for (int i = 0;i < n;i ++){ // n次循环，每次加入一个距离S最近的点t
        int t = -1;
        for (int j = 1;j <= n;j ++)
            if (!st[j] && (t == -1 || di[t] > di[j]))
                t = j;// 找到集合外离S最近的点t
        // 如果第2个及以后的点没有连向集合的边，MST不存在        
        if (di[t] == INF) return INF;
        st[t] = true;// t号点加入集合
        res += di[t]; // 先累加边权，再更新，否则可能会引入自环
        for (int j = 1;j <= n;j ++) // 用t更新各点到集合的距离
            di[j] = min(di[j],g[t][j]);
    }
    return res;
}

int main(){
    memset(g,0x3f,sizeof g);
    cin >> n >> m;
    
    int a,b,c;
    while (m--){
        cin >> a >> b >> c;
        // 本题注意处理重边
        // 考研时的图都是简单图，不需要考虑重边和自环
        // 取min时特别注意初始化为一个极大值
        g[a][b] = g[b][a] = min(g[a][b],c); // 如果有重边只取最小边
    }
    
    int t = prim();
    if (t == INF) cout << "impossible\n";
    else cout << t << '\n';
    return 0;
}

图论这块代码要掌握好，代码中的细节是最全面的，文字流程可能遗漏细节。

Kruskal 算法

Kruskal 算法是一种常见并且好写的最小生成树算法，由 Kruskal 发明。该算法的基本思想是从小到大加入边，是个贪心算法。

Prim采用点贪心，Kruskal采用边贪心。

前置知识：并查集，图的存储。

Kruskal 算法的时间瓶颈就是第一步的边权排序O(m*logm)。（快排的常数比较小）

acwing.859. Kruskal算法求最小生成树

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。
求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E)，其中 V 表示图中点的集合，E 表示图中边的集合，n=|V|，m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。

输入格式
第一行包含两个整数 n 和 m。
接下来 m 行，每行包含三个整数 u,v,w，表示点 u 和点 v 之间存在一条权值为 w 的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围
1≤n≤10^5,
1≤m≤2∗10^5,
图中涉及边的边权的绝对值均不超过 1000。

输入样例：
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例：
6

时间复杂度：O(mlogm)。

kruskal算法适合处理稀疏图，用三元组存储。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5+5,M = 2e5+5;
int p[N],n,m;

struct Edge{
  int a,b,c;
  
  bool operator< (const Edge& t) const{
      return c < t.c;
  }
}e[M];

int find(int x){
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main(){
    cin >> n >> m;
    
    for (int i = 1;i <= n;i ++) p[i] = i;
    
    int a,b,c;
    for (int i = 0;i < m;i ++){
        cin >> e[i].a >> e[i].b >> e[i].c;
    }
    
    sort(e,e+m); // 时间复杂度主要体现在这里，O(mlogm)
    
    int res = 0,cnt = 0;
    for (int i = 0;i < m;i ++){
        int a = e[i].a,b = e[i].b,c = e[i].c;
        int pa = find(a),pb = find(b);
        if (pa != pb){ // 如果a，b不连通，将它们所在集合合并，更新MST边权之和
            p[pa] = pb;
            res += c;
            cnt ++;
        }
        if (cnt == n-1) break; // n个点，MST共有n-1条边
    }
    
    if (cnt == n-1) cout << res << '\n';
    else cout << "impossible\n";
    return 0;
}