最短路
最短路一般分为单源最短路和多源汇最短路。
源点也就是起点,汇点也就是终点。
最短路问题的考察重点在于如何将问题抽象建图,而不在算法的正确性。(说白了多背模板)
最短路问题不考虑有向图和无向图的区别,因为无向图就是一种特殊的有向图。
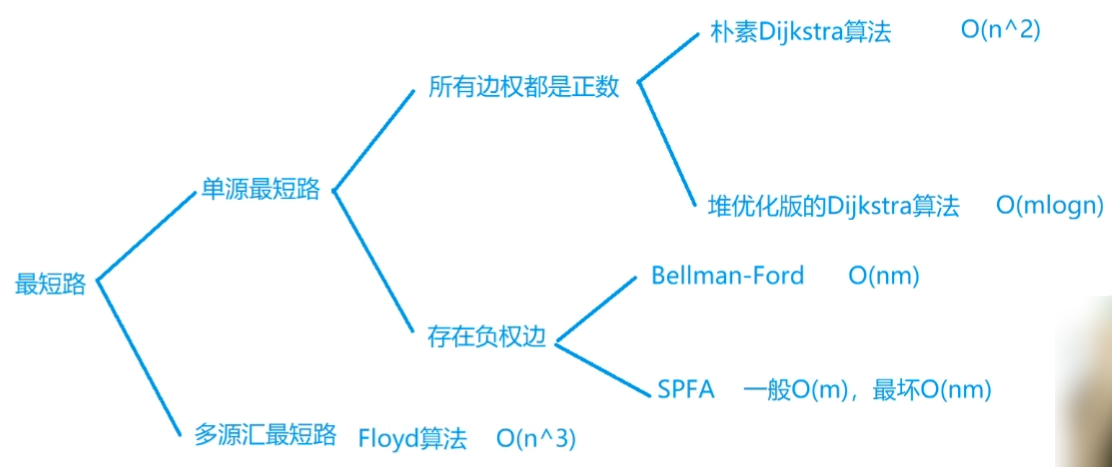
其中n表示点数,m表示边数。
稠密图(m~n^2同一级别)用朴素版的Dijkstra算法,稀疏图(m~n同一级别)用堆优化版的Dijkstra算法。
注:在考研408数据结构中,不考察单源最短路中的存在负权边的两种算法!
Dijkstra算法
它和prim算法很像,也分为朴素版和堆优化版两个版本。
用来求有权图的单源最短路径的算法,基于贪心思想。
这种算法只适用于非负权图,但是时间复杂度非常优秀。
acwing.849. Dijkstra求最短路 I
1 | 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。 |
题解参考算法基础课笔记(十八)。
一篇非常全面的题解。

存储方式:朴素版Dijkstra 算法适用于稠密图,而稠密图一般用邻接矩阵来存储。
时间复杂度:O(n^2+m)。
写法和prim算法非常相似。可以对比一下,两个算法的差别基本只有对dist[N]数组的更新方式的区别。
要注意的一点就是dijkstra输出的答案不需要累加,d[N]维护的就是起点到每个点的最短距离。
注意一下方向,这是有向图。
1 |
|
Floyd 算法
是用来求任意两个结点之间的最短路的,利用DP思想。
复杂度比较高,但是常数小,容易实现,也可以处理负权边。效率比执行 n次 Dijkstra 算法要好。
f[k,i,j]代表(k的取值范围是从1到n),在考虑了从1到k的节点作为中间经过的节点时,从i到j的所有路径的最小值。
形式化说明如下:
f[k][i][j]可以从两种情况转移而来:
【1】从f[k−1][i][j]转移而来,表示i到j的最短路径不经过k这个节点
【2】从f[k−1][i][k]+f[k−1][k][j]转移而来,表示i到j的最短路径经过k这个节点
那么f[k,i,j] = min(f[k-1,i,j], f[k-1,k,i] + f[k-1,k,j])。
因此在计算第k层的f[i,j]的时候必须先将第k - 1层的所有状态计算出来,所以需要把k放在最外层。
可以把k这一维度去掉,降低空间复杂度,f[i,j] = min(f[i,j], f[i,k] + f[k,j])。
acwing.854. Floyd求最短路
1 | 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。 |
题解参考算法基础课笔记(二十)。
一篇DP原理解析的题解。
1 |
|
Floyd和BF算法类似,会遍历所有的边,因此不管是不是和源点连通的边它都会得到更新,因此就算不存在x到y的最短路,距离INF会发生改变,但不至于超过一半,所以用INF/2来判断。
关键路径
简单示例参考博客;详细内容(废话)参考王道P234;代码实现与算法讲解参考算法笔记P417。
补充概念:
有向无环图简称为DAG图。用DAG图表示的工程网络称之为AOV网。
带权DAG图表示的工程网络称之为AOE网。AOE也就是一个拓扑图。
AOE网的边有权值,AOV网的边无权值。
关键路径是AOE网中的概念。
事件是点,活动是边!
在AOE网中,所有活动都完成才能到达终点,因此完成整个工程所必须花费的时间(即最短工期)应该为源点到终点的最大路径长度。具有最大路径长度的路径称为关键路径。关键路径上的活动称为关键活动。
关键路径并不唯一!
ETV(Earliest Time Of Vertex):事件最早发生时间,就是顶点的最早发生时间;
事件k的ETV指的是从源点到顶点k的最长路径长度。源点的ETV等于0。
LTV(Latest Time Of Vertex):事件最晚发生时间,就是每个顶点对应的事件最晚需要开始的时间;
事件k的LTV指的是汇点的LTV与从顶点k到汇点的最长路径长度之差。汇点的LTV等于汇点的ETV。
ETE(Earliest Time Of Edge):活动的最早开工时间,就是边的最早发生时间,就是边起点的最早发生时间;
LTE(Lastest Time of Edge):活动的最晚发生时间,就是边终点的最晚发生时间与该活动时间之差。
一句话总结:求出上述概念的结果的本质都是求最长路径长度!
拓扑图求最长路可以用DP来做。
真题讲解
2011-41

注意给出的是上三角,不包括对角线(408的图不考虑自环)。
答案:太简单,没什么好解释的。
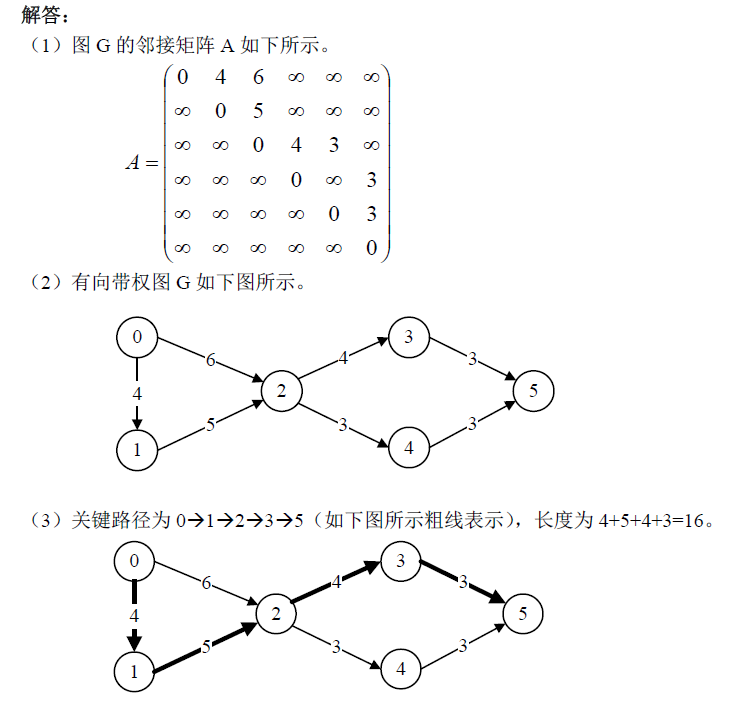
2012-7
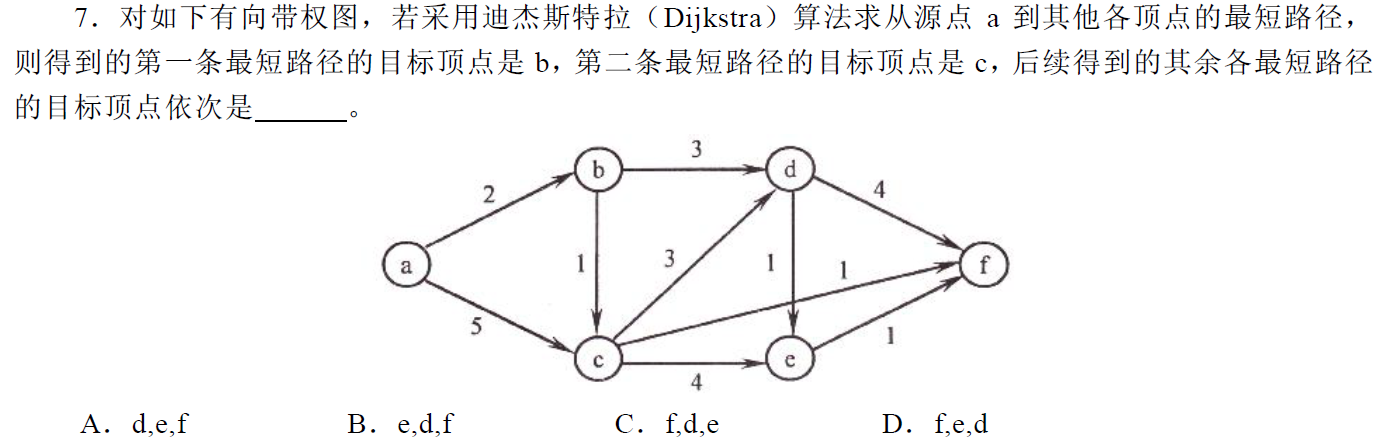
解答:
关键是掌握dijkstra算法的流程,每次将一个点加入st集合,找到离源点最近的点t,然后用t更新距离,将t加入st集合。所以依次求出最短路的点离源点的距离一定是递增的。
算出每个点到点a的最短距离,从小到大排序。
答案选C。
2012-8

1肯定是对的,最小生成树代价就是最小的,也就是唯一的。
2不一定,权值最小的边可能有多条。
3错,最小生成树不唯一。
4错。
答案选A。
2013-9
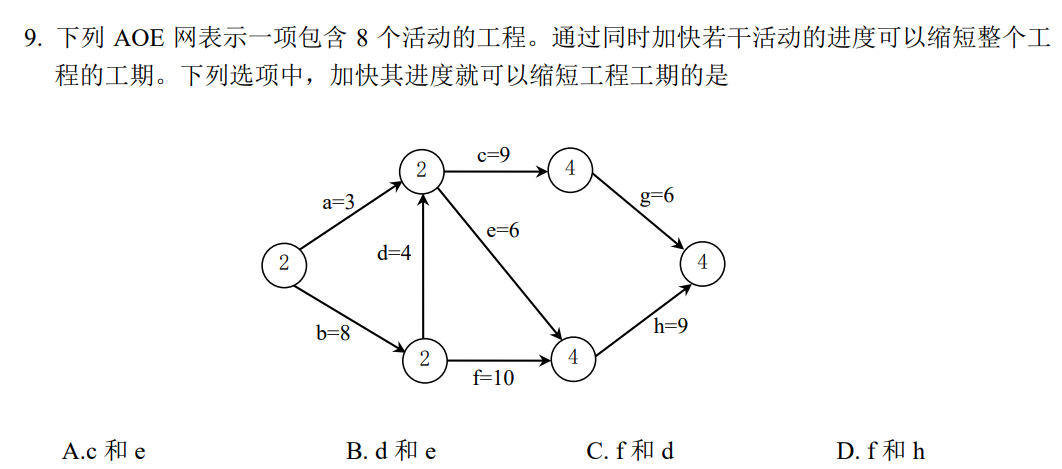
注意读题:将选项中的所有边进度同时加快,而不是分别加快哪条边的进度。
解法一:
先求出整个工程工期,然后分别将每个选项涉及到的边的权值降到0,看看对工程工期的影响。
答案选C。砍掉f和d可以缩短工期。
解法二:
求出全部关键路径为bfh, bdeh, bdcg。只有三条关键路径上的活动时间同时减少才能缩短工期。
答案选C。f和d包含在三条关键路径中。
2015-6
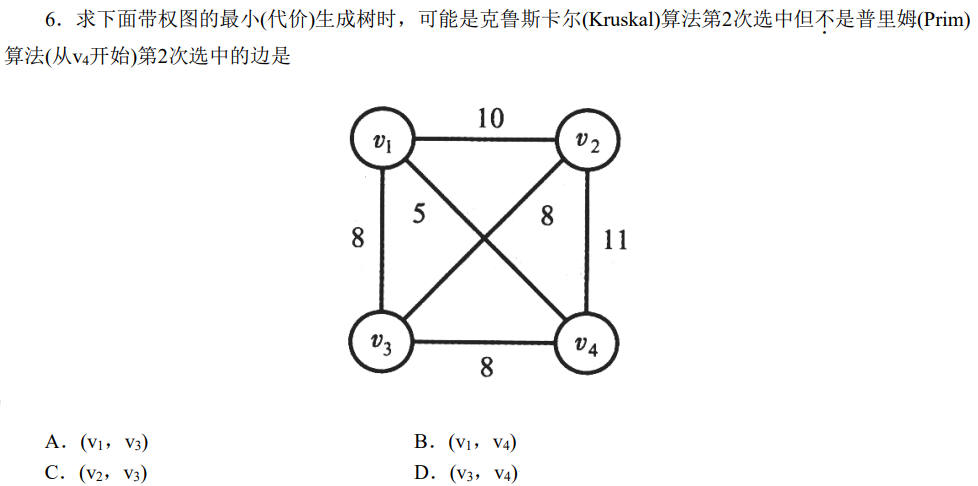
记住两种算法的核心思路:
Prim算法:点贪心,按集合外一点到集合的最小距离加点;
Kruskal算法:边贪心,按图中的最小边加边。
答案选C。
2015-42
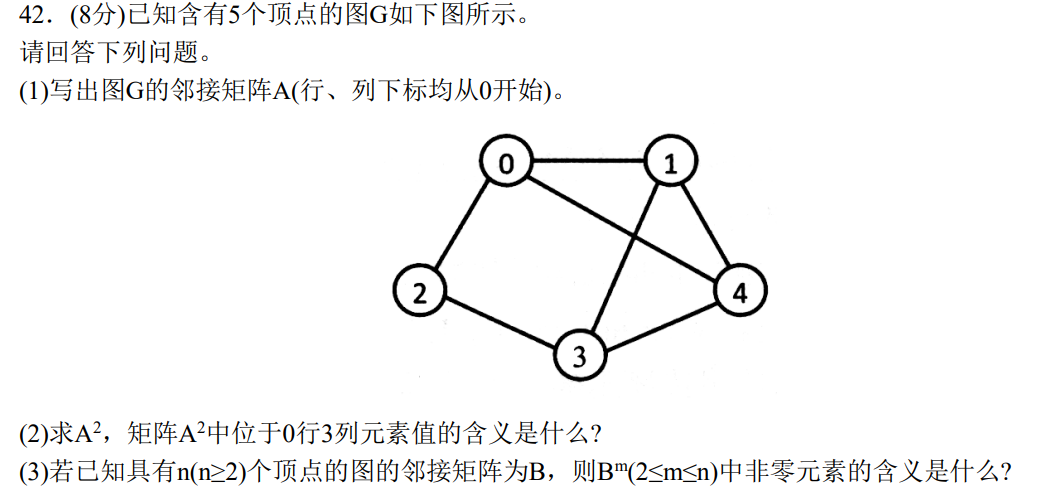
结论:设图G的邻接矩阵为A,则A^n[i][j]表示从i到j的长度为n的路径的数目。
运用DP的思维解释一下:
A^n[i][j]可以记为f[i,j,n],表示从i走到j长度为2的走法的数量。
为什么?
A^n[i][j] = sigma{A^(n-1)[i][k] * A[k][j]}, 0 <= k < n;
f[i,j,n] = sigma{f[i,k,n-1] * f[k,j,1]}, 0 <=k < n。
上面两个式子是等价的。
然后解释一下上面第二个DP转移式的意义:
从i走n步到j的方案可以通过从i走n-1步到k(0 <=k < n)然后从k走一步到j的方案转移而来。
根据最后一步的走法进行划分,最后一步可以由k(0 <=k < n)走到j。
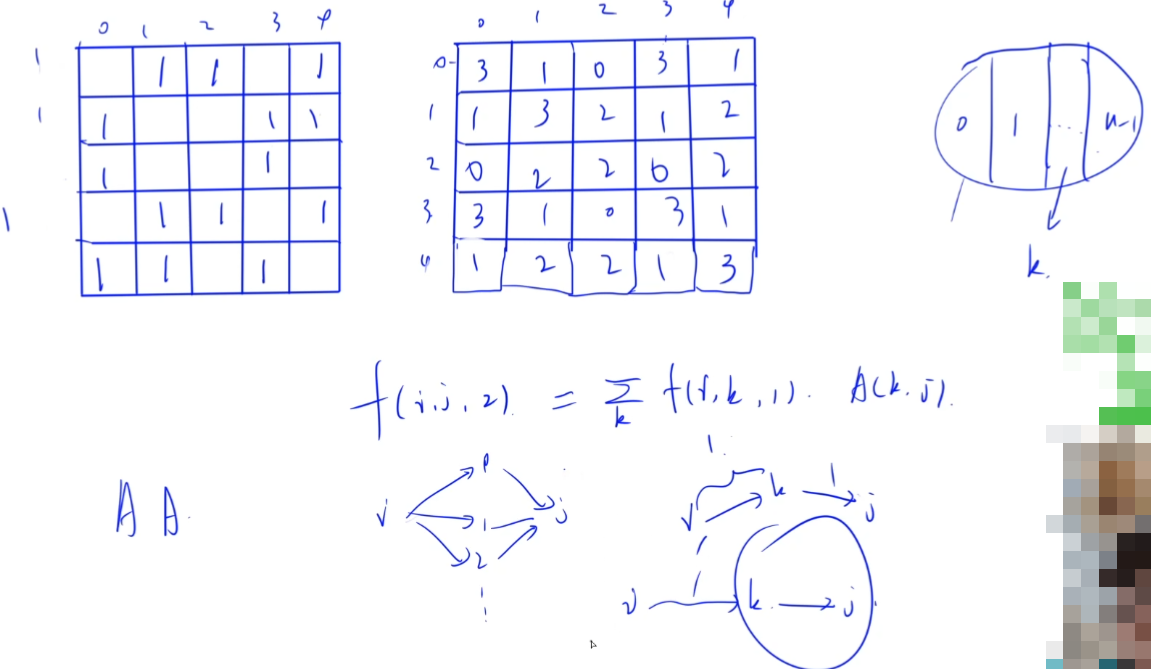
答案如下:

2016-8
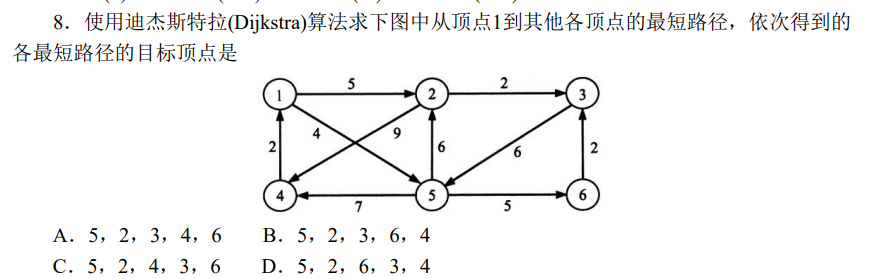
记住Dijkstra算法的核心思路:
它和Prim算法原理类似,都是点贪心,只不过区别是Dijkstra按源点到集合外一点的最小距离加点。
加点的顺序一定是按源点到各点最小距离递增排序的。
答案选B。
2017-42
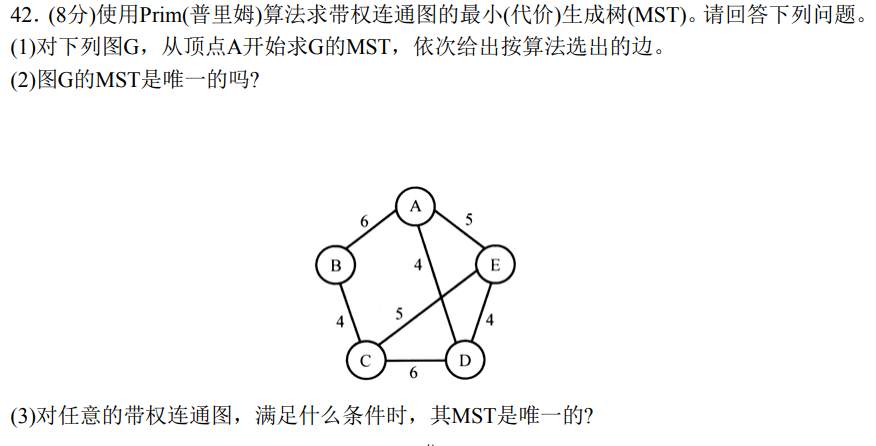
(1)Prim算法:点贪心,A->D->E->C->B。
(2)每次加点时都只有唯一的一条边,所以MST是唯一的。
(3)给出一个充分不必要条件即可,当图的任意两条边的权值都不等时MST是唯一的。
2018-42
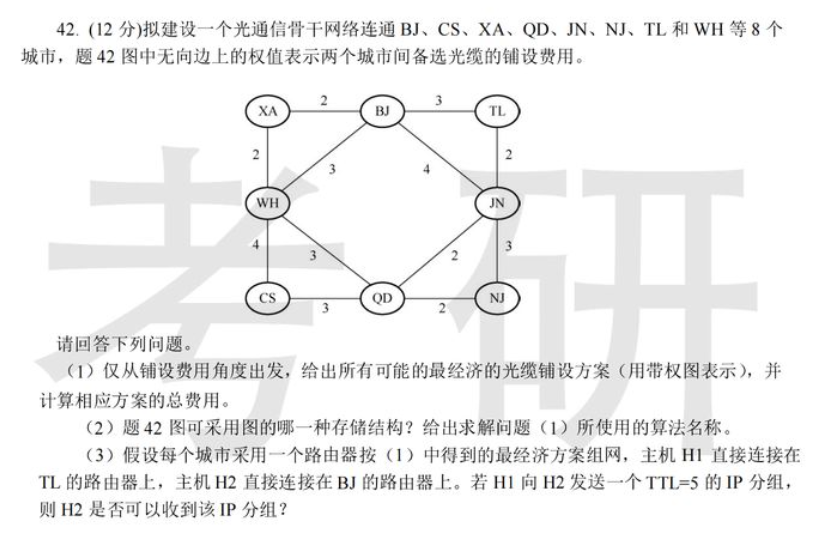
参考答案如下:
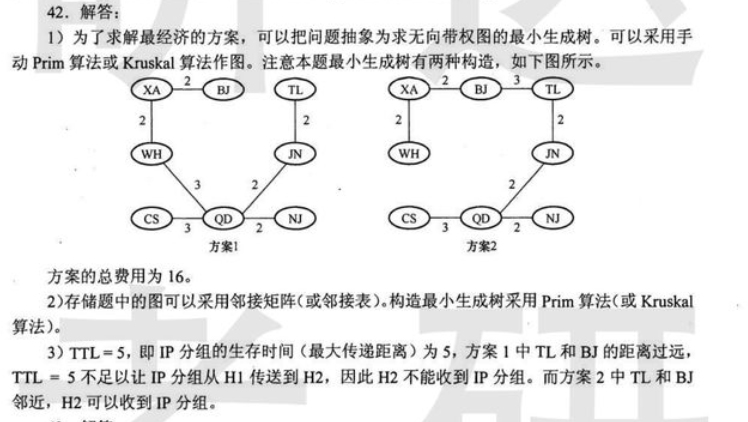
2019-5
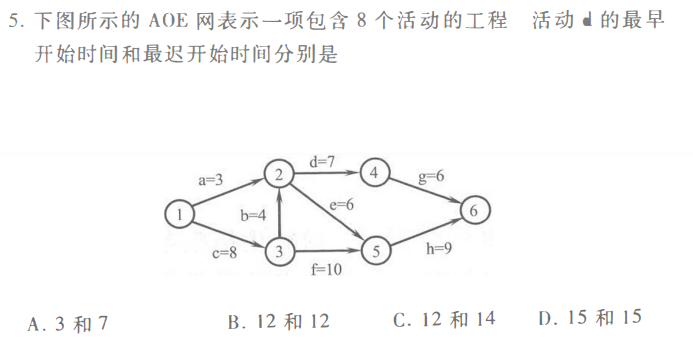
求事件、活动的最早、晚开始时间列表做法参考王道教材P235。
活动d的最早开始时间对应点2的最早开始时间,也就是1到2的最长路径长度,是12。
活动d的最晚开始时间就是点4的最晚开始时间减去d=7,也就是21-7 = 14。
答案选C。
2020-8

答案选B,基础概念。

