算法基础课笔记（十五）

三：搜索与图论

第三章：搜索与图论模板整理， https://www.acwing.com/blog/content/405/

3.1：DFS

在蓝桥杯（一）、（二）介绍过递归（DFS）。

DFS与BFS对比：

搜索	数据结构	空间复杂度
DFS	stack	O(h),h为层数
BFS	queue	O(2^h),h为层数，二叉树每层约2^(h-1)节点

还有一个重要区别：DFS不具有最短路性质，而BFS具有最短路性质，可以搜到最短路径。

对空间要求比较高的一般用DFS，需要用到最短路的用BFS。

例题1：842. 排列数字（模板题）

一道在蓝桥杯中类似的题目。

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。
现在，请你按照字典序将所有的排列方法输出。

输入格式
共一行，包含一个整数 n。

输出格式
按字典序输出所有排列方案，每个方案占一行。

数据范围
1≤n≤7
输入样例：
3
输出样例：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

#include <iostream>
using namespace std;
#define IOS \
    ios::sync_with_stdio(false); \
    cin.tie(0); \
    cout.tie(0)
const int N = 10;
int st[N];// 存放递归树每一层选择的数字
bool used[N];// 判重，看数字i是否被用过
int n;

void dfs(int u){
    if (u > n){// 递归边界
        for (int i = 1;i <= n;i ++) cout << st[i] << ' ';
        cout << '\n';
        return;
    }
    
    for (int i = 1;i <= n;i ++){
        if (!used[i]){// 数字i没有被用过，才可以选择
            st[u] = i;// 选择数字i
            used[i] = true;// 记录数字i被用过
            dfs(u + 1);// 递归下一层
            
            st[u] = 0;// 恢复现场
            used[i] = false;
        }
    }
}

int main(){
    IOS;
    
    cin >> n;
    dfs(1);
    return 0;
}

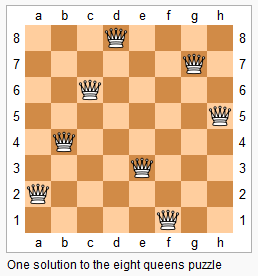
例题2：843. n-皇后问题（模板题）

n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。
现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式
共一行，包含整数 n。

输出格式
每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后，输出一个空行。
注意：行末不能有多余空格。
输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围
1≤n≤9
输入样例：
4
输出样例：
.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

n-皇后问题也是一个经典的DFS问题。

参考题解： https://www.acwing.com/solution/content/2820/。

算法1：DFS按每行枚举。递归实现排列型枚举。

通过题目知道，每行每列必须放1个皇后，这样才能保证不会被攻击。

和数字全排列一样，只需要枚举列数的全排列就行，然后再判断对角线、反对角线上是否只有1个皇后，若斜线上存在冲突则剪枝处理。

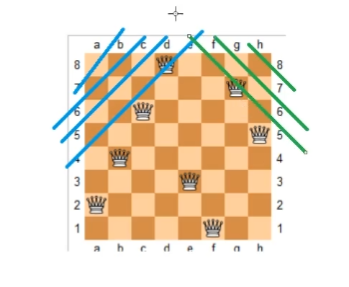
蓝色线表示第1,2,3条反对角线，绿色线表示第1,2,3条对角线。

dfs的时候，u表示行数，i表示列数，都从0开始！

棋盘上所有点都映射为坐标：(u,i)，范围(0,0)到(n-1,n-1)。

我们利用直线的截距来唯一确定这条直线上所有棋盘坐标都在同一对角、反对角线上。

对角线dg[u+i]表示直线i=-u+b，截距b=u+i，一定是正数；

反对角线udg[n-u+i]表示直线i=u+b，截距b=i-u，可能为负数，所以加上一个偏移量n使结果为正，

取i-u+n，偏移量任取，只要使得其为正数就行。

#include <iostream>
using namespace std;
#define IOS \
    ios::sync_with_stdio(false); \
    cin.tie(0); \
    cout.tie(0)
const int N = 20;// 对角线数量是2*n-1
bool used[N],dg[N],udg[N];// 判断某列，对角线，反对角线是否用过
char g[N][N];
int n;

void dfs(int u){
    if (u == n){// 递归边界
        for (int i = 0;i < n;i ++){
            for (int j = 0;j < n;j ++) cout << g[i][j];
            cout << '\n';
        }
        cout << '\n';
        return;
    }
    
    for (int i = 0;i < n;i ++){
        if (!used[i] && !dg[u+i] && !udg[n-u+i]){// 判断某列，对角线，反对角线是否用过
            // 判断对角线，反对角线用于剪枝
            g[u][i] = 'Q';// 在(u,i)处放置一个皇后
            used[i] = dg[u+i] = udg[n-u+i] = true;
            dfs(u+1);
            g[u][i] = '.';// 恢复现场
            used[i] = dg[u+i] = udg[n-u+i] = false;
        }
    }
}

int main(){
    IOS;
        
    cin >> n;
    
    for (int i = 0;i < n;i ++)// 初始化棋盘
        for (int j = 0;j < n;j ++) g[i][j] = '.';
        
    dfs(0);
    
    return 0;
}

时间复杂度：O(n^2*n!)，每次输出答案是O(n^2)，递归搜索是O(n!)。

算法2：DFS按每个元素枚举。递归实现指数型枚举。

从(0,0)一直搜索到(n-1,n-1)，对于每个位置，有放和不放皇后2种情况。

#include <iostream>
using namespace std;
#define IOS \
    ios::sync_with_stdio(false); \
    cin.tie(0); \
    cout.tie(0)
const int N = 10;// 对角线数量是2*n-1
bool row[N],col[N],dg[2*N],udg[2*N];// 判断某行，列，对角线，反对角线是否用过
char g[N][N];
int n;

void dfs(int x,int y,int s){
    if (s > n) return;// 剪枝优化
    if (y == n) y = 0,x ++;// 纵坐标走到头，从下一行第一列继续搜索
    
    if (x == n){
        if (s == n){// 走到最后一行且放完n个皇后输出答案
            for (int i = 0;i < n;i ++){
                for (int j = 0;j < n;j ++) cout << g[i][j];
                cout << '\n';
            }
            cout << '\n';
        }
        return;
    }
    
    // 不放皇后
    g[x][y] = '.';
    dfs(x,y+1,s);
    // 放皇后
    // 判断是否能放皇后
    if (!row[x] && !col[y] && !dg[x+y] && !udg[y-x+n] && x < n && y < n){
        row[x] = col[y] = dg[x+y] = udg[y-x+n] = true;
        g[x][y] = 'Q';
        dfs(x,y+1,s+1);// 可以写成dfs(x+1,0,s+1);优化，直接从下一行开始搜索
        row[x] = col[y] = dg[x+y] = udg[y-x+n] = false;// 恢复现场
        g[x][y] = '.';
    }
}

int main(){
    IOS;
        
    cin >> n;
        
    dfs(0,0,0);
    
    return 0;
}

时间复杂度：$O(2^{n^{2}})$，每个位置都有两种情况，总共有 n^2 个位置。