例题:897. 最长公共子序列(模板题)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| 给定两个长度分别为 N 和 M 的字符串 A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
输入格式
第一行包含两个整数 N 和 M。
第二行包含一个长度为 N 的字符串,表示字符串 A。
第三行包含一个长度为 M 的字符串,表示字符串 B。
字符串均由小写字母构成。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N,M≤1000
输入样例:
4 5
acbd
abedc
输出样例:
3
|
最长公共子序列,英文缩写为LCS(Longest Common Subsequence)。其定义是,一个序列 S ,如果分别是两个或多个已知序列的子序列,且是所有符合此条件序列中最长的,则 S 称为已知序列的最长公共子序列。
LCS也是一个非常经典的DP问题。
算法思路:
涉及到两个字符串序列的问题,DP做法的状态表示考虑序列1的前i个字母构成的序列,序列2的前j个字母构成的序列。
求序列x和序列y的LCS也就是处理x[1...i]和y[1...j]的LCS。
参考:《算法训练营》。
题解: https://www.acwing.com/solution/content/8111/。
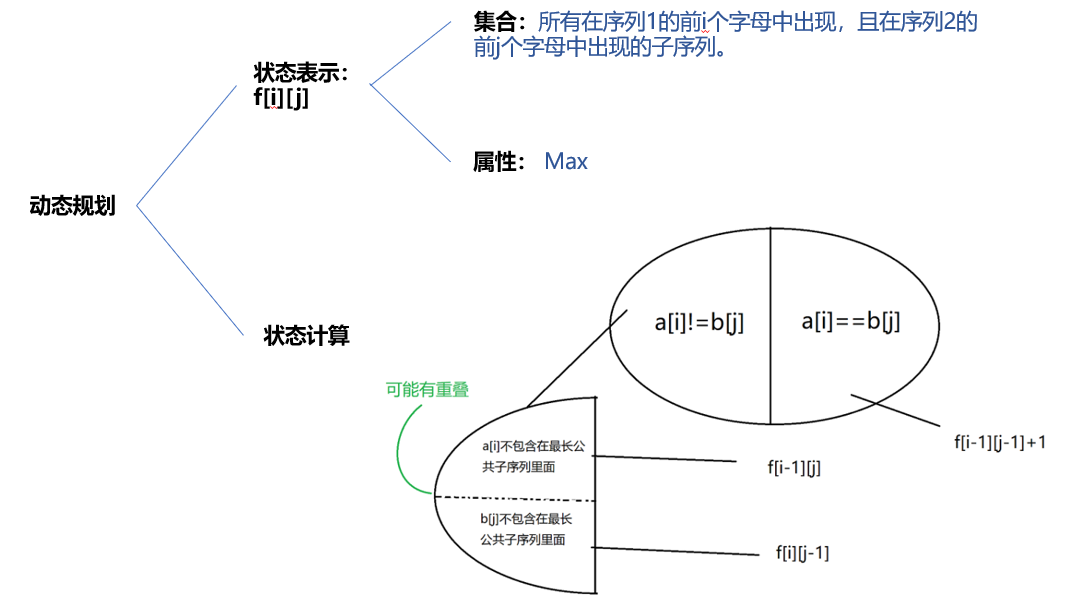
说明:对于状态的重复问题,由于状态属性是求Max值,所以重复无影响,这里可以重复但不能遗漏。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| import java.util.Scanner;
public class Main {
public static void main(String[] args) throws Exception {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int[][] dp = new int[n+5][m+5];
String a = " " + scan.next();
String b = " " + scan.next();
scan.close();
for (int i = 1;i <= n;i ++){
for (int j = 1;j <= m;j ++){
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
if (a.charAt(i) == b.charAt(j))
dp[i][j] = Math.max(dp[i][j], dp[i-1][j-1] + 1);
}
}
System.out.println(dp[n][m]);
}
}
|
4.3:区间DP
区间DP在蓝桥杯(三五)、(三六)已经介绍过了。
例题:282. 石子合并(模板题)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| 设有 N 堆石子排成一排,其编号为 1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有 4 堆石子分别为 1 3 5 2, 我们可以先合并 1、2 堆,代价为 4,得到 4 5 2, 又合并 1,2 堆,代价为 9,得到 9 2 ,再合并得到 11,总代价为 4+9+11=24;
如果第二步是先合并 2,3 堆,则代价为 7,得到 4 7,最后一次合并代价为 11,总代价为 4+7+11=22。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入格式
第一行一个数 N 表示石子的堆数 N。
第二行 N 个数,表示每堆石子的质量(均不超过 1000)。
输出格式
输出一个整数,表示最小代价。
数据范围
1≤N≤300
输入样例:
4
1 3 5 2
输出样例:
22
|
相邻的石子堆才能合并,石子合并有不同的顺序,每种顺序代价不一样,求最小代价。
具有明显的阶段性(相邻的合并),所以只能区间dp,不能贪心。
很棒的区间DP题解: https://www.acwing.com/solution/content/13945/。
区间DP的过程:
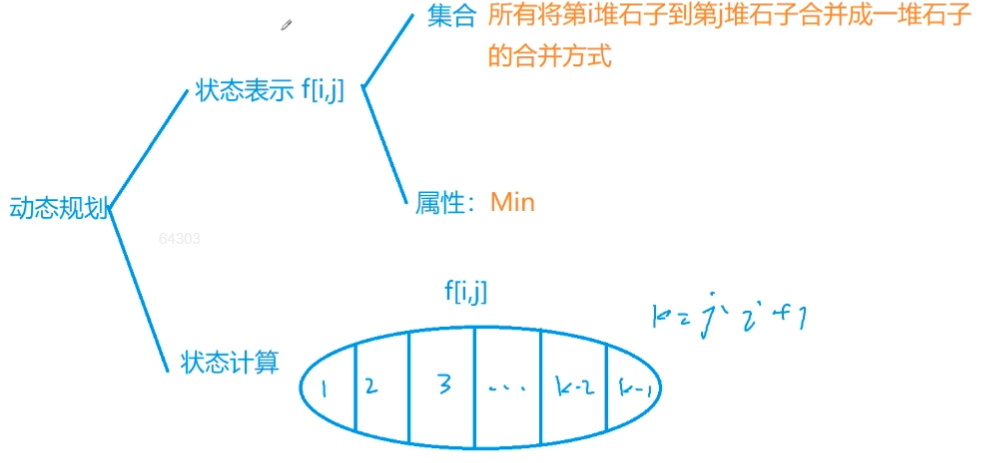
第一维都是枚举区间长度,一般 len = 1 用来初始化,枚举从 len = 2 开始,第二维枚举起点 i (右端点 j 自动获得,j = i + len - 1);
先求长度为1的DP区间,再求长度为2的,以此类推,由递推关系:长度为i+1的DP区间通过长度为i的DP区间求得;
对于每个DP区间dp[i][j],利用k作为分割点,也就是枚举从i到j的石堆合并成整体的最后一步合并的合并方法。k = l时,将k+1到r看作整体,与第l堆合并;k = l+1时,将l到k看作整体,将k+1到r看作整体,将它们合并。计算dp[l][r]时,需要用到的dp[l][k]和dp[k+1][r]都已经计算过了,所以算法是正确的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| import java.util.Scanner;
public class Main {
public static void main(String[] args) throws Exception {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[] a = new int[n+5];
int[] s = new int[n+5];
int[][] dp = new int[n+5][n+5];
for (int i = 1;i <= n;i ++){
a[i] = scan.nextInt();
}
scan.close();
for (int i = 1;i <= n;i ++) a[i] += a[i-1];
for (int len = 2;len <= n;len ++){
for (int l = 1;l + len - 1 <= n;l ++){
int r = l + len - 1;
dp[l][r] = 0x3f3f3f3f;
for (int k = l;k < r;k ++){
dp[l][r] = Math.min(dp[l][r],dp[l][k] + dp[k+1][r] + a[r] - a[l-1]);
}
}
}
System.out.println(dp[1][n]);
}
}
|
4.4:习题
例题:902. 最短编辑距离(模板题)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| 给定两个字符串 A 和 B,现在要将 A 经过若干操作变为 B,可进行的操作有:
删除–将字符串 A 中的某个字符删除。
插入–在字符串 A 的某个位置插入某个字符。
替换–将字符串 A 中的某个字符替换为另一个字符。
现在请你求出,将 A 变为 B 至少需要进行多少次操作。
输入格式
第一行包含整数 n,表示字符串 A 的长度。
第二行包含一个长度为 n 的字符串 A。
第三行包含整数 m,表示字符串 B 的长度。
第四行包含一个长度为 m 的字符串 B。
字符串中均只包含大写字母。
输出格式
输出一个整数,表示最少操作次数。
数据范围
1≤n,m≤1000
输入样例:
10
AGTCTGACGC
11
AGTAAGTAGGC
输出样例:
4
|
DP问题分析总结:状态计算往往以最后一步的选择方式进行划分,然后根据状态属性计算。
本题还是有难度的,思路比较独特,边界初始化很特殊。
y总思路太强了!!!
参考优秀题解: https://www.acwing.com/solution/content/5607/。
1
2
3
4
5
6
7
8
9
10
11
12
13
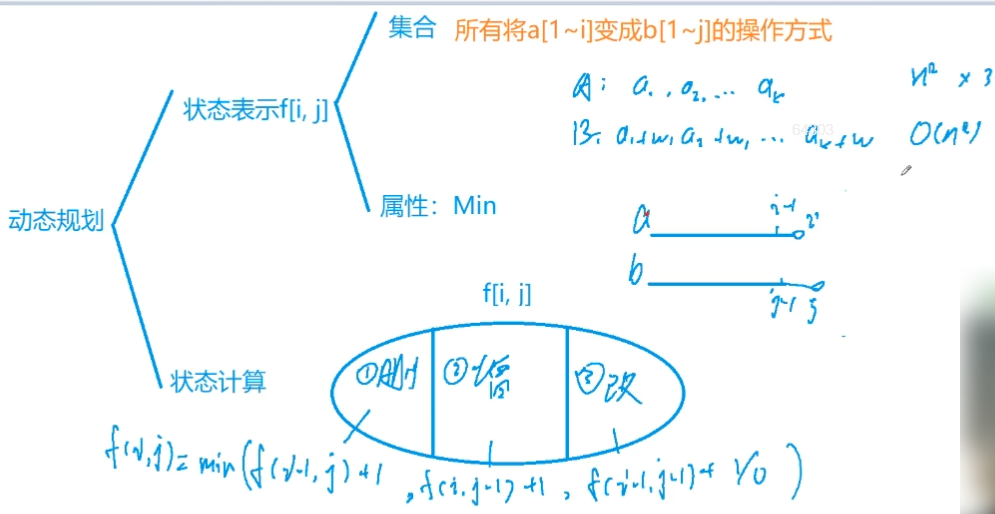
| 1)删除操作:把a[i]删掉之后a[1~i]和b[1~j]匹配
所以之前要先做到a[1~(i-1)]和b[1~j]匹配
f[i-1][j] + 1
2)插入操作:插入之后a[i]与b[j]完全匹配,所以a中插入的就是b[j]
那填之前a[1~i]和b[1~(j-1)]匹配
f[i][j-1] + 1
3)替换操作:把a[i]改成b[j]之后想要a[1~i]与b[1~j]匹配
那么修改这一位之前,a[1~(i-1)]应该与b[1~(j-1)]匹配
f[i-1][j-1] + 1
但是如果本来a[i]与b[j]这一位上就相等,那么不用改,即
f[i-1][j-1] + 0
好的那么f[i][j]就由以上三个可能状态转移过来,取个min
|
1
2
3
4
5
6
7
8
9
10
11
| 关于边界初始化问题:
先考虑有哪些初始化嘛
1.你看看在for遍历的时候需要用到的但是你事先没有的
(往往就是什么0啊1啊之类的)就要预处理
2.如果要找min的话别忘了INF
要找有负数的max的话别忘了-INF
ok对应的:
1.f[0][i] = i如果a初始长度就是0,那么只能用插入操作让它变成b
f[i][0] = i同样地,如果b的长度是0,那么a只能用删除操作让它变成b
2.f[i][j] = INF
|
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include <iostream>
#include <algorithm>
using namespace std;
#define IOS \
ios::sync_with_stdio(false); \
cin.tie(0); \
cout.tie(0)
const int N = 1010,INF = 0x3f3f3f3f;
int n,m;
char a[N],b[N];
int dp[N][N];
int main(){
IOS;
cin >> n;
for (int i = 1;i <= n;i ++) cin >> a[i];
cin >> m;
for (int i = 1;i <= m;i ++) cin >> b[i];
for (int i = 1;i <= n;i ++)
for (int j = 1;j <= m;j ++)
dp[i][j] = INF;
for (int i = 0;i <= n;i ++) dp[i][0] = i;
for (int i = 0;i <= m;i ++) dp[0][i] = i;
for (int i = 1;i <= n;i ++)
for (int j = 1;j <= m;j ++){
dp[i][j] = min(dp[i-1][j] + 1,dp[i][j-1] + 1);
if (a[i] == b[j]) dp[i][j] = min(dp[i][j],dp[i-1][j-1]);
else dp[i][j] = min(dp[i][j],dp[i-1][j-1] + 1);
}
cout << dp[n][m] << '\n';
return 0;
}
|




