算法基础课笔记（二六）

例题：899. 编辑距离（模板题）

给定 n 个长度不超过 10 的字符串以及 m 次询问，每次询问给出一个字符串和一个操作次数上限。
对于每次询问，请你求出给定的 n 个字符串中有多少个字符串可以在上限操作次数内经过操作变成询问给出的字符串。
每个对字符串进行的单个字符的插入、删除或替换算作一次操作。

输入格式
第一行包含两个整数 n 和 m。
接下来 n 行，每行包含一个字符串，表示给定的字符串。
再接下来 m 行，每行包含一个字符串和一个整数，表示一次询问。
字符串中只包含小写字母，且长度均不超过 10。

输出格式
输出共 m 行，每行输出一个整数作为结果，表示一次询问中满足条件的字符串个数。

数据范围
1≤n,m≤1000,

输入样例：
3 2
abc
acd
bcd
ab 1
acbd 2
输出样例：
1
3

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
#define IOS \
    ios::sync_with_stdio(false); \
    cin.tie(0); \
    cout.tie(0)
const int M = 1010,N = 15,INF = 0x3f3f3f3f;
int n,m;
char str_n[M][N];
int dp[N][N];

int distance(char a[],char b[]){// 计算从a变换到b所用的最少操作数
    int la = strlen(a),lb = strlen(b);
    for (int i = 1;i <= la;i ++)
        for (int j = 1;j <= lb;j ++)
            dp[i][j] = INF;
    
    for (int i = 0;i <= la;i ++) dp[i][0] = i;
    for (int i = 0;i <= lb;i ++) dp[0][i] = i;

    for (int i = 1;i <= la;i ++)
        for (int j = 1;j <= lb;j ++){
            dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + 1;
            dp[i][j] = min(dp[i][j],dp[i-1][j-1] + (a[i-1] != b[j-1]));
        }
    return dp[la][lb];
}

int main(){
    IOS;
    
    cin >> n >> m;
    for (int i = 0;i < n;i ++) cin >> str_n[i];

    while (m --){// 处理询问
        char str_m[N];
        int limit;
        cin >> str_m >> limit;
        int res = 0;// 对于n个字符串，分别求最少操作数
        for (int i = 0;i < n;i ++){
            if (distance(str_n[i],str_m) <= limit) res ++;
        }
        cout << res << '\n';
    }
    return 0;
}

4.5：计数类DP

例题：900. 整数划分（模板题）

一个正整数 n 可以表示成若干个正整数之和，形如：n=n1+n2+…+nk，其中 n1≥n2≥…≥nk,k≥1。
我们将这样的一种表示称为正整数 n 的一种划分。
现在给定一个正整数 n，请你求出 n 共有多少种不同的划分方法。

输入格式
共一行，包含一个整数 n。

输出格式
共一行，包含一个整数，表示总划分数量。
由于答案可能很大，输出结果请对 10^9+7 取模。

数据范围
1≤n≤1000
输入样例:
5
输出样例：
7

之前讲的DP问题的状态属性都是最大/小值，本题求的是个数。

算法思路：

题目中要求n划分的数从大到小排序，所以是求组合的问题，不考虑排列。

算法1：完全背包写法

可以看成完全背包来处理，背包的体积是n，物品体积分别是1，2，3，…，n，数量无限制，所选物品体积必须恰好装满背包。

回顾完全背包问题的状态转移方程：f[i][j] = max(f[i-1][j],f[i][j-v[i]]+w[i])。

参考题解： https://www.acwing.com/solution/content/2954/。

状态计算：

f[i][j] 表示前i个整数（1,2…,i）恰好拼成j的方案数
求方案数：把集合选0个i，1个i，2个i，…全部加起来
f[i][j] = f[i - 1][j] + f[i - 1][j - i] + f[i - 1][j - 2 * i] + ...;
f[i][j - i] =           f[i - 1][j - i] + f[i - 1][j - 2 * i] + ...;
因此 f[i][j]=f[i−1][j]+f[i][j−i]; (这一步类似完全背包的推导）

初值问题：

求最大值时，当都不选时，价值显然是 0;
而求方案数时，当都不选时，方案数是 1（即前 i 个物品都不选的情况也是一种方案），所以需要初始化为 1
即：for (int i = 0; i <= n; i ++) f[i][0] = 1;
等价变形后： f[0] = 1

朴素写法：

#include <iostream>
#include <algorithm>
using namespace std;
#define IOS \
    ios::sync_with_stdio(false); \
    cin.tie(0); \
    cout.tie(0)
const int N = 1010,MOD = 1e9+7;
int n;
int dp[N][N];

int main(){
    IOS;
    cin >> n;

    for (int i = 0;i <= n;i ++) dp[i][0] = 1; // i必须从0开始枚举，容量为0时方案数都为1

    for (int i = 1;i <= n;i ++)
        for (int j = 0;j <= n;j ++){
            dp[i][j] = dp[i-1][j] % MOD;
            if (j >= i) dp[i][j] = (dp[i-1][j] + dp[i][j-i]) % MOD;
        }

    cout << dp[n][n] << '\n';
    return 0;
}

滚动数组空间优化：

int dp[N];
int main(){
    IOS;
    cin >> n;
    dp[0] = 1; // i必须从0开始枚举，容量为0时方案数都为1

    for (int i = 1;i <= n;i ++)
        for (int j = i;j <= n;j ++){
            dp[j] = (dp[j] + dp[j-i]) % MOD;
        }

    cout << dp[n] << '\n';
    return 0;
}

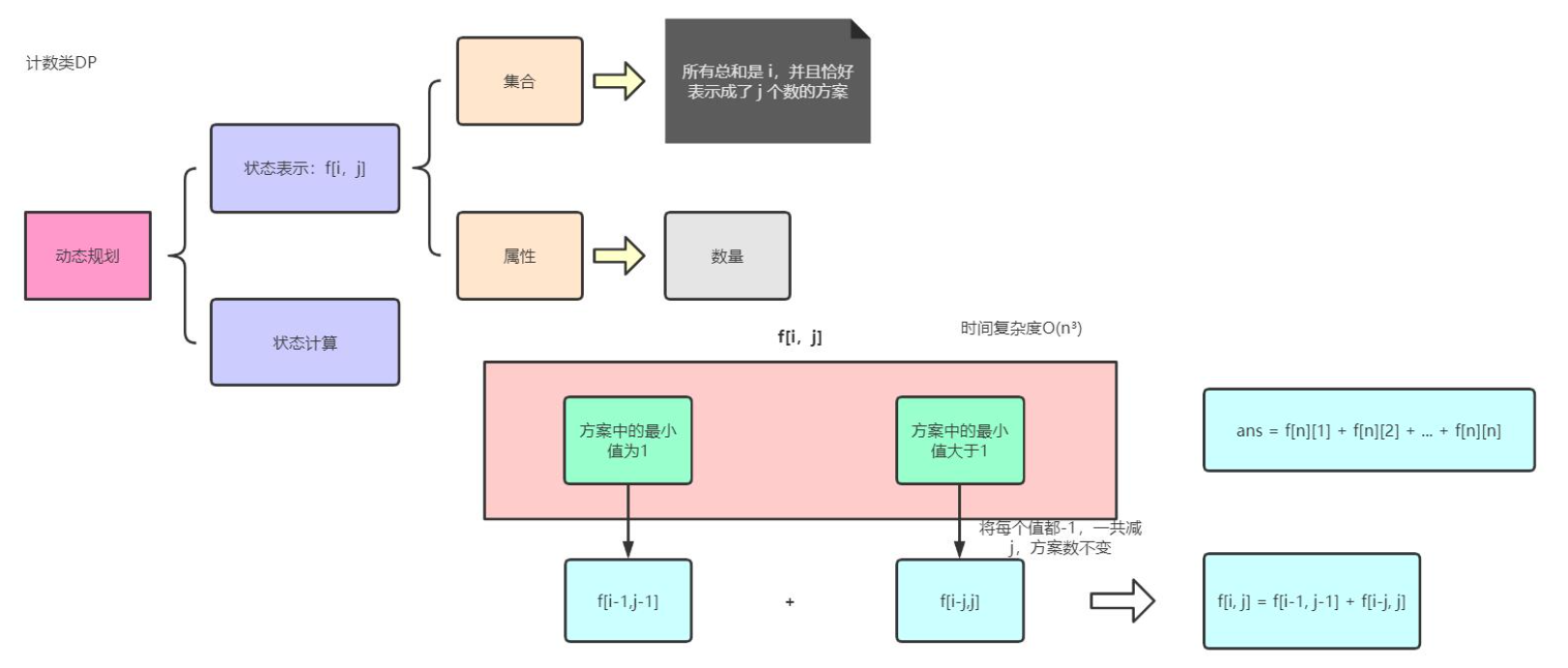
算法2：计数类DP

计数类DP的状态表示：算法思路更难想到。

将一个数i划分成j份，划分的最小单位是1，这可以作为状态计算的最后一步计算依据。

当方案中的最小值为1时，不妨将每个方案中减去一个数1，总方案数不变，等于f[i-1,j-1]。这些方案再加上一个数1，又变回来了，它们是一一对应的；
当方案中的最小值大于1时，不妨将每个方案中的每个数减去1，总方案数不变，等于f[i-j,j]。它们也是一一对应的。

这样就不难推导出状态转移方程，最后记得把f[n][i],i = 1,2,...,n累加，就是答案。

和前面的完全背包解法转移方程对比一下，会发现2种算法本质上是差不多的。

#include <iostream>
#include <algorithm>
using namespace std;
#define IOS \
    ios::sync_with_stdio(false); \
    cin.tie(0); \
    cout.tie(0)
const int N = 1010,MOD = 1e9+7;
int n;
int dp[N][N];

int main(){
    IOS;
    cin >> n;

    dp[0][0] = 1; // 0划分为0个数的方案数为1

    for (int i = 1;i <= n;i ++)
        for (int j = 1;j <= i;j ++){ // i最多划分为i个数
            dp[i][j] = (dp[i-1][j-1] + dp[i-j][j]) % MOD;
        }

    int res = 0; // 注意：不要写成 res += dp[n][i] % MOD了！！！
    for (int i = 1;i <= n;i ++) res = (res + dp[n][i]) % MOD;
    cout << res << '\n';
    return 0;
}