grant's Blog

记录生活中的点点滴滴

考研算法辅导课笔记（十五）

发表于 更新于 分类于 ， ，   阅读次数： Valine：
本文字数： 5.1k 阅读时长 ≈ 5 分钟

Quick Sort（快速排序）

算法原理详见： https://grant1499.github.io/posts/7ff5bb67.html。

算法思想：

  1. 选取一个数为基准（一般取第一个或最后一个或者中间的数）
  2. 将比基准小的数交换到前面，比基准大的数交换到后面
  3. 对左右区间重复第二步，直到各区间只有一个数

图片

image-20210724101609079

代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

注意这里的代码和笔试代码有不同的地方，注意区别。

image-20220112103040574

按照王道的代码，每轮排序后会将基准元素放到其最终位置上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// AC，样例通过：13/13
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N],n;

void quick_sort(int a[],int l,int r){
    if (l >= r) return; // 递归退出边界
    int i = l-1,j = r+1,x = a[l+r>>1]; // 基准点x取为中间点
    
    while (i < j){
        while (a[++i] < x); // 指针i从左往右找到>= x的位置
        while (a[--j] > x); // 指针j从右往左找到<= x的位置
        if (i  < j) swap(a[i],a[j]); // 交换位置
    }
    
    quick_sort(a,l,j),quick_sort(a,j+1,r); // 递归处理
}

int main(){
    cin >> n;
    
    for (int i = 0;i < n;i ++) cin >> a[i];
    
    quick_sort(a,0,n-1);
    
    for (int i = 0;i < n;i ++) cout << a[i] << ' ';
    return 0;
}

效率分析：

1.最好时间复杂度：$O(n*log n)$。

每一轮划分都以中位数为基准，递归大概进行log n层。

2.平均时间复杂度：$O(n*log n)$。

递归的平均执行层数是log n层。

3.最坏时间复杂度：$O(n^2)$。

每一轮划分以最小/大值为基准，分为1和n-1两组，执行n^2次。

快排极少会退化到$O(n^2)$，基本不用考虑。

4.稳定性：不稳定排序。

5.空间复杂度：$O(n*log n)$。

递归调用系统栈，一般指平均值。

拓展题目：

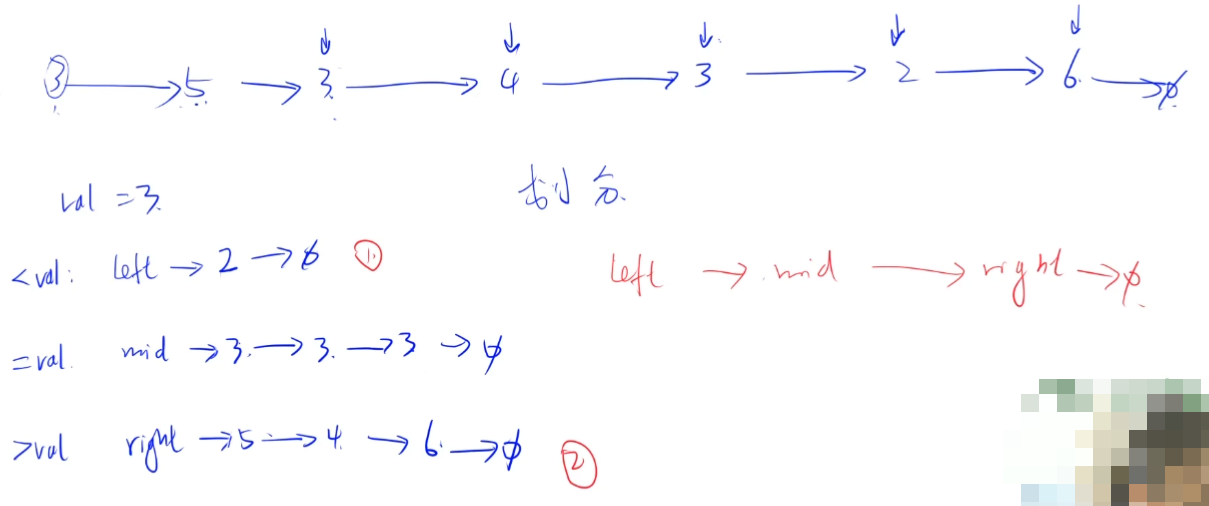
*acwing.1451. 单链表快速排序

1
2
3
4
5
6
7
8
9
10
11
给定一个单链表，请使用快速排序算法对其排序。
要求：期望平均时间复杂度为 O(nlogn)，期望额外空间复杂度为 O(logn)。
思考题： 如果只能改变链表结构，不能修改每个节点的val值该如何做呢？

数据范围
链表中的所有数大小均在 int 范围内，链表长度在 [0,10000]。

输入样例：
[5, 3, 2]
输出样例：
[2, 3, 5]

链表快排其实比数组快排更好些，数组快排边界处理比较麻烦。

思路：

image-20220112213637333

将整个链表划分为left，mid，right三个子链表后，再递归处理left和right链表。

然后把left，mid，right子链表从左到右拼接起来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* get_tail(ListNode* head){
        while (head->next) head = head->next;
        return head;
    }

    ListNode* quickSortList(ListNode* head) {
        if (!head || !head->next) return head; // 递归边界
        // 定义三个子链表的虚拟头节点，以及三个尾指针，方便尾插
        auto left = new ListNode(-1),mid = new ListNode(-1),right = new ListNode(-1);
        auto ltail = left,mtail = mid,rtail = right;
        
        int val = head->val; // 以第一个节点val为基准
        for (auto p = head; p; p = p->next){
            if (p->val < val) ltail = ltail->next = p;
            if (p->val == val) mtail = mtail->next = p;
            if (p-> val > val) rtail = rtail->next = p;
        }
        
        ltail->next = mtail->next = rtail->next = NULL; // 记得子链表尾部指向NULL
        // 递归left和right链表，left->next才有数据
        left->next = quickSortList(left->next); 
        right->next = quickSortList(right->next);
        // 拼接三个子链表
        get_tail(left)->next = mid->next; // 用left的尾部接上mid的数据部分
        // mid链表可能不存在，所以还要用到left的尾部
        get_tail(left)->next = right->next;
        
        auto p = left->next;
        delete left; // 释放虚拟头节点
        delete mid;
        delete right;
        return p;
    }
};

Heap Sort（堆排序）

堆是一棵完全二叉树。

算法原理详见： https://grant1499.github.io/posts/2a91527b.html。

代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

代码以大根堆为例。（小根堆是一样的，见算法基础课）

大根堆定义：每个节点的键值大于或等于左右孩子，堆顶就是整个堆的最大值。

堆一般采用顺序存储，比链式存储效率高不少，因为要用到索引操作。

编号从1开始，则编号为x的左孩子为2x，右孩子为2x+1，父节点为：$\lfloor x/2 \rfloor$。

建堆：时间复杂度，O(n)。证明见算法基础课。

从倒数第2层直到最上层执行down操作，向下调整建堆。

倒数第2层节点数约n/4，往下down 1层；倒数第3层节点数约n/8，往下down 2层；……

总时间复杂度约为：n/4 * 1+ n/8 * 2 + n/16 * 3 + ... = O(n)。

之所以能O(n)建堆，是因为堆性质很弱，二叉堆并不是唯一的。

向下调整down：时间复杂度，$O(log n)$。完全二叉树的层数约为log n。

在该结点的儿子中，找一个最小的，与该结点交换，重复此过程直到底层。

向上调整类似。可用迭代或者递归实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// AC，样例通过：13/13
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N],n;

void down(int a[],int u,int len){
    int t = u;
    if (2*u <= len && a[2*u] > a[t]) t = 2*u;
    if (2*u+1 <= len && a[2*u+1] > a[t]) t = 2*u+1;
    if (t != u){
        swap(a[u],a[t]);
        down(a,t,len);
    }
}

void heap_sort(int a[],int n){
    int len = n; // len维护堆的大小，范围：1~len
    for (int i = n/2; i; i --) down(a,i,len); // 建堆
    
    for (int i = 0;i < n-1;i ++){ // n-1轮，每一轮操作找到最大的一个数
         // 注意顺序不要写反，先把堆顶换下来，然后删掉末尾，down堆顶
        swap(a[1],a[len]);
        len --;
        down(a,1,len);
    }
}

int main(){
    cin >> n;
    
    for (int i = 1;i <= n;i ++) cin >> a[i]; // 注意下标从1开始
    
    heap_sort(a,n);
    
    for (int i = 1;i <= n;i ++) cout << a[i] << ' ';
    return 0;
}

效率分析：

1.最好时间复杂度：$O(n*log n)$。

2.平均时间复杂度：$O(n*log n)$。

3.最坏时间复杂度：$O(n*log n)$。

背过就行。

4.稳定性：不稳定排序。

堆顶和堆尾元素存在交换，会导致不稳定。

Merge Sort（二路归并排序）

算法原理详见： https://grant1499.github.io/posts/7ff5bb67.html。

算法思想：

  1. 把长度为n的输入序列分成两个长度为n/2的子序列；

  2. 对这两个子序列分别采用归并排序；

  3. 将两个排序好的子序列合并成一个最终的排序序列。

图片

代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// AC，样例通过：13/13
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N],temp[N],n; // 归并需要一个临时数组

void merge_sort(int a[],int l,int r){
    if (l >= r) return;
    int mid = l + r >> 1;
    int i = l,j = mid + 1,k = 0;
    
    merge_sort(a,i,mid),merge_sort(a,j,r); // 先递归再归并
    while (i <= mid && j <= r){
        if (a[i] <= a[j]) temp[k++] = a[i++]; // 取 <= 保证稳定性
        else temp[k++] = a[j++];
    }
    
    while (i <= mid) temp[k++] = a[i++];
    while (j <= r) temp[k++] = a[j++];
    
    for (int i = 0,j = l;j <= r;i ++,j ++) a[j] = temp[i];
}

int main(){
    cin >> n;
    
    for (int i = 0;i < n;i ++) cin >> a[i];
    
    merge_sort(a,0,n-1);
    
    for (int i = 0;i < n;i ++) cout << a[i] << ' ';
    return 0;
}

效率分析：

1.最好时间复杂度：$O(n*log n)$。

2.平均时间复杂度：$O(n*log n)$。

3.最坏时间复杂度：$O(n*log n)$。

二路归并每次都将数组分为一半，大概执行O(log n)层。

4.稳定性：稳定排序。

5.空间复杂度：O(n)。

需要一个额外的临时数组。

快排与归并的区别：

快排：先处理，再递归。（尾递归，可以转化为迭代写法）

归并：先递归，再处理。

快排递归划分的期望是O(logn)，而归并递归划分一定是O(logn)。

坚持原创技术分享，您的支持将鼓励我继续创作！