grant's Blog

记录生活中的点点滴滴

考研算法辅导课笔记（十六）

发表于 更新于 分类于 ， ，   阅读次数： Valine：
本文字数： 6.1k 阅读时长 ≈ 6 分钟

第十二讲 桶排序、基数排序、外部排序

  1. 桶排序
    (1) 时间复杂度
     a. 最好情况：O(n + m)
 b. 平均情况：O(n + m)
 c. 最坏情况：O(n + m)
    (2) 空间复杂度
     O(n + m)
    (3) 稳定
  2. 基数排序
    (1) 时间复杂度
     a. 最好情况：O(d(n + r))
 b. 平均情况：O(d(n + r))
 c. 最坏情况：O(d(n + r))
    (2) 空间复杂度
     O(n + r)
    (3) 稳定

排序算法分类

常见的排序算法一般分为以下两种：

（1）比较类排序

（2）非比较类排序

前面提到过的排序算法都是基于比较的排序算法。

比较类排序指将待排序的元素两两比较，满足一定条件时交换位置，直到排序完成为止。而非比较类排序则不涉及元素之间的比较，而是将元素按照一定类别分类，最后将不同的类别按大小顺序接在一起以完成排序。

可以证明没有比nlogn更快的比较类排序算法。即，比较类排序的时间复杂度下限为nlogn。

参考文章： https://zhuanlan.zhihu.com/p/387612122。

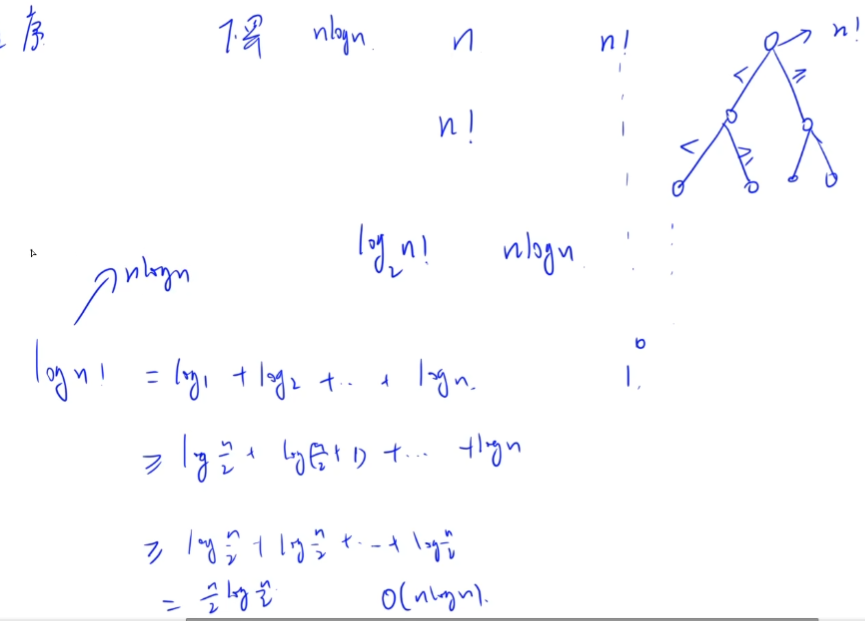
image-20220112115134456

对一个长度为N的数组，其中元素共有N！种不同的组合形式。排序结束情况为其中一种。

由于基于比较的排序需要在两个元素a,b之间进行比较。每一次比较只有a>b或a<b两种可能性。比较完一次可过滤掉一半的错误可能。即为1/2*N!种可能性。

每经过一次比较即可再过滤掉一半可能性。假设经过k次比较，得到了唯一的最终答案。

image-20220112115244948

上下一夹逼就能证明比较类排序的时间复杂度下限为nlogn。

* Bucket Sort（桶排序）& Counting Sort（计数排序）

注：考研408数据结构不涉及桶排序和计数排序。

Bucket Sort（桶排序）

适用于待排序数据值域较大但分布比较均匀的情况。

将值为i的元素放入i号桶，最后依次把桶里的元素倒出来。

算法思想：

  1. 设置一个定量的数组当作空桶子。
  2. 寻访序列，并且把项目一个一个放到对应的桶子去。
  3. 对每个不是空的桶子进行排序。
  4. 从不是空的桶子里把项目再放回原来的序列中。

桶.gif

如果使用稳定的内层排序，并且将元素插入桶中时不改变元素间的相对顺序，那么桶排序就是一种稳定的排序算法。

由于每块元素不多，一般使用插入排序。此时桶排序是一种稳定的排序算法。

时间复杂度：

最好 — O(n+k)

最坏 — O(n^2)

平均 — O(n+k)

注： 其中k=nlog(n/m)

代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

参考文章： https://www.acwing.com/blog/content/8989/。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// 样例通过：11/13
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 100010;
int a[N],n;

void bucket_sort(int a[], int n){
    int minval = a[0], maxval = a[0];
    for(int i = 0; i < n; i ++){//寻找原序列数组元素的最大值和最小值 
        minval = min(minval, a[i]);
        maxval = max(maxval, a[i]);
    }

    int bnum = 10;//桶中元素个数 
    int m = (maxval - minval) / bnum + 1;//桶的个数 
    vector< vector<int> > bucket(m);

    //收集,将元素入相应的桶中. 减偏移量是为了将元素映射到更小的区间内,省内存 
    for(int i = 0; i < n; i ++) bucket[(a[i] - minval) / bnum].push_back(a[i]);

    //将桶内元素排序 
    for(int i = 0; i < m; i ++) sort(bucket[i].begin(), bucket[i].end());

    //收集, 将各个桶中的元素收集到一起 
    for(int i = 0, k = 0; i < m; i ++){
        for(int j = 0; j < bucket[i].size(); j ++){
            a[k++] = bucket[i][j];
        }
    }
}

int main(){
    cin >> n;
    
    for (int i = 0;i < n;i ++) cin >> a[i];
    
    bucket_sort(a,n);
    
    for (int i = 0;i < n;i ++) cout << a[i] << ' ';
    return 0;
}

Counting Sort（计数排序）

计数排序本质上是一种特殊的桶排序，当桶的个数最大的时候，就是计数排序。

计数排序基于一个假设，待排序数列的所有数均为整数，且出现在（0，k）的区间之内。

如果 k（待排数组的最大值） 过大则会引起较大的空间复杂度，一般是用来排序 0 到 100 之间的数字的最好的算法，但是它不适合按字母顺序排序人名。

算法思想：

  1. 找出待排序的数组中最大和最小的元素；
  2. 统计数组中每个值为 i 的元素出现的次数，存入数组 C 的第 i 项；
  3. 对所有的计数累加（从 C 中的第一个元素开始，每一项和前一项相加）；
  4. 向填充目标数组：将每个元素 i 放在新数组的第 C[i] 项，每放一个元素就将 C[i] 减去 1。

图片

image-20220112120332929

对于每个ai最终的排位，我们可以直接计算出来，而不需要比较。

它的排序取决于小于ai的元素个数，加上初始时在ai左边且等于ai的元素个数。

小于ai的元素个数可以通过计算桶中元素的前缀和快速求出来。

如果有重复元素如何计算？（Sx 表示 <= x 的元素的个数）

我们先考虑重复元素中在初始时位置最靠后的元素 x（以上图为例），

它的最终排位应该是S{x-1} + 3 = Sx - 1。

然后再看倒数第二个x， 它的最终排位应该是S{x-1} + 2 = Sx - 2。

时间复杂度：O(n+m)，n为元素个数，m为桶个数。

代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

y总的计数排序写法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 样例通过：10/13
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10000010;
int a[N],w[N],s[N],n; // s[N]是表示N个桶，同时维护前缀和，w[N]是排名数组

void counting_sort(int a[],int n){
    for (int i = 0;i < n;i ++) s[a[i]] ++; // s[k]表示数值等于k的元素个数
    for (int i = 1;i < N;i ++) s[i] += s[i-1]; // 桶的个数取决于数据范围
    // 逆序处理，再加上 -1 操作，以保证稳定性
    for (int i = n-1;i >= 0;i --) w[-- s[a[i]]] = a[i]; // 计算a[i]的最终排名
    for (int i = 0;i < n;i ++) a[i] = w[i]; // 根据排名重新整理a数组
}

int main(){
    cin >> n;
    
    for (int i = 0;i < n;i ++) cin >> a[i];
    
    counting_sort(a,n);
    
    for (int i = 0;i < n;i ++) cout << a[i] << ' ';
    return 0;
}

Radix Sort（基数排序）

一种非比较型的排序算法，最早用于解决卡片排序的问题。

一种多关键字的排序算法，可用桶排序实现。

算法思想：

  1. 取得数组中的最大数，并取得位数；
  2. arr为原始数组，从最低位开始取每个位组成radix数组；
  3. 对radix进行计数排序（利用计数排序适用于小范围数的特点）

图片

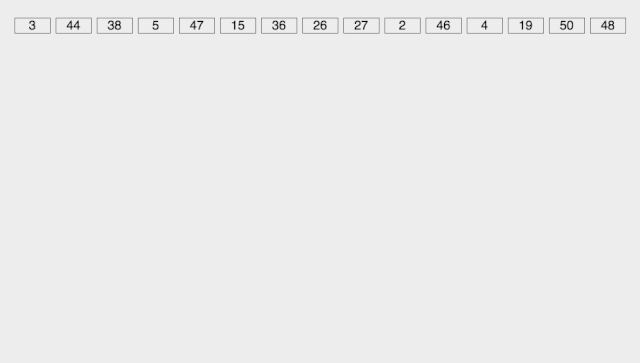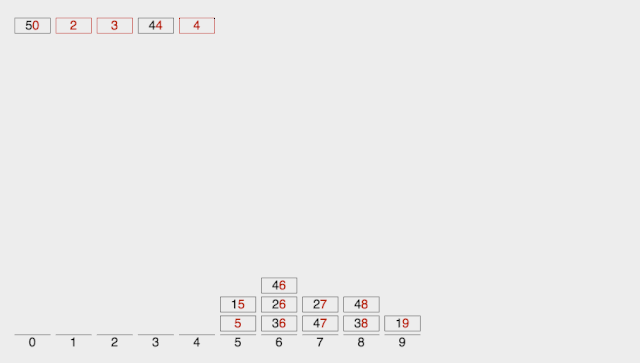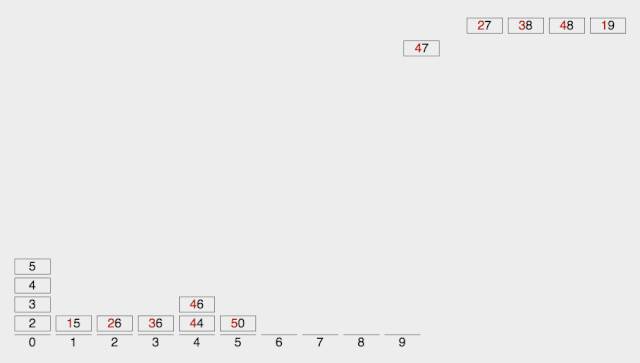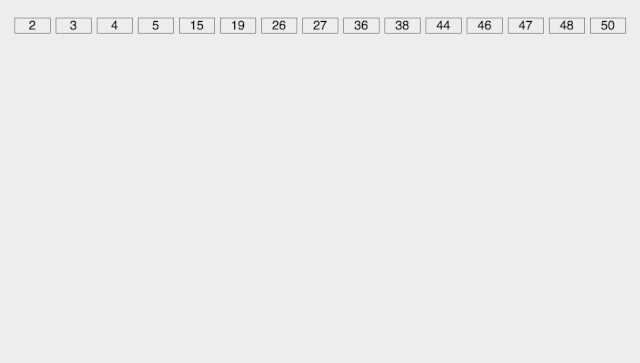
代码实现：

题目链接：https://www.acwing.com/problem/content/description/787/。

基数排序，基数指的是进制中的基数。

将要排序的十进制元素转化为r进制数组，对数组的每一位按多关键字排序。

对于每个关键字，位数不超过d位，范围是0~r-1，所以可以利用计数排序将时间复杂度控制到线性。

实现多关键字排序通常有两种方法：

  1. 最高位优先法（MSD）：优先比较高位，需要递归处理
  2. 最低位优先法（LSD）：优先比较低位
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// AC，样例通过：13/13
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 100010;
int a[N],s[N],w[N],n;

void radix_sort(int d,int r){ // 10进制数转化为不超过d位的r进制数
    int radix = 1;
    for (int i = 1;i <= d;i ++){ // 从低位到高位进行多关键字排序
        for (int j = 0;j < r;j ++) s[j] = 0; // 清空所有桶
        // a[j] / radix % r，取a[j]的最低位
        for (int j = 0;j < n;j ++) s[a[j] / radix % r] ++;
        for (int j = 1;j < r;j ++) s[j] += s[j-1]; // 单关键字的范围是：0~r-1
        
        for (int j = n-1;j >= 0;j --) w[-- s[a[j] / radix % r]] = a[j];
        for (int j = 0;j < n;j ++) a[j] = w[j];
        radix *= r;
    }
}

int main(){
    cin >> n;
    
    for (int i = 0;i < n;i ++) cin >> a[i];
    
    radix_sort(10,10); // radix_sort(4,1000)更快一点
    
    for (int i = 0;i < n;i ++) cout << a[i] << ' ';
    return 0;
}

时间复杂度：O(d*(n+r))。原始数组每个元素转化为r进制数后最多有d位。

空间复杂度：O(r)（王道写法）。需要r个桶加上排名数组的辅助空间，实际上是O(n+r)。

由于计数排序是稳定排序，所以基数排序也是稳定排序。

外部排序算法

(1) 置换选择排序

(2) 归并排序

a. 胜者树

b. 败者树

c. huffman树

前面介绍过的排序算法都属于内部排序算法，是在内存中进行的。

在许多应用中需要对大文件进行排序，用到外部排序算法，在外存中进行。

大文件无法整个复制进内存中排序，所以需要将数据部分调入内存排序，整个过程中需要多次进行内存和外存间的交换。

内部排序算法的时间瓶颈主要在比较次数，而外部排序算法的时间瓶颈主要在读写磁盘次数。

外部排序常用归并排序算法。

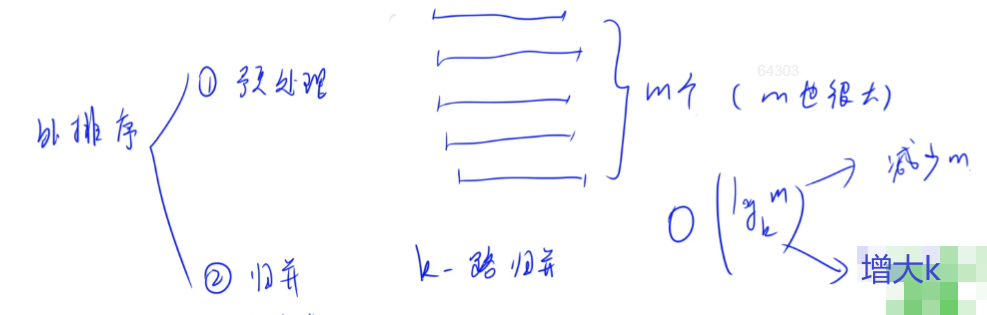
image-20220112151146419

对m个有序序列执行k-路归并，总共需要$O(log_k m)$轮排序。

针对两种效率改进思路，我们有两类算法。

置换选择排序

参考视频： https://www.bilibili.com/video/BV1b7411N798?p=89。（王道数据结构，很清楚）

置换选择排序，用于生成初始归并段，就是减少m的策略。

减少归并段的数量，也就是延长每个归并段的长度。

image-20220112154410850

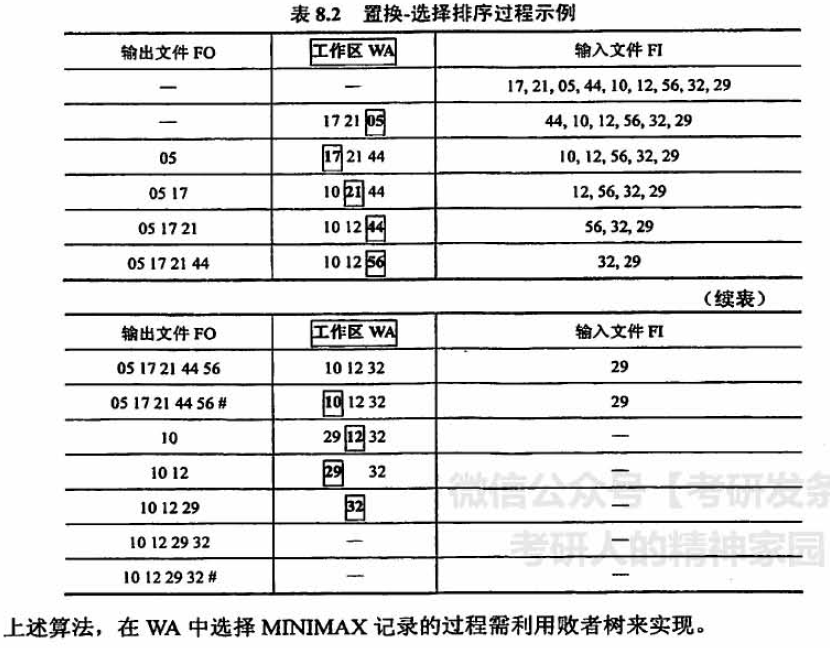
image-20220112154455554

置换选择排序选择MINIMAX记录可以用堆或者败者树维护。

胜者树与败者树

参考文章： https://blog.csdn.net/whz_zb/article/details/7425152。

参考视频： https://www.bilibili.com/video/BV1b7411N798?p=88。（王道数据结构）

胜者树和败者树都是完全二叉树，是树形选择排序（锦标赛排序）的一种变型。每个叶子结点相当于一个选手，每个中间结点相当于一场比赛，每一层相当于一轮比赛。

不同的是，胜者树的中间结点记录的是胜者的标号；而败者树的中间结点记录的败者的标号。

胜者树与败者树可以在log(n)的时间内找到最值。任何一个叶子结点的值改变后，利用中间结点的信息，还是能够快速地找到最值。在k路归并排序中经常用到。

堆也是完全二叉树。可以发现胜者树与败者树也满足堆的性质。

如果采用堆来维护最小值，输出当前最小值后，需要将堆尾移到堆顶然后执行down操作，再将新增元素插入堆尾然后执行up操作。

如果采用胜者树来维护最小值，输出当前最小值（胜者）后，只需要将新增元素取代当前最小值的位置，然后执行up操作（进行比赛直到选出冠军）。

两者对比，堆需要一轮down+up操作，胜者树需要一轮up操作。（败者树也只需要一轮up操作）

胜者树：

注：王道数据结构并未提到胜者树，408应该也不会考察，直接掌握败者树就行。

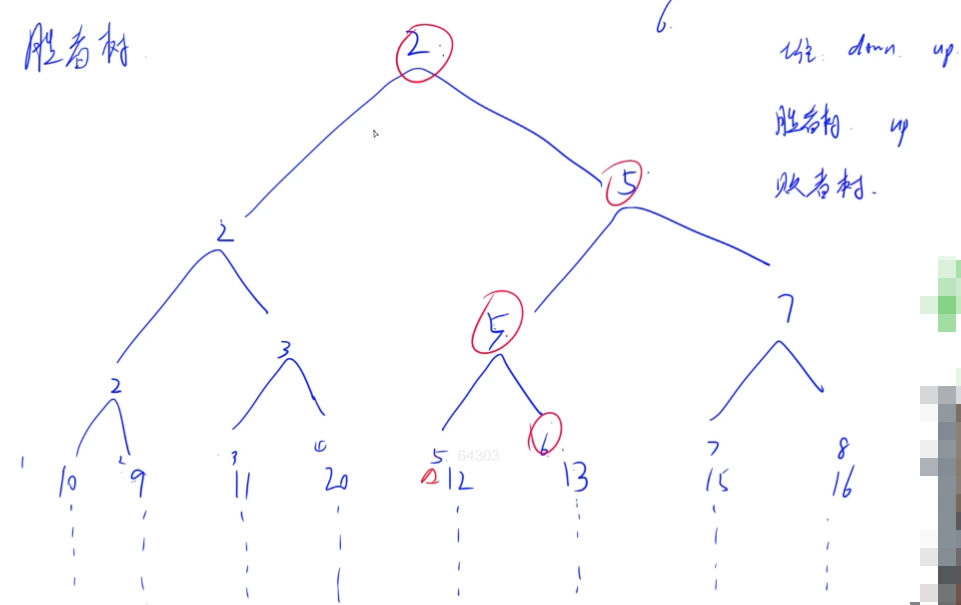
image-20220112170453743

胜者树在选出新一轮胜者时，需要将新增元素执行up操作，不仅需要访问本轮胜者的路径上所有节点，还要和它们的兄弟节点比较。

比如上图中的13是新增元素，13需要和兄弟12比较，12胜出后还需要和15比较。

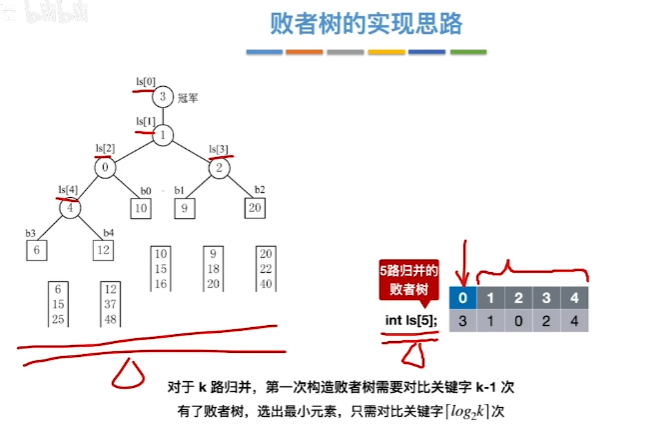
败者树：

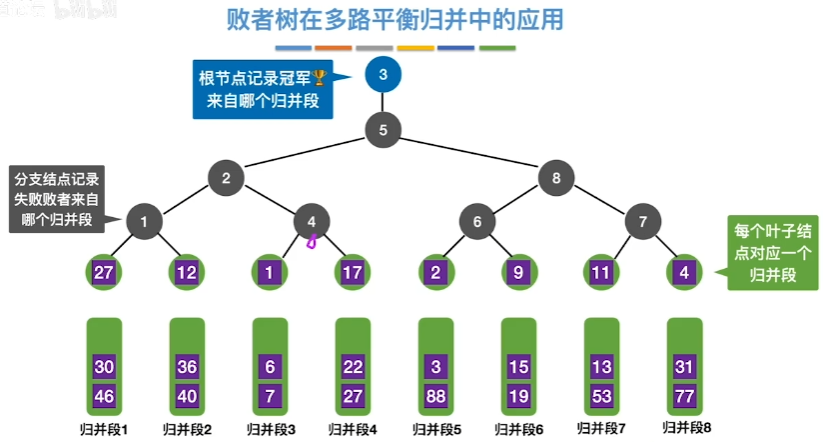
image-20220112161947706

败者树是对胜者树的进一步改进。它可以避免访问路径上的节点的兄弟节点，只需要和路径上所有节点比较。

败者树简化了重构。败者树的重构只是与该结点的父结点的记录有关，而胜者树的重构还与该结点的兄弟结点有关。败者树将胜者树选出新胜者的访问节点次数减少到一半，常数级优化。

上图的败者树中的非叶节点记录的是归并段的编号。

对于k-路归并，利用败者树归并k个归并段，选出最小元素需要的比较次数为：最多$\lceil log_2 k \rceil$次。

image-20220112163021938

最佳归并树

其实也就是多叉哈夫曼树。

参考《考研算法辅导课笔记（七）》———荷马史诗。

由二进制编码扩展到k进制编码。

构造方式：由每次选择最小的2个节点扩展到每次选择最小的k个节点。

如果剩下节点数量不足k个，不足的补0。

节点个数不够如何补0？

注意到，每次我们都是取k个数，但在最后一次取的时候，可能已经不足k个数可取了，所以不妨在算法的开始，我们就先取掉x个数（补上k-x个 0），使得剩下的n-x个数正好能每次取k个取完。

怎么求 x ？

不妨设补上 x 个节点之后就可以构成一棵 k 叉哈夫曼树。

设 k 度节点个数为 t ，叶子节点（已有节点+补上的节点）个数为 m，已有节点个数为 n 。

建立方程：k*t + 1 = 总节点数; m = n + x; t + m = 总节点数

联立解得：(k-1)*t = n-1+x，等价于x = (n-1) % (k-1)。

概念补充：

最佳归并树中将补充的零节点称为虚段。

考试要求计算虚段个数。

坚持原创技术分享，您的支持将鼓励我继续创作！