二分查找
首先,我们抛出一个经典的问题:如何在一个严格递增序列A中找出给定的数x。
最直接的办法就是对序列进行现行扫描所有元素,如果找到x则成功,如果没找到就失败。
这种顺序查找的时间复杂度为O(n),当查询数据较小时,是个很好的选择,但数据量太大就不行了。
由此,我们可以通过二分查找来缩短时间。
一般的二分做法(严格递增递减序列)
明确一点,二分查找是基于有序序列的查找算法,这里仅以严格递增序列为例子,对于其他有序序列做法类似。
二分查找的高效在于每一步二分都能够去除当前区间一半的元素,所以时间复杂度为$O(log n)$。
我们先设[left,right]为序列A的整个下标区间,然后不断二分查找。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include <iostream>
#include <cstdio>
using namespace std;
int binarySearch(int A[],int left,int right,int x){
int mid;
while (left <= right){
mid = (left+right) >> 1;
if(A[mid] == x) return mid;
else if(A[mid] > x) right = mid-1;
else left = mid+1;
}
return -1;
}
int main(){
const int n = 10;
int A[n] = {0,3,5,7,9,11,13,15,16,19};
cout << binarySearch(A,0,n-1,13) << ' ' << binarySearch(A,0,n-1,8) << endl;
return 0;
}
|
这里的循环条件是left <= right,当left>right时可以作为元素x不存在的判定条件。
注意:mid= (left+right)/2中的left+right有可能超出int范围而溢出,所以一般用imd=left + (right-left) >> 1,是等价的。(位运算会稍快一点)
以下所涉及的序列未说明是严格递增递减序列。
对于递增(递减)序列,要在其中找到x(如果有多个)的位置范围。如果我们能够求出序列中第一个大于等于x的元素的位置L,以及序列中第一个大于x的元素的位置R,这样元素x在序列中的存在区间就是[L,R)。
如何求序列中第一个大于等于x的元素的位置(下界)
如果序列中存在元素x,那么序列中第一个大于等于x的元素的位置也就是第一个x的位置,下界;
如果序列中不存在元素x,那么返回值是序列中下标,或者是n。
这里仅以递增序列为例子。
注意:这里的二分区间是[0,n],不再是上面的[0,n-1],因为x可能比序列中所有元素都大。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include <iostream>
#include <cstdio>
using namespace std;
int lower_bound(int A[],int left,int right,int x){
int mid;
while (left < right){
mid = (left+right) >> 1;
if(A[mid] >= x) right = mid;
else left = mid+1;
}
return left;
}
int main(){
const int n = 10;
int A[n] = {0,3,5,7,7,7,7,15,17,19};
cout << lower_bound(A,0,n,7) << ' ' << lower_bound(A,0,n,20) << endl;
return 0;
}
|
说明:
当A[mid]>=x时,说明第一个大于等于x的元素的位置一定在mid处或mid的左侧,所以往[left,mid]查找。
当A[mid]<x时,说明第一个大于等于x的元素的位置一定在mid右侧,所以往[mid+1,right]查找。

配图请细品:)
由于第一个大于等于x的元素的位置肯定存在,所以当left==right时,所夹出来的位置就是所求下标,这里返回right也是一样的。
如何求序列中第一个大于x的元素的位置(上界往上)
做法类似上一个问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include <iostream>
#include <cstdio>
using namespace std;
int upper_bound(int A[],int left,int right,int x){
int mid;
while (left < right){
mid = (left+right) >> 1;
if(A[mid] > x) right = mid;
else left = mid+1;
}
return left;
}
int main(){
const int n = 10;
int A[n] = {0,3,5,7,7,7,7,15,17,19};
cout << lower_bound(A,0,n,7) << ' ' << lower_bound(A,0,n,20) << endl;
return 0;
}
|
眼力好的同学肯定发现了,这里只是把上一问中的A[mid]>=x换成了A[mid]>x,其他完全一样。
说明:
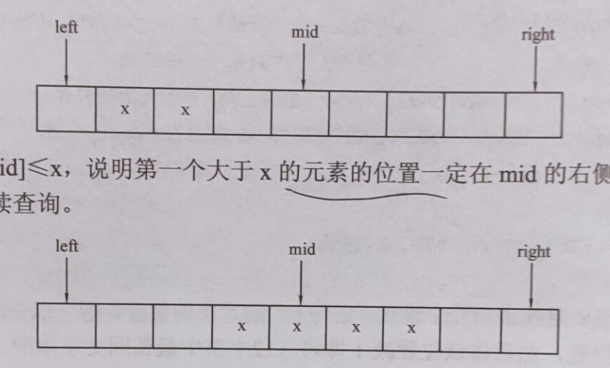
当A[mid]>x时,说明第一个大于x的元素的位置一定在mid处或mid的左侧,所以往[left,right]查找。
当A[mid]<=x时,说明第一个大于x的元素的位置一定在mid的右侧,所以往[mid+1,right]查找。
补充资料
在STL中,C++其实已经帮我们写好了二分的lower_bound和upper_bound函数。
详见:C++语法(九)
如何深入理解二分法以及处理好边界问题:
https://mp.weixin.qq.com/s/3fjDhS3lb5CBrzx6p0XIxw



