蓝桥杯学习总结（十三）

2.6 acwing.1214. 波动数列

第五届蓝桥杯省赛C++A组,第五届蓝桥杯省赛JAVAA组

观察这个数列：
1 3 0 2 -1 1 -2 …
这个数列中后一项总是比前一项增加2或者减少3，且每一项都为整数。
栋栋对这种数列很好奇，他想知道长度为 n 和为 s 而且后一项总是比前一项增加 a 或者减少 b 的整数数列可能有多少种呢？

输入格式
共一行，包含四个整数 n,s,a,b，含义如前面所述。

输出格式
共一行，包含一个整数，表示满足条件的方案数。
由于这个数很大，请输出方案数除以 100000007 的余数。

数据范围
1≤n≤1000,
−10^9≤s≤10^9,
1≤a,b≤10^6
输入样例：
4 10 2 3
输出样例：
2
样例解释
两个满足条件的数列分别是2 4 1 3和7 4 1 -2。

这题很有难度。（连y总都说有难度）

思路：

本质上是个组合问题。

这题组合维度太多，不能用dfs爆搜。

y总配套详细题解：https://www.acwing.com/solution/content/9223/

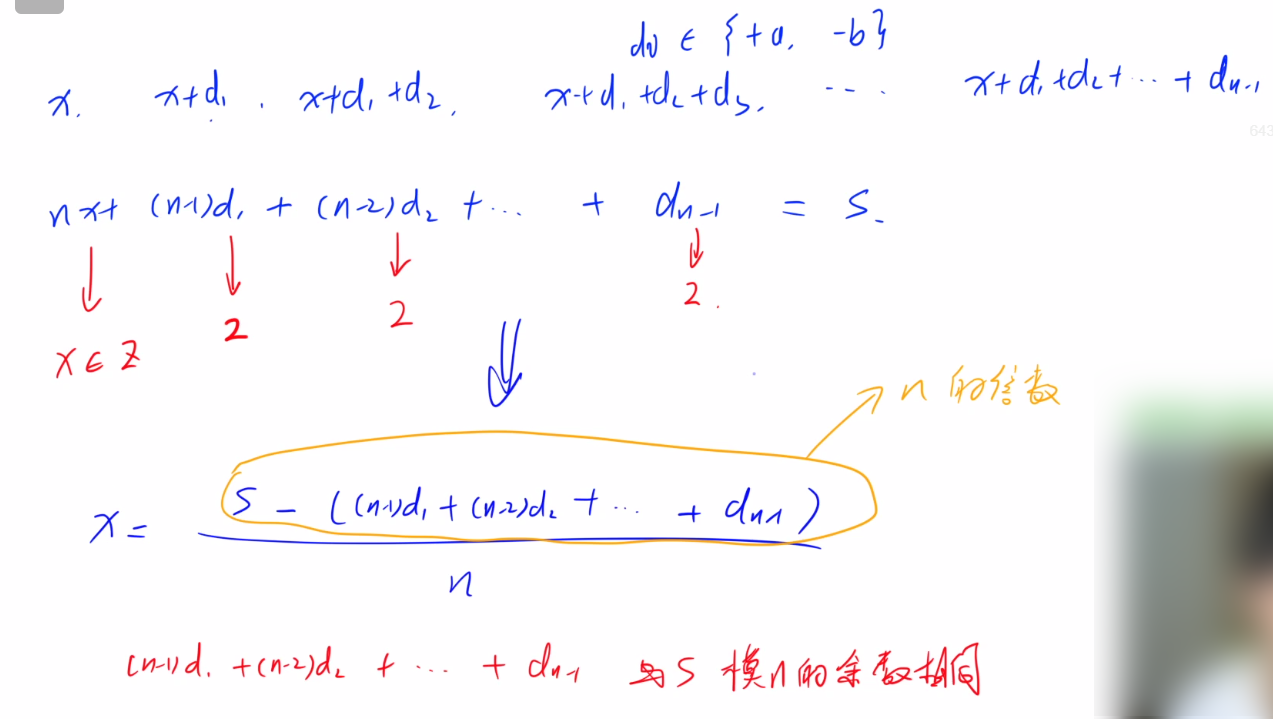
注意：数列的下标更换了，但是意义不变。

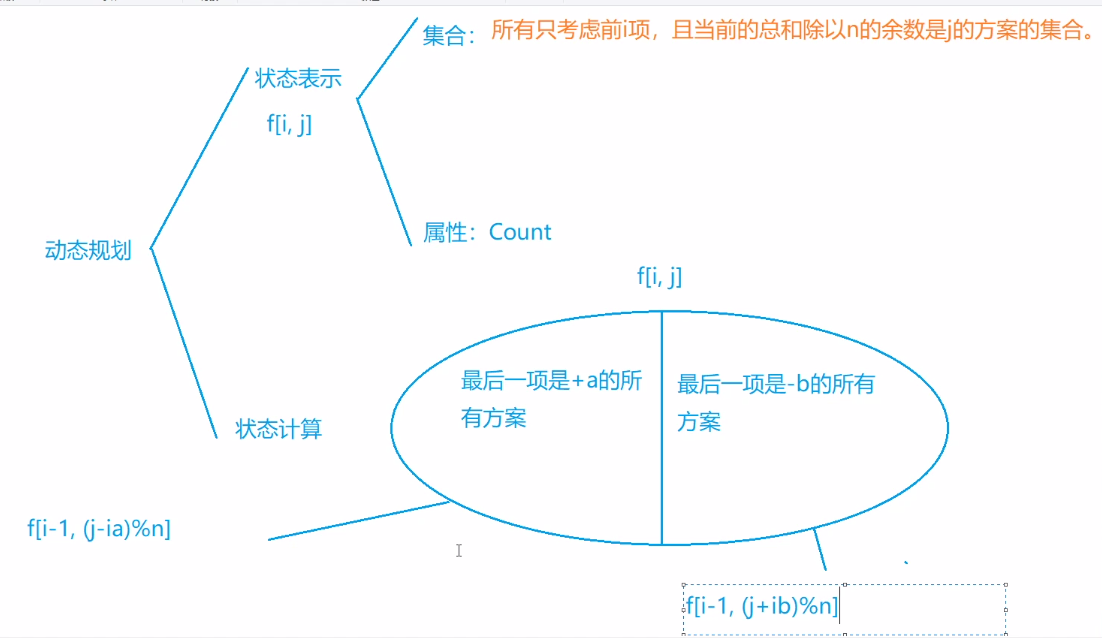
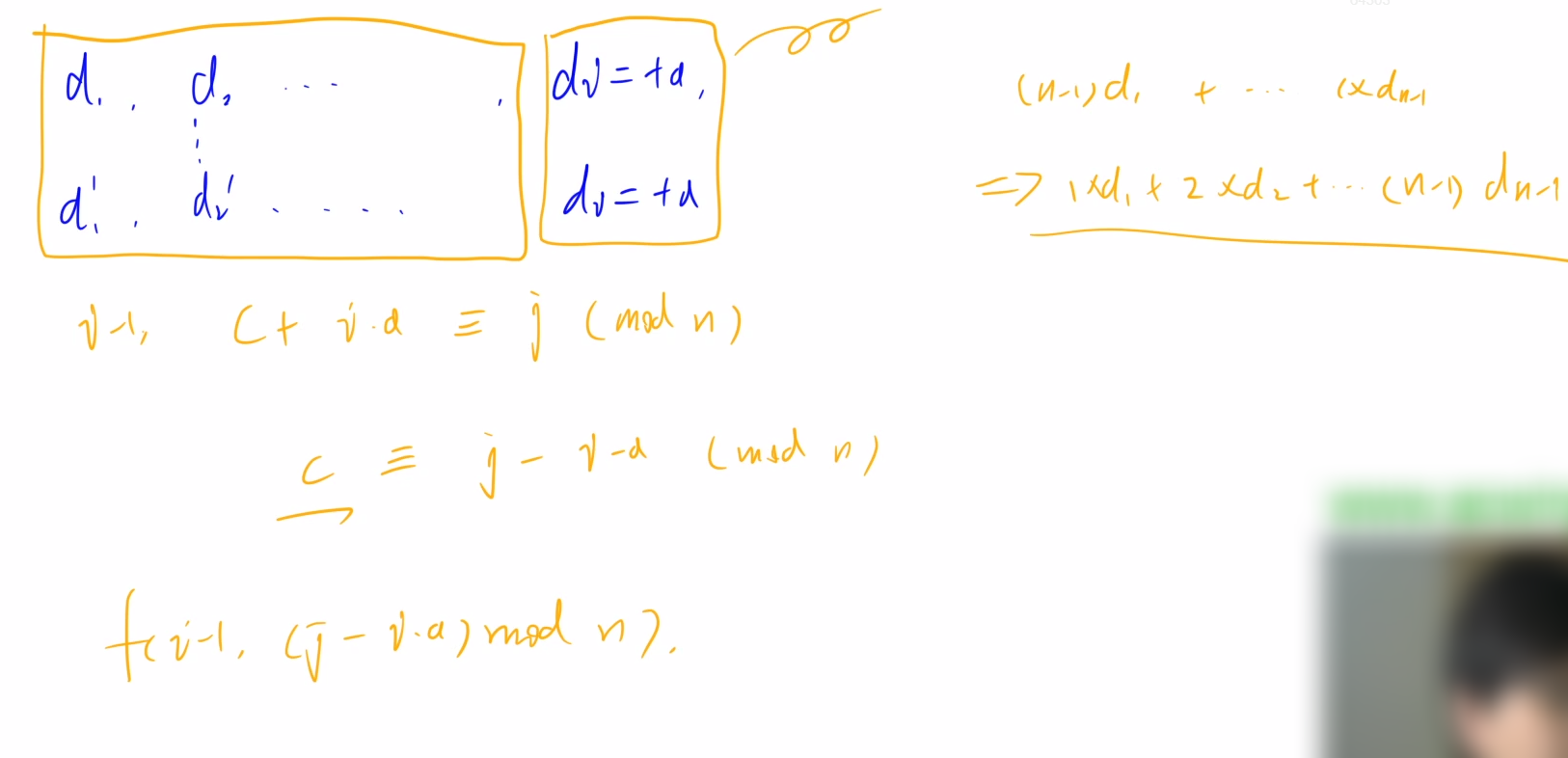
初始化条件：f[0][0]=1。

这题数组第二维不是单调变化的，不能去掉一维。

在数论中，余数都是非负的，例如：-2 % 10 = 8.但是C++中会得到负余数，所以要处理一下。

// y总题解
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 1010,MOD = 100000007;

int f[N][N];
int n,s,a,b;
// 求a mod b的正余数
int get_mod(int a,int b){
    return (a % b + b) % b;
}
int main(){
    cin >> n >> s >> a >> b;

    f[0][0] = 1;
    for (int i = 1;i < n;i++)
        for (int j = 0;j < n;j++){
            //进行求正余数处理，否则会有负数出现，导致计算错误
            f[i][j] = (f[i-1][get_mod(j -i*a,n)] + f[i-1][get_mod(j + i*b,n)]) % MOD;
        }
    // 注意这里要求s mod n的正余数
    // 注意第一位是n-1，不是n
    cout << f[n-1][get_mod(s, n)] << endl;
    return 0;
}

如果不交换数组下标，写成这样也是可行（等价）的。

系数和下标之和为n，所以第i项的的系数为n-i。

所以：f[i][j] = f[i - 1][j - (n - i) * a]

第i个选b：同理：f[i][j] = f[i - 1][j + (n - i) * b]

四 枚举、模拟与排序

1.枚举

1.1 acwing.1210. 连号区间数

第四届蓝桥杯省赛C++B组,第四届蓝桥杯省赛JAVAB组

小明这些天一直在思考这样一个奇怪而有趣的问题：
在 1∼N 的某个排列中有多少个连号区间呢？
这里所说的连号区间的定义是：
如果区间 [L,R] 里的所有元素（即此排列的第 L 个到第 R 个元素）递增排序后能得到一个长度为 R−L+1 的“连续”数列，则称这个区间连号区间。
当 N 很小的时候，小明可以很快地算出答案，但是当 N 变大的时候，问题就不是那么简单了，现在小明需要你的帮助。

输入格式
第一行是一个正整数 N，表示排列的规模。
第二行是 N 个不同的数字 Pi，表示这 N 个数字的某一排列。

输出格式
输出一个整数，表示不同连号区间的数目。

数据范围
1≤N≤10000,
1≤Pi≤N
输入样例1：
4
3 2 4 1
输出样例1：
7
输入样例2：
5
3 4 2 5 1
输出样例2：
9
样例解释
第一个用例中，有 7 个连号区间分别是：[1,1],[1,2],[1,3],[1,4],[2,2],[3,3],[4,4]
第二个用例中，有 9 个连号区间分别是：[1,1],[1,2],[1,3],[1,4],[1,5],[2,2],[3,3],[4,4],[5,5]

思路：

考察数据范围10000，知道时间复杂度大致是O(n*logn)比较合理，实在不行O(n^2)也勉强能行。

先写暴力解法，再优化。

排列说明无重复数字。

”不难“发现，连续区间等价于Max - Min = b - a。因为没有重复数字，刚好填满区间，无空缺。

优化之后，枚举第二重循环同时求最大最小值并判断连续区间。

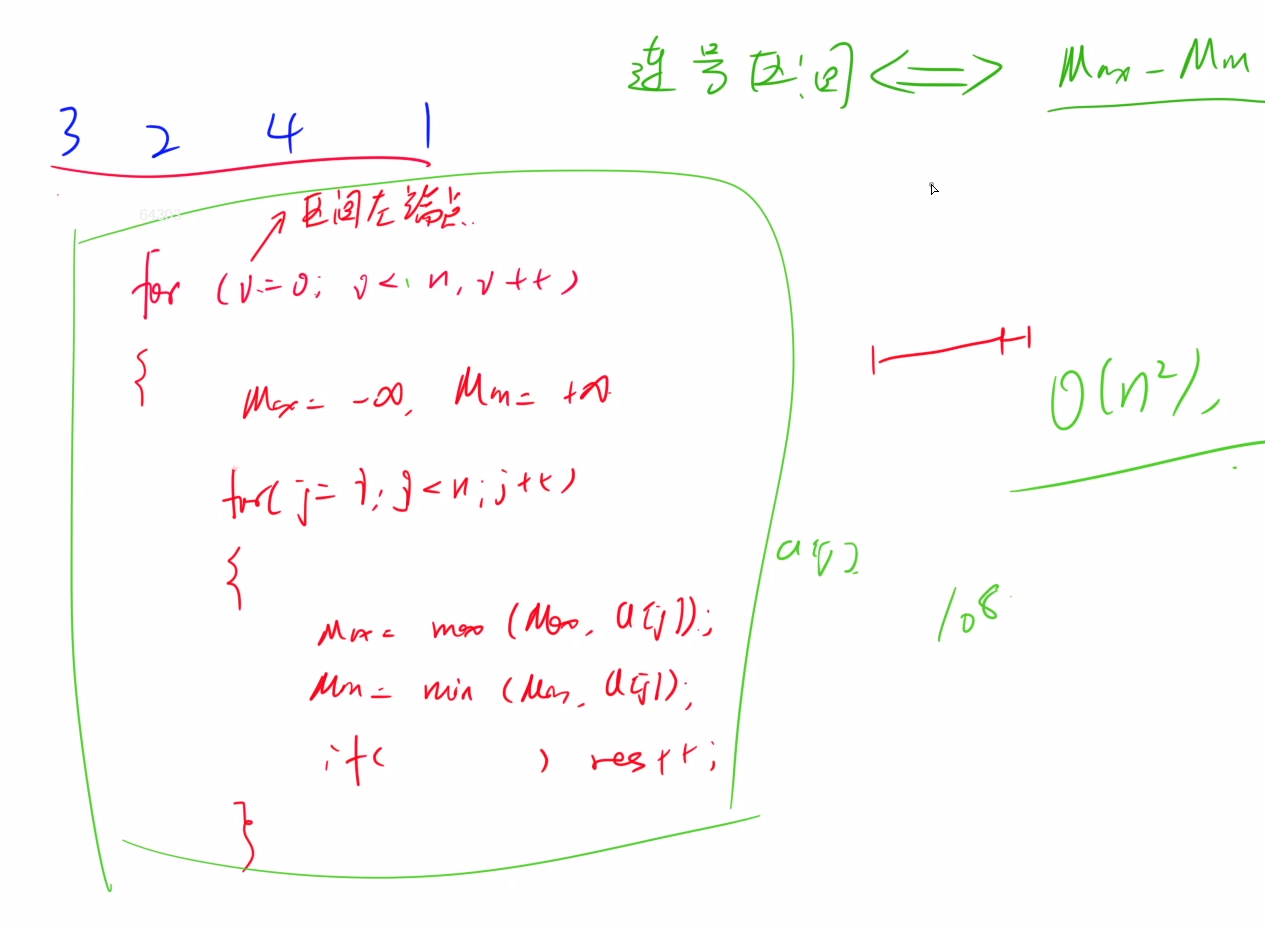
由于代码量比较小，所以执行的指令较少，时间复杂度的常数比较小，是能AC的。

时间复杂度：O(n^2)。

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 10010,INF = 10010;

int n;
int a[N];
int main(){
    cin >> n;
    for (int i  = 0;i < n;i ++) cin >> a[i];

    int res = 0;
    for (int i = 0;i < n;i++){// 枚举区间左端点
        int maxv = -INF,minv = INF;// 注意不要写反了
        for (int j = i;j < n;j ++){// 枚举区间右端点
            maxv  = max(maxv,a[j]);
            minv = min(minv,a[j]);
            if (maxv - minv == j - i) res ++;
        }
    }
    cout << res << endl;
    return 0;
}