grant's Blog

记录生活中的点点滴滴

2022春季每日一题笔记（三）

发表于 更新于 分类于 ，   阅读次数： Valine：
本文字数： 11k 阅读时长 ≈ 10 分钟

第三周

T1—1683. 困牛放牧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Farmer John 的三头获奖奶牛 Bessie、Elsie 和 Mildred，总是会迷路走到农场上遥远的地方去！
他需要你帮助将她们一起赶回来。
农场的草地大体是一块狭长的区域——我们可以将其想象成一条数轴，奶牛可以占据数轴上的任意整数位置。
这 3 头奶牛现在正位于不同的整数位置，Farmer John 想要移动她们，使得她们占据三个相邻的位置（例如，位置 6、7、8）。
不幸的是，奶牛们现在很困，Farmer John 要让她们集中精力听从命令移动并不容易。
任意时刻，他只能使得一头处在“端点”（在所有奶牛中位置最小或最大）位置的奶牛移动。
当他移动奶牛时，他可以命令她走到任意一个未被占用的整数位置，只要在新的位置上她不再是一个端点。
可以看到随着时间的推移，这样的移动可以使奶牛们趋向越来越近。
请求出使得奶牛们集中到相邻位置所进行的移动次数的最小和最大可能值。

输入格式
输入包含一行，包括三个空格分隔的整数，为 Bessie、Elsie 和 Mildred 的位置。

输出格式
输出的第一行包含 Farmer John 需要将奶牛们聚集起来所需进行的最小移动次数。

第二行包含他将奶牛聚集起来能够进行的最大移动次数。

数据范围
每个位置均为一个范围 1…10^9 内的整数。

输入样例：
4 7 9
输出样例：
1
2
样例解释
最小移动次数为 1——如果 Farmer John 将位置 4 的奶牛移动到位置 8，那么奶牛们就处在连续的位置 7、8、9。
最大移动次数为 2。例如，位置 9 的奶牛可以被移动到位置 6，然后位置 7 的奶牛可以被移动到位置 5。

简单的贪心题，可以大概猜出来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
#include <algorithm>
using namespace std;

int main(){
    int a,b,c;
    cin >> a >> b >> c;
    
    // 题目已经排序
    int Min = min(a,min(b,c));
    int Max = max(a,max(b,c));
    b = a+b+c - Min - Max;
    
    if (b-Min == 1 && Max-b == 1){ // 情况1：已经连续
        cout << 0 << '\n' << 0 << '\n';
        return 0;
    }
    // 情况2：未连续
    // 分别求中间两个间隔的最大值和最小值
    int d1 = max(b-Min,Max-b),d2 = min(b-Min,Max-b);
    cout << (d2 == 2 ? 1 : 2) << '\n';
    cout << d1-1 << '\n'; // 最大移动数就是最大间隔-1，可以模拟一下
    
    return 0;
}

T2—1470. 水桶传递队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
农场上起火了，奶牛们正在紧急赶去灭火！
农场可以用一个像这样的 10×10 的字符方阵来描述：
..........
..........
..........
..B.......
..........
.....R....
..........
..........
.....L....
..........
字符’B’表示正着火的牛棚，字符’L’表示一个湖，而字符’R’表示农场上的一块巨大岩石。
奶牛们想要沿着一条湖到牛棚之间的路径组成一条“水桶传递队列”，这样她们就可以沿着这条路径传递水桶来帮助灭火。
当两头奶牛在东南西北四个方向上相邻时水桶可以在她们之间传递。
湖边的奶牛也是如此——奶牛只能在紧挨着湖的时候才能用水桶从湖里取水。
类似地，奶牛只能在紧挨着牛棚的时候才能用水去灭牛棚的火。
请帮助求出奶牛们为了组成这样的“水桶传递队列”需要占据的’.’格子的最小数量。
奶牛不能站在岩石所在的方格之内，此外保证牛棚和湖不是相邻的。

输入格式
输入包含 10 行，每行 10 个字符，描述这个农场的布局。
输入保证图案中恰有一个字符’B’、一个字符’L’以及一个字符’R’。

输出格式
输出一个整数，为组成一条可行的水桶传递队列所需要的奶牛的最小数量。

输入样例：
..........
..........
..........
..B.......
..........
.....R....
..........
..........
.....L....
..........
输出样例：
7
样例解释
在这个例子中，以下是一个可行的方案，使用了最小数量的奶牛（7）：
..........
..........
..........
..B.......
..C.......
..CC.R....
...CCC....
.....C....
.....L....
..........

题解一：标准的BFS模板题。复习一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 12;
char g[N][N];
bool st[N][N];
int dist[N][N],dx[] = {0,0,1,-1},dy[] = {1,-1,0,0};

struct Point{
    int x,y;
}q[N*N];
Point s,ro,ed;

int bfs(Point s){
    int hh = 0,tt = 0;
    q[0] = s;
    st[s.x][s.y] = true;
    memset(dist,-1,sizeof dist);
    dist[s.x][s.y] = 0;
    
    while (hh <= tt){
        auto t = q[hh++];
        int x = t.x,y = t.y;
        
        for (int i = 0;i < 4;i ++){
            int x1 = x + dx[i],y1 = y + dy[i];
            if (x1 < 0 || x1 >= 10 || y1 < 0 || y1 >= 10 || st[x1][y1])
                continue;
            if (dist[x1][y1] != -1) continue;
            if (x1 == ro.x && y1 == ro.y) continue;
            dist[x1][y1] = dist[x][y] + 1;
            st[x1][y1] = true;
            if (x1 == ed.x && y1 == ed.y) return dist[x1][y1];
            q[++tt] = {x1,y1};
        }
    }
    return -1;
}

int main(){
    for (int i = 0;i < 10;i ++)
        for (int j = 0;j < 10;j ++){
            cin >> g[i][j];
            if (g[i][j] == 'L') s = {i,j};
            if (g[i][j] == 'R') ro = {i,j};
            if (g[i][j] == 'B') ed = {i,j};
        }
        
    cout << bfs(s)-1 << '\n';
    return 0;
}

题解二：简单的数学逻辑题。参考自大佬。两个速度差不多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
#include <algorithm>
using namespace std;
char g[11][11];

int main(){
    int lx,ly,rx,ry,bx,by;
    for (int i = 0;i < 10;i ++)
        for (int j = 0;j < 10;j ++){
            cin >> g[i][j]; // 记录湖，石，火的位置
            if (g[i][j] == 'L') lx = i,ly = j;
            if (g[i][j] == 'R') rx = i,ry = j;
            if (g[i][j] == 'B') bx = i,by = j;
        }
        
    int d1 = abs(lx-rx) + abs(ly-ry); // 计算曼哈顿距离
    int d2 = abs(rx-bx) + abs(ry-by);
    int d3 = abs(bx-lx) + abs(by-ly);
    
    if ((lx == bx || ly == by) && d1 + d2 == d3) // 湖火共线且石堵在线上
        cout << d3 + 1 << '\n';
    else cout << d3 - 1 << '\n';
    return 0;    
}

T3—1761. 阻挡广告牌

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
在漫长的产奶期间，奶牛贝茜喜欢透过窗户盯着马路对面的两个巨大的矩形广告牌，上面写着“农夫亚历克斯的惊人开胃苜蓿”和“农夫格雷格的大粒谷物”。
广告牌上这两种精美的牛饲料看上去比农场里的草美味的多。
有一天，当贝茜凝视着窗外时，她惊异地看到一辆巨大的矩形卡车停在马路对面。
卡车的侧面有一个广告，上面写着“农夫史密斯的精湛牛排”。
贝茜对此不太感兴趣，但她非常担心卡车可能会阻挡她观看最喜欢的两个广告牌的视野。
给定两个广告牌的位置和卡车的位置，请计算两个广告牌的仍然可见的总面积。
卡车可能挡到两个广告牌或只挡到其中一个，或都挡不到。

输入格式
第一行包含四个整数 x1,y1,x2,y2，其中 (x1,y1) 和 (x2,y2) 表示在贝茜的二维视野中，第一个广告牌的左下角和右上角坐标。
第二行按照如上形式，包含四个整数，表示第二个广告牌的左下角和右上角坐标。
第三行按照如上形式，包含四个整数，表示卡车侧面的左下角和右上角坐标。

输出格式
输出两个广告牌的仍然可见的总面积。

数据范围
−1000≤x1,y1,x2,y2≤1000,
保证两个广告牌之间重叠面积为 0。

输入样例：
1 2 3 5
6 0 10 4
2 1 8 3
输出样例：
17
样例解释
第一块广告牌的可见面积为 5，第二块广告牌的可见面积为 12。

考察计算几何。

求矩形交集。两个矩形的交集一定是一个矩形。

可以这样做：

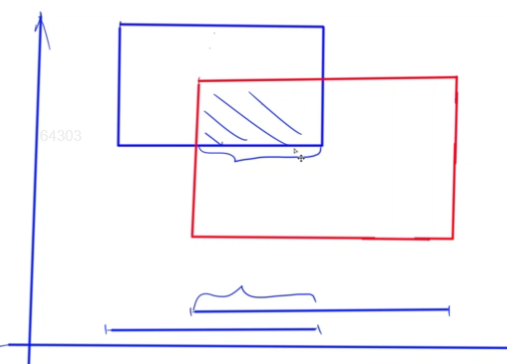
image-20220330210547770

先求两个矩形的横轴区间的重叠部分，再求它们的纵轴区间的重叠部分，乘起来就是交集的面积。

需要用到两个线段求交集的公式：

image-20220330211015376

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
#include <algorithm>
using namespace std;
int a[3][4];
// 求两线段a-b,c-d的重叠部分长度
int seg_union(int a,int b,int c,int d){return max(0,min(b,d) - max(a,c));}

int area(int i){return (a[i][2] - a[i][0]) * (a[i][3] - a[i][1]);}

int main(){
    for (int i = 0;i < 3;i ++)
        for (int j = 0;j < 4;j ++)
            cin >> a[i][j];
    
    int cnt = 0;
    for (int i = 0;i < 2;i ++){
        cnt += seg_union(a[i][0],a[i][2],a[2][0],a[2][2])
        * seg_union(a[i][1],a[i][3],a[2][1],a[2][3]);
    }
    
    cout << area(0) + area(1) - cnt << '\n';
    return 0;
}

T4—1749. 阻挡广告牌 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
奶牛贝茜曾经从农场中向外看去，可以看到两个刊登着美味的牛饲料广告的广告牌，这令她非常满意。
不幸的是，其中一个广告牌最近已更新，现在刊登着广告“农民拉里的割草机”。
但是贝茜可不喜欢割草机，这些割草机只会把她爱吃的草割的一干二净。
幸运的是，剩下的牛饲料广告牌位于割草机广告牌的前面，有可能将其遮挡住。
贝茜希望这个讨厌的割草机广告牌能够完全从自己的视线中消失，并为此制定了一个冒险计划。
她计划从谷仓里偷一个大的矩形防水布，并在深夜偷偷溜走，用它覆盖割草机广告牌的其余部分，使得她能完全看不到割草机广告牌。
给定两个广告牌的位置，请帮助贝茜计算她所需要的防水布的最小面积。
由于谷仓中只有矩形的防水布，因此贝茜发现为了将割草机广告牌完全遮盖，所需的防水布面积可能会大于割草机广告牌的裸露面积，如下例所示。
防水布在放置时，其边必须与广告牌的边平行，即不能倾斜放置。

输入格式
第一行包含四个整数 x1,y1,x2,y2，其中 (x1,y1) 和 (x2,y2) 表示割草机广告牌的左下角和右上角坐标。
第二行按照如上形式，包含四个整数，表示牛饲料广告牌的左下角和右上角坐标。
牛饲料广告牌可能完全遮盖了割草机广告牌，或部分遮盖了割草机广告牌，也可能完全没有遮盖割草机广告牌。

输出格式
输出用来遮盖割草机广告牌的防水布的最小面积。

数据范围
−1000≤x1,y1,x2,y2≤1000
输入样例：
2 1 7 4
5 -1 10 3
输出样例：
15
样例解释
虽然牛饲料广告牌遮盖住了割草机广告牌的右下角的一部分，但这并没有起到作用。
想要完全遮盖割草机广告牌，仍然需要一块和它尺寸相同的防水布。

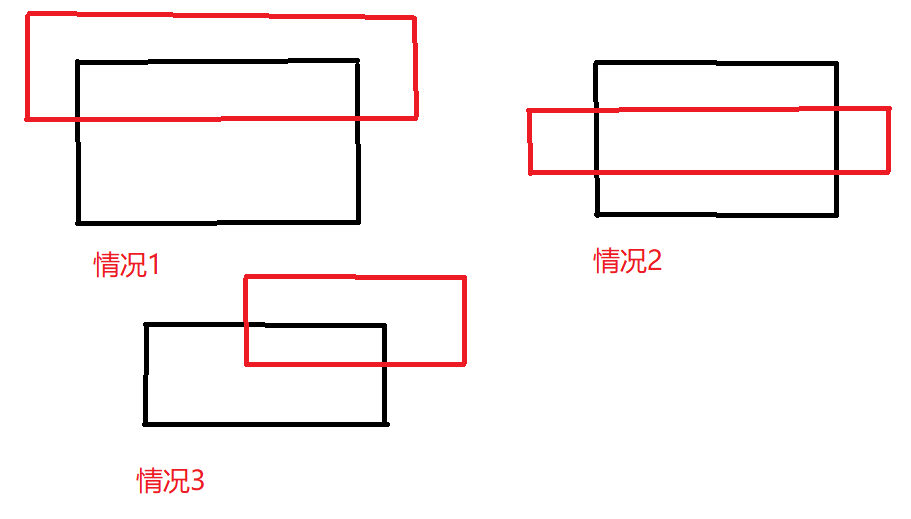
分类讨论一下。

第一种情况，牛饲料广告的横向边完全覆盖割草机的横向边而且牛饲料的纵向边不能被割草机完全覆盖，纵向边是完全对称的，这种情况防水布的面积就是重叠部分的面积；

其余两种情况，防水布的面积就是割草机的面积。

image-20220331193115471

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
#include <algorithm>
using namespace std;
int x[2][2],y[2][2];

int seg_union(int a,int b,int c,int d){return max(0,min(b,d) - max(a,c));}

int area(int i){return (x[i][1] - x[i][0])*(y[i][1] - y[i][0]);}

bool check(int a,int b,int c,int d){return a < c && b > d;}

int main(){
    for (int i = 0;i < 2;i ++)
        cin >> x[i][0] >> y[i][0] >> x[i][1] >> y[i][1];

    int a = seg_union(x[0][0],x[0][1],x[1][0],x[1][1]);
    int b = seg_union(y[0][0],y[0][1],y[1][0],y[1][1]);
    if (a == x[0][1] - x[0][0] && !check(y[0][0],y[0][1],y[1][0],y[1][1]))
        cout << area(0) - a*b << '\n';
    else if (b == y[0][1] - y[0][0] && !check(x[0][0],x[0][1],x[1][0],x[1][1]))
        cout << area(0) - a*b << '\n';
    else cout << area(0) << '\n';
    return 0;
}

T5—1737. 传送

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Farmer John 最讨厌的农活是运输牛粪。
为了精简这个过程，他制造了一个伟大的发明：便便传送门！
与使用拖拉机拖着装满牛粪的大车从一个地点到另一个地点相比，他可以使用便便传送门将牛粪从一个地点瞬间传送到另一个地点。
Farmer John 的农场沿着一条长直道路而建，所以他农场上的每个地点都可以简单地用该地点在道路上的位置来表示（相当于数轴上的一个点）。
一个传送门可以用两个数 x 和 y 表示，被拖到地点 x 的牛粪可以瞬间传送到地点 y，反之亦然。
Farmer John 想要将牛粪从地点 a 运输到地点 b，他建造了一个可能对这一过程有所帮助的传送门（当然，如果没有帮助，他也可以不用）。
请帮助他求出他需要使用拖拉机运输牛粪的总距离的最小值。

输入格式
输入仅包含一行，为四个用空格分隔的整数：a 和 b，表示起始地点和结束地点，后面是 x 和 y，表示传送门。
所有的位置都是范围为 0…100 的整数，不一定各不相同。

输出格式
输出一个整数，为 Farmer John 需要用拖拉机运输牛粪的最小距离。

输入样例：
3 10 8 2
输出样例：
3
样例解释
在这个样例中，最佳策略是将牛粪从位置 3 运到位置 2，传送到位置 8，再运到位置 10。
所以需要用拖拉机的总距离为 1+2=3。

水题，分类讨论。

1
2
3
4
5
6
7
8
9
10
11
#include <iostream>
#include <algorithm>
using namespace std;

int main(){
    int a,b,x,y;
    cin >> a >> b >> x >> y;
    // 1.a直接送到b，2.a经过x到y再送到b，3.a经过y到x再送到b
    cout << min(min(abs(b-a),abs(a-x) + abs(b-y)),abs(a-y) + abs(b-x)) << '\n';
    return 0;
}

T6—1725. 组队井字游戏

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Farmer John 有 26 头奶牛，恰好她们名字都以不同的字母开头，所以 Farmer John 用每头奶牛的名字的首字母来指代她——一个 A…Z 之间的字母。
这些奶牛最近沉迷于井字游戏，但是由于她们并不满足只有两头奶牛可以一起玩，她们改编了这个游戏，可以让许多奶牛可以一块儿玩！
就像常规的井字游戏一样，这个游戏是在一块 3×3 的棋盘上进行的，只是与仅用 X 和 O 不同，每个格子用一个 A…Z 之间的字母标记，表示占有这个格子的奶牛名字的首字母。
以下是一个棋盘的例子：
COW
XXO
ABC
这些奶牛会在她们迷惑于如何判断胜负之前就占满这九个格子。
显然，就像常规的井字游戏一样，如果任何一头奶牛占有了一整行、一整列，或是一整条对角线，那么这头奶牛就获胜了。
然而，由于奶牛认为多牛游戏中这并不容易出现，所以她们决定允许奶牛组成两牛一队，如果某一行、一列，或是一条对角线仅包含一队的两头奶牛的字母，并且同时包含了这两头奶牛（不仅仅是一头）的字母，那么这一队就获胜。
请帮助奶牛们判断有多少头奶牛或是两头奶牛组成的队伍可以获胜。
注意棋盘上的同一个格子可能在不同奶牛或队伍的获胜中均被用到。

输入格式
输入包含三行，每行三个 A…Z 之间的字符。

输出格式
输出包含两行。
第一行，输出能够获胜的单独的奶牛的数量。
第二行，输出能够获胜的两头奶牛组成的队伍的数量。

输入样例：
COW
XXO
ABC
输出样例：
0
2
样例解释
在这个例子中，没有单独的奶牛可以获得胜利。
但是，如果奶牛 C 和奶牛 X 组队，她们可以通过 C−X−C 对角线获胜。
同样地，如果奶牛 X 和 O 组队，她们可以通过中间一行取胜。

我的写法比较麻烦。手动去重。

注意：C++中的unordered_map和unordered_set不能直接以pair作为键名。

对于pair和自定义的结构需要作为键的话，需要自己实现哈希函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
typedef pair<int,int> PII;
char g[3][3];
vector<vector<int> > v;

int main(){
    for (int i = 0;i < 3;i ++)
        for (int j = 0;j < 3;j ++)
            cin >> g[i][j];
    // 处理行    
    for (int i = 0;i < 3;i ++){
        vector<int> t;
        t.push_back(g[i][0]);
        if (g[i][1] != g[i][0]) t.push_back(g[i][1]);
        if (g[i][2] != g[i][0] && g[i][2] != g[i][1]) t.push_back(g[i][2]);
        v.push_back(t);
    }
    // 处理列
    for (int i = 0;i < 3;i ++){
        vector<int> t;
        t.push_back(g[0][i]);
        if (g[1][i] != g[0][i]) t.push_back(g[1][i]);
        if (g[2][i] != g[0][i] && g[2][i] != g[1][i]) t.push_back(g[2][i]);
        v.push_back(t);
    }
    // 处理主对角线
    vector<int> t1;
    t1.push_back(g[0][0]);
        if (g[1][1] != g[0][0]) t1.push_back(g[1][1]);
        if (g[2][2] != g[0][0] && g[2][2] != g[1][1]) t1.push_back(g[2][2]);
        v.push_back(t1);
    // 处理反对角线    
    vector<int> t2;
    t2.push_back(g[0][2]);
        if (g[1][1] != g[0][2]) t2.push_back(g[1][1]);
        if (g[2][0] != g[0][2] && g[2][0] != g[1][1]) t2.push_back(g[2][0]);
        v.push_back(t2);
    
    set<int> set1;
    set<PII> set2;
    for (vector<int> t : v){
        if (t.size() == 1) set1.insert(t[0]);
        if (t.size() == 2){
            if (t[0] > t[1]) swap(t[0],t[1]); // 注意这里，否则{x,y}和{y,x}会被认为不同
            set2.insert({t[0],t[1]});
        }
    }
    cout << set1.size() << '\n' << set2.size() << '\n';
    return 0;
}

简便写法，y总。用set去重，不用手动去重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <string>
#include <set>
#include <vector>
#include <algorithm>
using namespace std;
string g[3];
set<set<char> > ans[2];

void insert(vector<vector<int> > p){
    set<char> s;
    for (auto &it : p){
        s.insert(g[it[0]][it[1]]);
    }
    
    if (s.size() == 1) ans[0].insert(s);
    else if (s.size() == 2) ans[1].insert(s);
}

int main(){
    for (int i = 0;i < 3;i ++) cin >> g[i];
    
    for (int i = 0;i < 3;i ++) insert({{i,0},{i,1},{i,2}});
    
    for (int i = 0;i < 3;i ++) insert({{0,i},{1,i},{2,i}});
    
    insert({{0,0},{1,1},{2,2}});
    
    insert({{0,2},{1,1},{2,0}});
    
    cout << ans[0].size() << '\n' << ans[1].size() << '\n';
    return 0;
}
坚持原创技术分享，您的支持将鼓励我继续创作！