grant's Blog

记录生活中的点点滴滴

蓝桥杯学习总结（三九）

发表于 更新于 分类于 ，   阅读次数： Valine：
本文字数： 7.3k 阅读时长 ≈ 7 分钟

3 acwing.1213. 斐波那契

第五届蓝桥杯省赛C++A组,第五届蓝桥杯省赛JAVAA组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
斐波那契数列大家都非常熟悉。它的定义是：
f(x)=1....(x=1,2)
f(x)=f(x−1)+f(x−2)....(x>2)
对于给定的整数 n 和 m，我们希望求出：
f(1)+f(2)+…+f(n) 的值。
但这个值可能非常大，所以我们把它对 f(m) 取模。
但这个数字依然很大，所以需要再对 p 求模。

输入格式
输入包含多组数据。
每组数据占一行，包含三个整数 n,m,p。

输出格式
每组数据输出一个整数，表示答案。
每个数占一行。

数据范围
0<n,m,p<10^18
测试数据不超过100组

输入样例1：
2 3 5
输出样例1：
0
输入样例2：
15 11 29
输出样例2：
25

思路：

参考题解：https://www.acwing.com/solution/content/43729/

y总说了，这题巨难，做好心理准备。（看着寥寥无几的题解和通过数就知道了）

应该是我目前为止遇到最难的题了。（蓝桥杯不简单）

难点：数据范围特大，需要取2次模，多组测试数据。（斐波那契数列可能没你想的那么简单！）

题目涉及到斐波那契求前n项和，可以参考 acwing.1303. 斐波那契前 n 项和。（矩阵快速幂）

前n项和Sn和第m项f(m)都可能会非常大，先考虑Sn % f(m)有没有公式表示，因为它不可能直接存下来，再考虑它mod p，p相比前面的就小得多。

之前介绍了矩阵快速幂求解前n项和，这里直接推导数学公式计算。（斐波那契前 n 项和公式）

image-20210705132018482

所以：Sn = f(n+2) - 1。

image-20210706115427262

image-20210706115509499

image-20210706115530101

image-20210706111228721

矩阵快速幂求Fibonacci数列第n项就不再介绍了，具体参见蓝桥杯（三七）。

注意到数据范围是10^18，大概是2^60，计算a=a*a时用到两个10^18相乘就是10^36，超过long long的范围，所以需要高精度或者龟速乘来处理。

龟速乘（慢工出细活，时间换精度），原理类似快速幂，将乘法转化成加法来处理爆long long的问题，相应的时间也会从O(1)变成O(logn)。

a(10)*b(10) = a(10)*b(2)，eg. a(10)*19(10) = a(10)*10011(2) = 2^0 *a +2^1 *a +2^4 *a

快速幂和龟速乘都用到了倍增思想以及二进制。

注：上面图片中推导过程不太完整，有部分地方没有说明，但是在代码中会完整计算，样例也会基本覆盖所有情况。（再次吐槽，这题真的超级麻烦）

参考：https://www.acwing.com/blog/content/4794/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 龟速乘与快速幂的对比
//龟速乘,利于快速幂的思想进行乘 
ll mul(ll n,ll m,ll p){// 相乘爆long long，相加不会爆long long
    ll res = 0;
    while(m){
        if(m%2 == 1){
            res = (res + n)%p;
        }
        n = n*2%p;
        m /= 2;
    } 
    return res;
}
//快速幂
ll power(ll n,ll m,ll p){
    ll ans = 1;
    while(m != 0){
        if(m % 2 == 1)
            ans = ans * n % p;
        n = n * n % p;
        m = m/2;
    }
    return ans;
}

代码：

注意：long long的输入输出很容易出错，导致整道题错误！！！

mod p与% p的区别：前者是数学上的取模运算，结果>=0且<p；后者是C++中的取模运算，结果可能为负数，需要转化为正数。

代码量和注释量都非常大！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long LL;

LL n,m,p;
LL qmul(LL a,LL b){// 龟速乘计算(a*b) % p
    LL res = 0;
    while (b){
        if (b & 1) res = (res + a) % p;// b(2)的末位是1
        a = (a + a) % p;
        b >>= 1;// b(2)向右移动一位
    }
    return res;
}

void mul(LL c[][2],LL a[][2],LL b[][2]){// 可以省略第1维，后面不能省略
    LL temp[2][2] = {0};

    for (int i = 0;i < 2;i++)
        for (int j = 0;j < 2;j++)
            for (int k = 0;k < 2;k++)
                temp[i][j] = (temp[i][j] + qmul(a[i][k],b[k][j])) % p;// 龟速乘替代普通乘

    memcpy(c,temp,sizeof temp);// sizeof c是错误的
}

LL F(LL n){// Fn = F1*a^(n-1)
    if (!n) return 0;// 特判n=0的情况，否则陷入死循环
    
    LL f[2][2] = {1,1};// 初始矩阵F1 = [1 1;0 0]，第1行是f(1),f(2)
    LL a[2][2] = {0,1,1,1};// 等价于{{0,1},{1,1}}

    for(LL k = n-1; k ;k >>= 1){// 等价于n--;while(n){...k >>= 1}
        if (k & 1) mul(f,f,a);
        mul(a,a,a);
    }
    return f[0][0];
}

LL H(LL m,LL k){// 计算(f(m-1)*f(k) - 1)  (mod f(m))，利用Fibonacci两数相乘结论
    // 参考最后一种情况
    if (k % 2)// k是奇数，结果是f(m-k)-1  (mod f(m))，m = k不可能出现，不用特判
    {
        return F(m-k) - 1;
    }
    else// k是偶数，结果是f(m)-f(m-k)-1，f(m)=f(m-k)可能成立，需要特判
    {
        if (k == 0 || (m == 2 && k == 1)) return F(m) - 1;
        else return F(m) - F(m-k) - 1;
    }
}

LL G(LL n,LL m){// 计算(f(n)-1) mod f(m) = (f(n) mod f(m) - 1) mod f(m)
    // 根据n/m，n%m，n/(2m)三个数进行分类讨论，注意是下取整，结果可能出现负数需要特判
    if (m % 2 == 0)// m是偶数
    {
        if (n / m % 2 == 0)// 且n/m是偶数，结果是f(n mod m)-1  (mod f(m))
        {   // 特判n整除m的情况,设n = k*m,利用情况1所归纳出的公式可知f(k*m)=f((k-1)*m)*f(m-1)=...=f(m)*xxx
            // 所以此时f(n) mod f(m) = 0
            if (n % m == 0) return F(m)-1;// F(n % m) = 0，但取模结果为正，所以加上F(m)
            else return F(n % m) - 1;             
        }
        else// 且n/m是奇数，结果是f(m-1)*f(n mod m)  (mod(f(m))
        {
            return H(m,n % m);
        }
    }
    else// m是奇数
    {
        if (n / m % 2 == 0 && n / m / 2 % 2 == 0)// 且n/m和n/(2m)都是偶数，结果是f(n mod m)-1  (mod f(m))
        {
            if (n % m == 0) return F(m)-1;// F(n % m) = 0，但取模结果为正，所以加上F(m)
            else return F(n % m) - 1; 
        }
        else if (n / m % 2 == 0 && n / m / 2 % 2)// 且n/m是偶数，n/(2m)是奇数，结果是f(m)-f(n mod m)-1  (mod f(m))
        {
            // 特判f(m) = f(n mod m)的情况，只可能是f(1) = f(2)
            if (n % m == 1 && m == 2) return F(m)-1;
            else return F(m) - F(n % m) - 1;
        }
        else if (n / m % 2 && n / m / 2 % 2 == 0)// 且n/m是奇数，n/(2m)是偶数，结果是f(m-1)*f(n mod m)-1  (mod(f(m))
        {
            return H(m,n % m);
        }
        else// 且n/m是奇数，n/(2m)是奇数，结果是f(m)-[f(m-1]*f(n mod m)  (mod(f(m))]-1  (mod(f(m))
        {
            // 当n mod m 是奇数时，套用结论，f(m-1)*f(n mod m) = f(m- n mod m)
            if (n % m % 2)
            {
                // 特判f(m) = f(m- n mod m)的情况，只可能是f(1) = f(2)
                if (m == 2 && m - n % m == 1) return F(m) - 1;
                else return F(m) - F(m - n % m) - 1;
            }
            else// 当n mod m 是偶数时，套用结论，f(m-1)*f(n mod m) = f(m) - f(m- n mod m)
            {
                // 结果是f(m - n mod m)-1  (mod(f(m))，f(m - n mod m)不可能=0，不用特判
                return F(m - n % m) - 1;
            }
        }
    }
}

int main(){
    while(scanf("%lld%lld%lld",&n,&m,&p) != EOF){
        printf("%lld\n",(G(n+2,m) % p + p) % p);// 最终输出的答案应该是：(f(n+2)-1) mod f(m) mod p
    }
    return 0;
}

注意： >> 1 和/ 2不总是等价的，比如-1 >> 1 = -1, -1 / 2 = 0。如果不在F(n)中加入n=0的特判，就会陷入死循环！

4 acwing.1206. 剪格子

第四届蓝桥杯省赛C++A/C组,第四届蓝桥杯省赛JAVAA/C组

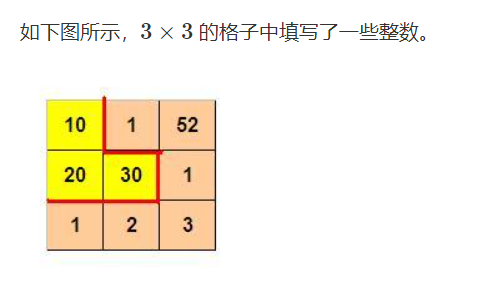
image-20210706181114316

我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是 60。

本题的要求就是请你编程判定：对给定的 m×n 的格子中的整数，是否可以分割为两个连通的部分，使得这两个区域的数字和相等。

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。

如果无法分割，则输出 0。

image-20210706181154353

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
输入格式
第一行包含两个整数 m,n,表示表格的宽度和高度。
接下来是 n 行，每行 m 个正整数，用空格分开。

输出格式
在所有解中，包含左上角的分割区可能包含的最小的格子数目。
如果无法分割，则输出 0。

数据范围
1≤n,m<10,
格子内的数均在1到10000之间。

输入样例1：
3 3
10 1 52
20 30 1
1 2 3
输出样例1：
3
输入样例2：
4 3
1 1 1 1
1 30 80 2
1 1 1 100
输出样例2：
10

思路：

坑：n和m是反过来的，n行在后面。

这题难度与斐波那契不相上下。（高难预警）

错误预警：

  1. 没有判断剪开后只有两个连通块；
  2. 按照一笔能画完的方式搜索；
  3. 按照两笔能画完的方式搜索。

以上都是错误的！

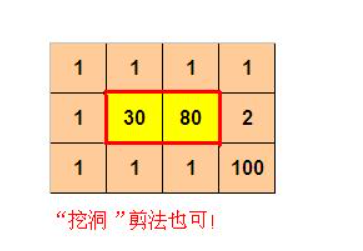
蓝桥杯官网仅包含了以左上角为起点，可不重复一笔画完成的裁剪数据，比如题目描述中的图一。

所以说，网上题解水太深，质量参差不齐，你把握不住，还是y总最靠谱！

且看y总的“锯齿状”搜索！

未完待更。

5 acwing.523. 组合数问题

NOIP2016提高组

image-20210706222159450

1
2
3
4
5
6
7
8
9
10
11
12
13
14
输入格式
第一行有两个整数 t, k ，其中 t 代表该测试点总共有多少组测试数据，k 的意义见问题描述。
接下来 t 行每行两个整数 n, m，其中 n, m 的意义见问题描述。

输出格式
共 t 行，每行一个整数代表所有的 0 ≤ i ≤ n, 0 ≤ j ≤ min(i, m) 有多少对 (i, j) 满足 Cji 是 k 的倍数。

数据范围
1≤n,m≤2000,2≤k≤21,1≤t≤10^4
输入样例：
1 2
3 3
输出样例：
1

思路：

前置知识：（排列组合忘完了）

参考排列组合相关知识：https://oi-wiki.org/math/combination/

排列的计算公式如下：

组合数计算公式：

如何理解上述公式? 我们考虑 $n$ 个人 $m(m \leq n)$ 个出来，不排队， 不在乎顺序 $C_{n}^{m}$ 。如果在乎排列那么就是 $A_{n}^{m}$, 如果不在乎那么就要除掉重复，那么重复了多少? 同样选出的来的 $m$ 个人， 他们还要”全排”得 $A_{n}^{m}$, 所以得：

参考题解：https://www.acwing.com/solution/content/3157/

根据题意，划定的组合数的i、j的范围限制在蓝色阴影梯形。我们不妨将区域扩展为n*m的整个矩形，在对角线之上的${C}_{i}^{j}$是不合法的，设为0；对于蓝色阴影梯形，如果$C_i^j\ \%\ k = 0$，设为1，否则设为0。所以整个矩形上的每个点都有一个值，0或1。

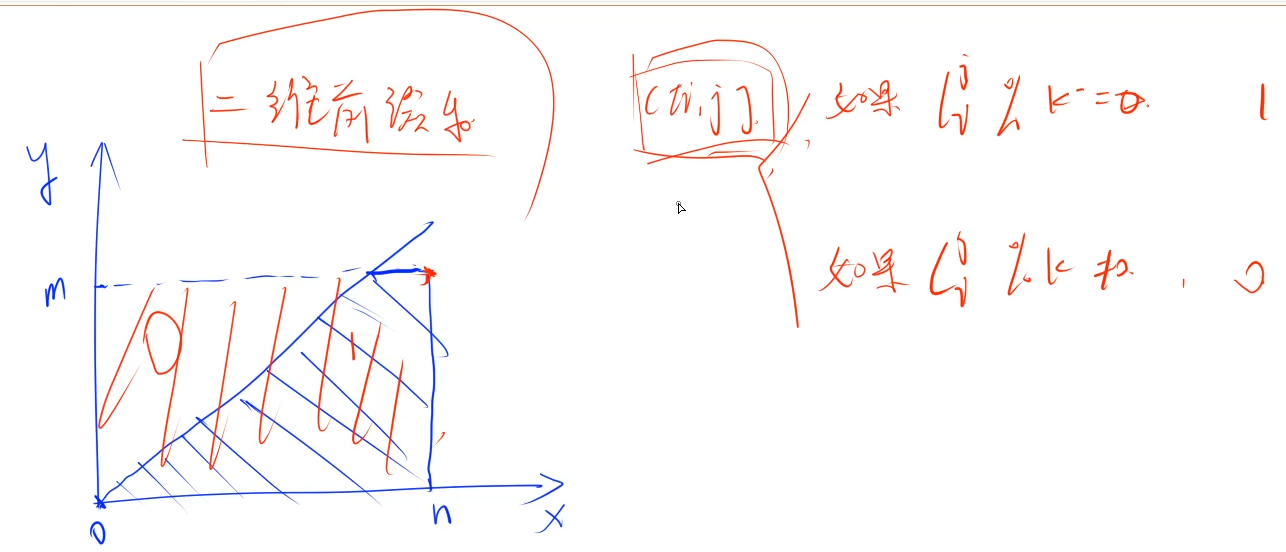
image-20210707171919463

我们再通过二维前缀和来预处理这个矩形区域，计算1的个数，也就是答案。

接下来的问题是如何计算组合数？

  1. 通过题目中给出的定义公式，有阶乘的乘法和除法，很容易爆long long，精度可能也不高，比较麻烦。
  2. 按照递推公式（杨辉三角的公式表达）计算，${C}_{n}^{m}={C}_{n-1}^{m}+{C}_{n-1}^{m-1}$。（时间复杂度：$O(n^2)$）

由于${C}_{n}^{m}$表示从n个不同的数中选择m个数的方案数，因此转化为以下两项之和：一，不选最后一个数，从前n-1个数中选m个数；二，选最后一个数，从前n-1个数中选m-1个数。（参考：算法笔记）

注意：${C}_{n}^{0}={C}_{n}^{n}=1,{C}_{0}^{0}一般约定为1$。

在计算组合数的过程中还需要判断% k的值。

递推出$C_n^m$的时间复杂度是 $O(n^2)$，预处理二维前缀和的时间复杂度也是$O(n^2)$。每次查询时直接查表即可，时间复杂度是 O(1)，一共有 t 次询问，因此总时间复杂度是 $O(n^2+t)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 2010;
int c[N][N];// 组合数 % k的余数
int s[N][N];// 二维前缀和

int main(){
    int t,k;
    scanf("%d%d",&t,&k);

    for (int i = 0;i < N;i++)// 预处理组合数 % k
        for (int j = 0;j <= i;j++){
            if (!j) c[i][j] = 1 % k;
            else c[i][j] = (c[i-1][j-1] + c[i-1][j]) % k;// % k结果为0答案+1，否则不变
            if (!c[i][j]) s[i][j] = 1;// 1，初始化前缀和数组
        }
    // 下标从1开始，方便和c数组统一处理，但需要判断下标是否越界
    for (int i = 0;i < N;i++)// 计算二维前缀和
        for (int j = 0;j < N;j++){
            //s[i][j] = (j <= i && c[i][j] == 0 ? 1 : 0);// 等价于1的处理
            if (i) s[i][j] += s[i-1][j];// 等价于i-1>=0
            if (j) s[i][j] += s[i][j-1];
            if (i && j) s[i][j] -= s[i-1][j-1];
        }

    // 处理询问
    int n,m;
    while (t--){
        scanf("%d%d",&n,&m);
        printf("%d\n",s[n][m]);
    }
    return 0;
}
坚持原创技术分享，您的支持将鼓励我继续创作！