蓝桥杯学习总结（四十）

6 acwing.1171. 距离

《信息学奥赛一本通》

给出 n 个点的一棵树，多次询问两点之间的最短距离。
注意：
边是无向的。
所有节点的编号是 1,2,…,n。
    
输入格式
第一行为两个整数 n 和 m。n 表示点数，m 表示询问次数；
下来 n−1 行，每行三个整数 x,y,k，表示点 x 和点 y 之间存在一条边长度为 k；
再接下来 m 行，每行两个整数 x,y，表示询问点 x 到点 y 的最短距离。
树中结点编号从 1 到 n。

输出格式
共 m 行，对于每次询问，输出一行询问结果。

数据范围
2≤n≤10^4,
1≤m≤2×10^4,
0<k≤100,
1≤x,y≤n
输入样例1：
2 2 
1 2 100 
1 2 
2 1
输出样例1：
100
100
输入样例2：
3 2
1 2 10
3 1 15
1 2
3 2
输出样例2：
10
25

思路：

考察LCA问题。

---

参考1：算法训练营进阶篇。

参考2：https://oi-wiki.org/graph/lca/。

最近公共祖先简称 LCA（Lowest Common Ancestor），指有根树中距离2个节点最近的公共祖先。祖先指当前节点到树根路径上的所有节点。

求解LCA的方法有很多，包括暴力搜索法、树上倍增法、RMQ、Tarjan算法等。

LCA问题参考视频讲解：https://www.bilibili.com/video/BV1nE411L7rz?share_source=copy_web。

---

补充一下关于离线与在线查询的区别：

在线做法：边读边做。

离线做法：先读完，再全部处理，最后全部输出。

更直观地讲，就是离线算法途中拿出来的结果就是最终结果的一部分，而在线算法可能到了最后一步才能得到需要的结果，而过程中产生中间结果都是为最后结果的输出而服务的。

参考题解：https://www.acwing.com/solution/content/24569/。

参考题解：https://www.acwing.com/solution/content/9034/。

Tarjan算法离线求解LCA。（建议参考算法训练营的“完美图解”掌握tarjan的具体执行过程细节）

回到题目，注意边是无向的，所以要存两遍。

这里用数组模拟邻接表的形式存储树，与之前稍有不同的是多了边权，还有并查集的知识，忘了的回头复习。
在tarjan函数的深度优先遍历时,将所有点分成三大类：st数组的值作为标志

1. [2] 已经遍历过,且回溯过
2. [1] 正在搜索的分支
3. [0] 还未搜索到的点

其中所有2号点和正在搜索的1号点路径中已经通过并查集合并成一个集合。

在深度优先遍历1号点中的u点的时候，需要把u的查询的另外一个点的最短距离进行计算并存储，最后把u点合并到上一结点的集合，这样确保查询祖宗的时候不出错。

关于tarjan(j);p[j] = u;的顺序说明：如果交换顺序，2号点将无法被并查集合并，必须回溯完再合并，就是说需要把当前节点的所有子节点都处理完，再都合并到父节点中。如果顺序反了，每个节点在并查集的根节点都是它的父节点，都属于独立的集合，就无法正确计算最近公共祖先了，除非这棵树只有一层。

参考题解：https://www.cnblogs.com/JVxie/p/4854719.html。（有图模拟详细过程）

基本流程：

1.任选一个点为根节点，从根节点开始。

2.遍历该点u所有子节点v，并标记这些子节点v已被访问过。

3.若是v还有子节点，返回2，否则下一步。

4.合并v到u上。

5.寻找与当前点u有询问关系的点v。

6.若是v已经被访问过了，则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。

遍历的话需要用到dfs来遍历，至于合并，最优化的方式就是利用并查集来合并两个节点。

时间复杂度：O(n+m)，常数比倍增法大。时间主要看tarjan函数，遍历n个点，处理m次查询，O((n+m)*Alpha(n))，Alpha(n)可近似看成O(1)，所以是O(n+m)。

在仅使用路径压缩优化的情况下，单次调用 find() 函数的时间复杂度为均摊O(1)，而不是O(logn)。

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int,int> PII;
const int N = 10005,M = 2*N;

int n,m;
int h[N],e[M],ne[M],w[M],idx;// w存边权
int p[N];// 并查集数组
int res[2*M];// 存放对应编号的询问答案，需要2倍询问，类似无向图的边
vector<PII> query[N];// 离线Tarjan，存下所有询问
// query[i][first][second] first存查询距离i的另外一个点j，second存查询编号idx
int st[N];// tarjan的标记数组
int dist[N];// 存每个点和1号点的距离

void add(int a,int b,int c){// 加边，带权值
    e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}

void dfs(int u,int fa){// dfs求各编号到1号点的距离dist
    for (int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if (j == fa) continue;
        dist[j] = dist[u] + w[i];// 注意不要写错，u是j的父亲，i对应邻接表的游标idx，是边权w[i]
        dfs(j,u);// 先算父亲，再算儿子
    }
}

int find(int x){// 并查集的查找，路径压缩
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void tarjan(int u){// 求解LCA
    st[u] = 1;
    // u这条路上的根节点的左下的点用并查集合并到根节点
    for (int i = h[u]; ~i;i = ne[i]){// 求dist也可以放在tarjan中进行
        int j = e[i];
        if (!st[j]){// st[j]为0表示还没走过，1表示正在访问，2表示已经访问完且已经回溯过
            tarjan(j);// 往下搜到叶子节点，必须放合并操作之前，先处理询问
            p[j] = u;// 并查集的合并操作，从下面回溯后把u往下搜到的点并入u
        }
    }
    // 对于当前节点u，处理和u相关的所有查询
    for (auto item:query[u]){
        int y = item.first,id = item.second;
        if (st[y] == 2){// 如果和u相关的点y已经访问过且回溯过
            int anc = find(y);// u和y的LCA就是y在并查集的根节点
            // 查找祖宗的时候一并更新路径上所有节点的根节点
            res[id] = dist[u] + dist[y] - 2*dist[anc];
            // 根据询问编号，通过LCA计算u和j的最短距离
        }
    }

    st[u] = 2;// u已经访问过且要回溯，标记为2，放在遍历节点和处理询问之间也行
}

int main(){
    scanf("%d%d",&n,&m);
    memset(h,-1,sizeof h);

    int a,b,c;
    for (int i = 0;i < n-1;i++){// 建图
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c),add(b,a,c);
    }

    // 读入询问
    int e,f;
    for (int i = 0;i < m;i++){
        scanf("%d%d",&e,&f);
        if (e != f){// e = f，距离就是0，不用处理
            query[e].push_back({f,i});// 两个点之前的询问是相互的，和边类似
            query[f].push_back({e,i});
        }
    }
    dfs(1,-1);// 求距离

    for (int i = 1;i <= n;i++) p[i] = i;// 初始化并查集
    tarjan(1);// 从1号点往下搜

    for (int i = 0;i < m;i++) printf("%d\n",res[i]);// 输出每次询问答案
    return 0;
}

7 acwing.840. 模拟散列表（模板题）

维护一个集合，支持如下几种操作：
I x，插入一个数 x；
Q x，询问数 x 是否在集合中出现过；
现在要进行 N 次操作，对于每个询问操作输出对应的结果。

输入格式
第一行包含整数 N，表示操作数量。
接下来 N 行，每行包含一个操作指令，操作指令为 I x，Q x 中的一种。

输出格式
对于每个询问指令 Q x，输出一个询问结果，如果 x 在集合中出现过，则输出 Yes，否则输出 No。
每个结果占一行。

数据范围
1≤N≤10^5
−10^9≤x≤10^9
输入样例：
5
I 1
I 2
I 3
Q 2
Q 5
输出样例：
Yes
No

思路：

哈希表的模板题。

参考：算法笔记。

哈希表是又称散列表，一种以 “key-value” 形式存储数据的数据结构。

可以把哈希表理解为一种高级的数组，这种数组的下标可以是很大的整数，浮点数，字符串甚至结构体。

也就是把复杂的结构（内容庞杂）映射到一个小范围（一般取0~N，N一般较小）。

哈希可以用一句话说明：将元素通过一个函数转换为整数，使得该整数可以尽量唯一地代表这个元素。

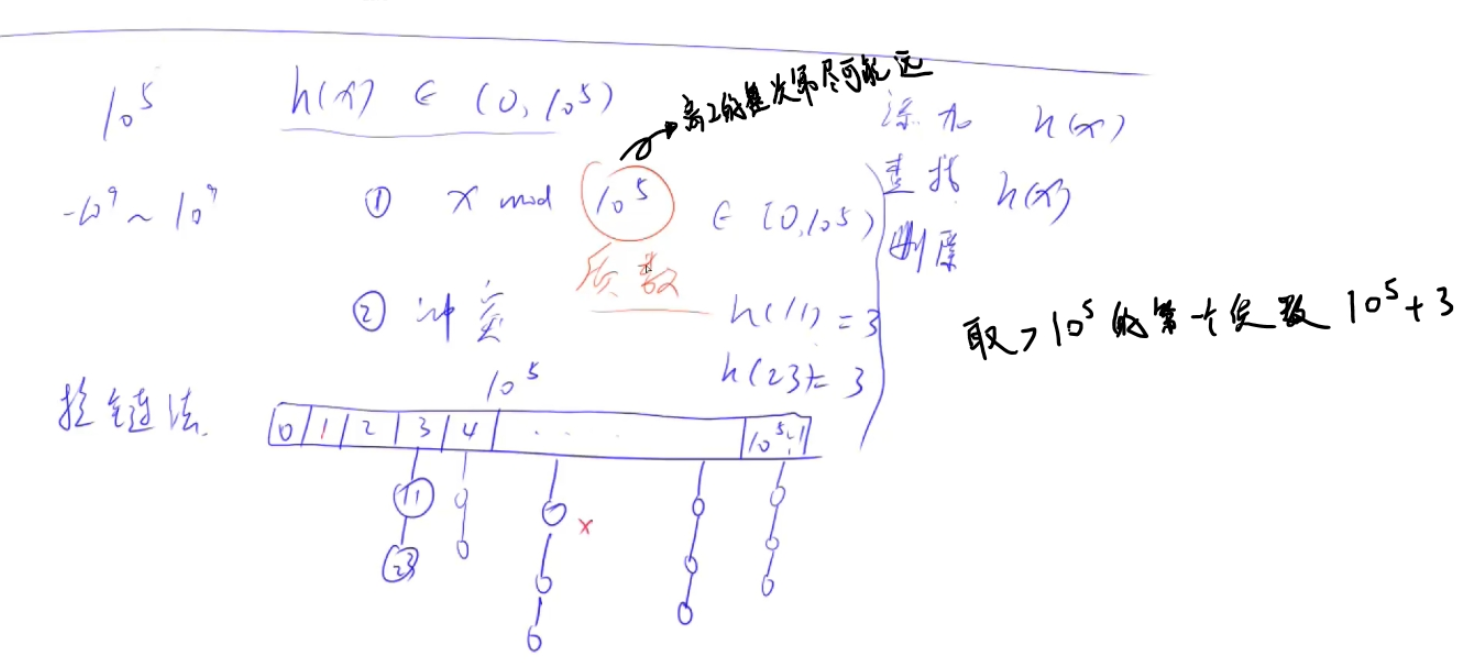
常见的解决冲突的方法（哈希表的存储结构）有：开放寻址法、拉链法。

算法题中的哈希表一般只涉及到添加和查找2种操作，不涉及删除操作。

1.拉链法： 52 ms。时间复杂度：O(n)，处理n次询问。

注意：哈希函数中的模数一般都取成质数且离2的次幂较远。（这样能有效降低冲突概率）

为什么？

如果模数是2的倍数，那么模2余0的数将只会映射到模2余0的位置，同理模2余1的数将只会映射到模2余1的位置，很容易产生冲突。

还是用数组模拟链表，和（三五）树形DP存图的方式一模一样。（忘了的回去复习）

#include <cstdio>
#include <cstring>
#include <algorithm>
const int N = 100003;
int h[N],e[N],ne[N],idx;

void insert(int x){// 通过hash函数插入x
    int k = (x % N + N) % N;// 转正余数
    e[idx] = x,ne[idx] = h[k],h[k] = idx++;// 新节点插入链表中
}

bool find(int x){// 通过hash函数查找x
    int k = (x % N + N) % N;
    for (int i = h[k]; ~i;i = ne[i]){
        if (e[i] == x) return true;
    }
    return false;
}

int main(){
    // 计算hash函数的模数，取离10^5最近的质数，10^5+3
    // for (int i = 100000; ;i++){
    //     bool flag = true;
    //     for (int j = 2;j * j <= i;j++){
    //         if (i % j == 0){
    //             flag = false;
    //             break;
    //         }
    //     }
    //     if (flag){
    //         printf("%d\n",i);
    //         break;
    //     }
    // }
    int n;
    scanf("%d",&n);
    memset(h,-1,sizeof h);// 建立链表前记得置-1

    int x;
    char op[2];// 存1个字符的字符串
    while (n--){// 尽量用scanf读入字符串，忽略回车空格制表符等
        // 这里用字符读入会读到空格！！！
        scanf("%s%d",op,&x);
        if (*op == 'I') insert(x);
        else{
            if (find(x)) puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

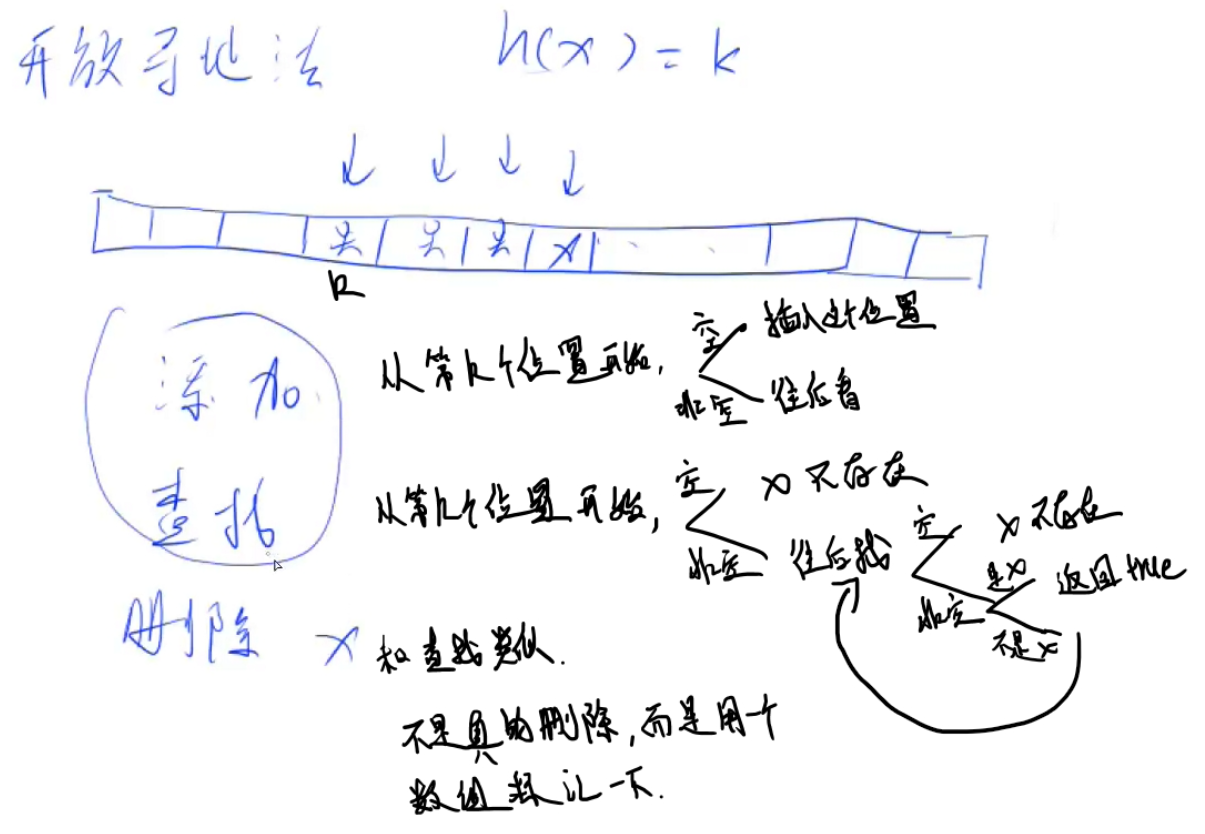
2.开放寻址法： 52 ms。时间复杂度：O(n)，处理n次询问。

开一个一维数组（经验上开数据范围的2到3倍）。

#include <cstdio>
#include <cstring>
#include <algorithm>
const int N = 200003,null = 0x3f3f3f3f;
int h[N];
int find(int x){// 开放寻址法的核心操作
    int k = (x % N + N) % N;
    while (h[k] != null && h[k] != x){
        k ++;
        if (k == N) k = 0;// 找到最后一个空位，返回开头继续找
    }
    return k;
}// 1.如果x在数组h中存在，返回其位置;2.如果x在数组h中不存在，返回下一个空位

int main(){
    // 计算hash函数的模数，取离20^5最近的质数，200003
    // for (int i = 200000; ;i++){
    //     bool flag = true;
    //     for (int j = 2;j * j <= i;j++){
    //         if (i % j == 0){
    //             flag = false;
    //             break;
    //         }
    //     }
    //     if (flag){
    //         printf("%d\n",i);
    //         break;
    //     }
    // }
    int n;
    scanf("%d",&n);
    memset(h,0x3f,sizeof h);// 将h初始化为不在x范围的数null，表示位置没用过
    
    char op[2];
    int x;
    while (n--){
        scanf("%s%d",op,&x);
        int k = find(x);
        if (*op == 'I') h[k] = x;// 返回空位，插入x
        else{
            if (h[k] != null) puts("Yes");
            else puts("No");// 返回空位说明没找到x
        }
    } 
    return 0;
}

3.STL—>unordered_map：91 ms。map：274 ms。

#include <cstdio>
#include <unordered_map>
using namespace std;
unordered_map<int,int> a;
int main()
{
    char s[2];
    int n,x;
    scanf("%d",&n);
    while(n--){
        scanf("%s%d",s,&x);
        if (*s == 'I') a[x] = x;
        else if (a[x] == 0) puts("No");
        else puts("Yes");
    }
    return 0;
}

y总模板：

(1) 拉链法

int h[N], e[N], ne[N], idx;
// 向哈希表中插入一个数
void insert(int x)
{
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++ ;
}

// 在哈希表中查询某个数是否存在
bool find(int x)
{
    int k = (x % N + N) % N;
    for (int i = h[k]; i != -1; i = ne[i])
        if (e[i] == x)
            return true;

    return false;
}

(2) 开放寻址法

  int h[N];
// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
int find(int x)
{
    int t = (x % N + N) % N;
    while (h[t] != null && h[t] != x)
    {
        t ++ ;
        if (t == N) t = 0;
    }
    return t;
}

这是蓝桥杯学习总结系列的最后一篇！蓝桥杯系列正式完结！

整理题目86道，完成题解85篇，竞赛内容10章，系列文章40篇，时间跨度134天。