算法基础课笔记（三一）

例题：907. 区间覆盖（模板题）

给定 N 个闭区间 [ai,bi] 以及一个线段区间 [s,t]，请你选择尽量少的区间，将指定线段区间完全覆盖。
输出最少区间数，如果无法完全覆盖则输出 −1。

输入格式
第一行包含两个整数 s 和 t，表示给定线段区间的两个端点。
第二行包含整数 N，表示给定区间数。
接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式
输出一个整数，表示所需最少区间数。

如果无解，则输出 −1。

数据范围
1≤N≤10^5,
−10^9≤ai≤bi≤10^9,
−10^9≤s≤t≤10^9
输入样例：
1 5
3
-1 3
2 4
3 5
输出样例：
2

证明：在剩下所有能覆盖start的区间中，选择右端点最大的区间，则一定会比前面的选择最优，更快达到end，所以该做法一定是最优。

#include <iostream>
#include <algorithm>
using namespace std;
#define IOS \
    ios::sync_with_stdio(false); \
    cin.tie(0); \
    cout.tie(0)
const int N = 1e5+ 5;
typedef pair<int,int> PII;
PII range[N];

int main(){
    IOS;
    int st,ed;
    cin >> st >> ed;
    int n;
    cin >> n;

    int l,r;
    for (int i = 0;i < n;i ++){
        cin >> l >> r;
        range[i] = {l,r};
    }

    sort(range,range + n);
    int res = 0;bool success = false;// res表示选择区间数，success标志是否成功覆盖
    for (int i = 0;i < n;i ++){// 在所有能覆盖st的区间中选择右端点最大的区间
        int j = i,r = -0x3f3f3f3f;// 双指针算法
        // 双指针找到第一个开始不能覆盖st的区间，之前的都能覆盖
        while (j < n && range[j].first <= st){
            r = max(r,range[j].second);// 寻找过程中不断更新最大的右端点r
            j ++;
        }
        
        if (r < st){// 若最大右端点不能到达上次st，说明区间不能继续往右延伸
            res = -1;break;
        }
        res ++;
        if (r >= ed){// 若最大右端点能到达ed，说明可以成功覆盖整段目标区间
            success = true;break;
        }
        st = r;// 最大右端点作为新的st
        i = j - 1;// for循环中有i++
    }
    if (!success) res = -1;
    cout << res << '\n';
    return 0;
}

5.2：Huffman树

赫夫曼树（Huffman tree），别名“哈夫曼树”、“最优树”以及“最优二叉树”。

《算法笔记》有介绍经典例题—合并果子。

图解哈夫曼树及编码： https://blog.csdn.net/weixin_42060232/article/details/107762926。

哈夫曼树介绍： http://c.biancheng.net/view/3398.html。

例题：148. 合并果子（模板题）

在一个果园里，达达已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。
达达决定把所有的果子合成一堆。
每一次合并，达达可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。

可以看出，所有的果子经过 n−1 次合并之后，就只剩下一堆了。
达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家，所以达达在合并果子时要尽可能地节省体力。

假定每个果子重量都为 1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使达达耗费的体力最少，并输出这个最小的体力耗费值。
    
例如有 3 种果子，数目依次为 1，2，9。
可以先将 1、2 堆合并，新堆数目为 3，耗费体力为 3。
接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 12，耗费体力为 12。
所以达达总共耗费体力=3+12=15。
可以证明 15 为最小的体力耗费值。

输入格式
输入包括两行，第一行是一个整数 n，表示果子的种类数。
第二行包含 n 个整数，用空格分隔，第 i 个整数 ai 是第 i 种果子的数目。

输出格式
输出包括一行，这一行只包含一个整数，也就是最小的体力耗费值。
输入数据保证这个值小于 2^31。

数据范围
1≤n≤10000,
1≤ai≤20000
输入样例：
3 
1 2 9 
输出样例：
15

本题和区间DP中的石子合并非常像，石子合并中要求只能合并相邻石堆，本题没有限制，石堆规模是300，比较小，本题数据规模大。

要注意区别：合并相邻石堆的性质决定了大的区间可以由小的区间状态转移而来，所以是区间DP；合并任意两个果子堆，使得消耗体力（WPL）最小，应该是哈夫曼树。

算法：哈夫曼树。

哈夫曼树不一定是完全二叉树。叶子节点就是需要合并的堆。

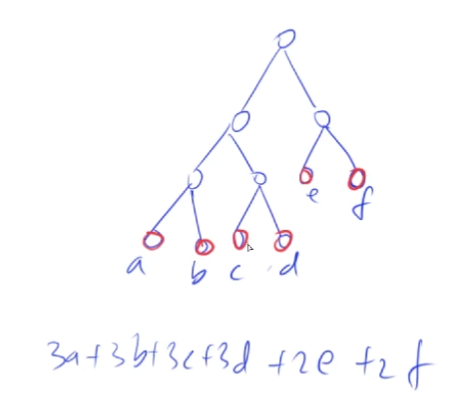
通过哈夫曼树计算最小消耗体力：

其实这里的最小消耗体力就是结点的带权路径长度（WPL）。

不难得到哈夫曼树的构建原则：权重越大的结点离树根越近。

构建哈夫曼树：

根据直观的理解，应该先找到节点值最小的两个，构造成子树，这两个节点唯一能确定的是层数肯定是最大的，这两个节点之和作为的父节点值。然后不断重复过程。我们发现这就是贪心寻找局部最优解的过程，最终得到的WPL就是全局最优解。

通过反证法很容易得出：上一层节点的权值肯定大于等于下一层节点的权值，否则它们可以交换位置减少体力消耗。

对于权值最小的两个点：深度一定是最大的，且可以互为兄弟。

哈夫曼树的构成并不唯一，在同一层次的两个叶子节点可以交换顺序，但是WPL是唯一的。

#include <queue>
#include <cstdio>
using namespace std;

int main(){// 小根堆
    priority_queue<int,vector<int>,greater<int> > heap;
    int n;
    scanf("%d", &n);
    
    int x;
    for (int i = 0;i < n;i ++){
        scanf("%d", &x);
        heap.push(x);
    }
    // n个堆合并n-1次
    int res = 0;
    for (int i = 1; i < n; i ++ ){
        int a = heap.top();heap.pop();
        int b = heap.top();heap.pop();
        res += a + b;
        heap.push(a+b);
    }
    printf("%d\n",res);
    return 0;
}