4.补充:差分算法
参考资料:https://oi-wiki.org/basic/prefix-sum/。
差分是一种和前缀和相对的策略,可以当做是求和的逆运算。
墙推:前缀和与差分算法总结
4.1 acwing.797. 差分(一维差分)
模板题, Hulu面试题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| 输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 m 行,每行包含三个整数 l,r,c,表示一个操作。
输出格式
共一行,包含 n 个整数,表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2
|
思路:
差分可以维护多次对序列的一个区间加上一个数,并在最后询问某一位的数或是多次询问某一位的数。
注意:修改操作一定要在查询操作之前。
对于给定的序列a[1],a[2],…,a[n],我们构造一个差分数组b[n],使得:a[i] = b[1]+b[2]+...+b[i],也就
是说a[N]是b[N]的前缀和数组。
$\text { 这种策略的定义是令 } b_{i}=\left\{\begin{array}{ll}
a_{i}-a_{i-1} & i \in[2, n] \\
a_{1} & i=1
\end{array}\right.$
核心操作:将a[L~R]全部加上c,等价于:b[L] += c,b[R+1] -= c。
简单证明一下:
- 对于a[1~L-1]:没有影响;
- 对于a[L~R]:b[L] += c,所以a[L~R] += c;
- 对于a[R+1~n]:b[L] += c,b[R+1] -= c,所以无影响。
初始化差分数组b[n]:相当于按a[1~1],a[2~2],a[n-n]的顺序分别加上一个给出的数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| #include <cstdio>
using namespace std;
const int N = 100010;
int n,m;
int a[N],b[N];
void insert(int l,int r,int c){
b[l] += c,b[r+1] -= c;
}
int main(){
scanf("%d%d",&n,&m);
for (int i = 1;i <= n;i++){
scanf("%d",&a[i]);
insert(i,i,a[i]);
}
int l,r,c;
for (int i = 0;i < m;i++){
scanf("%d%d%d",&l,&r,&c);
insert(l,r,c);
}
for (int i = 1;i <= n;i++){
a[i] = a[i-1] + b[i];
printf("%d ",a[i]);
}
return 0;
}
|
4.2 acwing.798. 差分矩阵(二维差分)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| 输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2
|
思路:
对于给定的矩阵a[N][N],我们构造一个差分矩阵b[N][N],使得:a[i][j]是b[i][j]的二维前缀和。
核心操作:给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素a[i][j]加上c。
等价于:B[x1, y1] += c, B[x2 + 1, y1] -= c, B[x1, y2 + 1] -= c, B[x2 + 1, y2 + 1] += c。
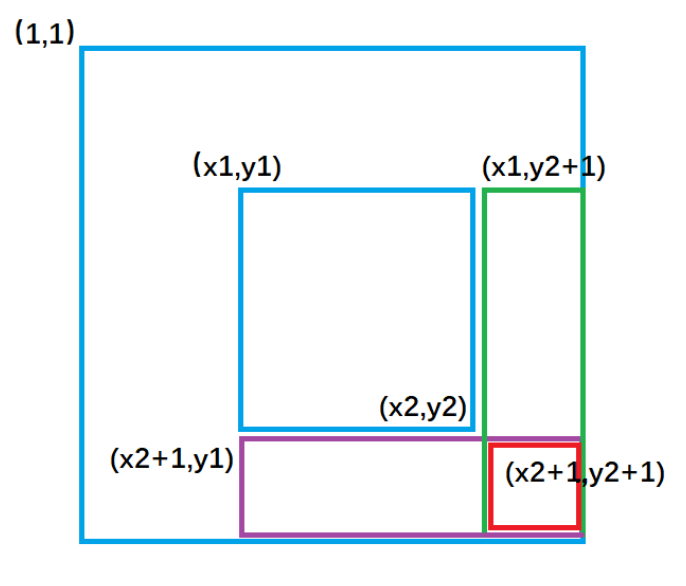
b[x1][ y1 ] +=c ; 让整个a数组中(x1,y1)到大矩形右下角范围的元素都加上了c。
b[x1][y2+1]-=c ; 让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y1]- =c ; 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y2+1]+=c; 对应图4,让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再
加上一次c,才能使其恢复。
初始化差分数组b[N][N]:相当于按{(1,1),(1,1)},{(1,2),(1,2)},{(n,m),(n,m)}的顺序分别加上一个给出的数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1010;
int n,m,q;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c){
b[x1][y1] += c;
b[x1][y2+1] -= c;
b[x2+1][y1] -= c;
b[x2+1][y2+1] += c;
}
int main(){
scanf("%d%d%d",&n,&m,&q);
for (int i = 1;i <= n;i++)
for (int j = 1;j <= m;j++){
scanf("%d",&a[i][j]);
insert(i,j,i,j,a[i][j]);
}
int x1,y1,x2,y2,c;
while (q--){
scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
insert(x1,y1,x2,y2,c);
}
for (int i = 1;i <= n;i++){
for (int j = 1;j <= m;j++){
a[i][j] = a[i-1][j] + a[i][j-1] - a[i-1][j-1] + b[i][j];
printf("%d ",a[i][j]);
}
puts("");
}
return 0;
}
|
差分知识总结:

前缀和与差分模板总结(来自于yls视频)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
S[i] = a[1] + a[2] + ... a[i]
从a[l]到a[r]的和为:a[l] + ... + a[r] = S[r] - S[l - 1]
S[i, j] = 第i行j列格子左上部分所有元素的和
S{x,y} = S{x-1,y}+S{x,y-1}-S{x-1,y-1}+a{x,y}
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
给区间[l, r]中的每个数加上c:
B[l] += c, B[r + 1] -= c
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
B[x1, y1] += c, B[x2 + 1, y1] -= c, B[x1, y2 + 1] -= c, B[x2 + 1, y2 + 1] += c
|
4.3 acwing.1232. 三体攻击(三维差分,困难)
第九届蓝桥杯省赛C++A组,第九届蓝桥杯省赛JAVAA组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| 三体人将对地球发起攻击。
为了抵御攻击,地球人派出了 A×B×C 艘战舰,在太空中排成一个 A 层 B 行 C 列的立方体。
其中,第 i 层第 j 行第 k 列的战舰(记为战舰 (i,j,k))的生命值为 d(i,j,k)。
三体人将会对地球发起 m 轮“立方体攻击”,每次攻击会对一个小立方体中的所有战舰都造成相同的伤害。
具体地,第 t 轮攻击用 7 个参数 lat,rat,lbt,rbt,lct,rct,ht 描述;
所有满足 i∈[lat,rat],j∈[lbt,rbt],k∈[lct,rct] 的战舰 (i,j,k) 会受到 ht 的伤害。
如果一个战舰累计受到的总伤害超过其防御力,那么这个战舰会爆炸。
地球指挥官希望你能告诉他,第一艘爆炸的战舰是在哪一轮攻击后爆炸的。
输入格式
第一行包括 4 个正整数 A,B,C,m;
第二行包含 A×B×C 个整数,其中第 ((i−1)×B+(j−1))×C+(k−1)+1 个数为 d(i, j, k);
第 3 到第 m+2 行中,第 (t − 2) 行包含 7 个正整数 lat, rat, lbt, rbt, lct, rct, ht。
输出格式
输出第一个爆炸的战舰是在哪一轮攻击后爆炸的。
保证一定存在这样的战舰。
数据范围
1≤A×B×C≤10^6,
1≤m≤10^6,
0≤d(i, j, k), ht≤10^9,
1≤lat≤rat≤A,
1≤lbt≤rbt≤B,
1≤lct≤rct≤C
层、行、列的编号都从 1 开始。
输入样例:
2 2 2 3
1 1 1 1 1 1 1 1
1 2 1 2 1 1 1
1 1 1 2 1 2 1
1 1 1 1 1 1 2
输出样例:
2
样例解释
在第 2 轮攻击后,战舰 (1,1,1) 总共受到了 2 点伤害,超出其防御力导致爆炸。
|
思路:
考察二分、前缀和与差分。(PS:本题与树状数组和线段树无关)
问题:从第几轮攻击开始,某个格子的生命小于0。
由题意知道生命值一定是递减的,满足二分的条件。如果从头开始遍历,比较慢,所以用二分优化。
由于是立方体,所以用到三维差分,
设读入的数据存入S[N][N][N](这里为了方便展开成三维,代码中做了映射处理,实际只有一维),构造差
分数组b[N][N][N]。
类比一维和二维,我们得到三维前缀和公式:用到三个集合的容斥原理,奇数个-1就+,偶数个-1就-
S{x,y,z} = S{x-1,y,z}+S{x,y-1,z}+S{x,y,z-1}-S{x-1,y-1,z}-S{x,y-1,z-1}-S{x-1,y,z-1}+S{x-1,y-1,z-1}+b{x,y,z}
由此可以反求出b{x,y,z},构造差分数组。
同理类比一维和二维,我们得到三维差分公式:从(x1, y1,z1)到(x2,y2,z2)范围内的S{i,j,k}都减去一个数h
注意这里是减去一个数h!!!
b{x1,y1,z1} -= h,b{x1,y1,z2+1} += h,b{x1,y2+1,z1} += h,b{x1,y2+1,z2+1} -= h,
b{x2+1,y1,z1} += h,b{x2+1,y1,z1+1} -= h,b{x2+1,y2+1,z2+1} += h 奇数个+1就+=h,偶数个就-=h
由于题目只给出了A×B×C的范围,不知道每个维度具体范围,所以直接开一维数组,需要映射处理一下。
二维映射:AXB,(i,j)-->i*B+j;三维映射:AXBXC,(i,j,k)-->(i*B+j)*C+k
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
| #include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 2000010;
int A,B,C,m;
LL s[N],b[N],bp[N];
int op[N>>1][7];
int d[8][4] = {
{0,0,0,1},
{0,0,1,-1},
{0,1,0,-1},
{0,1,1,1},
{1,0,0,-1},
{1,0,1,1},
{1,1,0,1},
{1,1,1,-1}
};
int get(int i,int j,int k){
return (i*B+j)*C+k;
}
bool check(int mid){
memcpy(b,bp,sizeof b);
for (int i = 1;i <= mid;i++){
int x1 = op[i][0],x2 = op[i][1],y1 = op[i][2];
int y2 = op[i][3],z1 = op[i][4],z2 = op[i][5];
int h = op[i][6];
b[get(x1,y1,z1)] -= h;
b[get(x1,y1,z2 + 1)] += h;
b[get(x1,y2 + 1,z1)] += h;
b[get(x1,y2 + 1,z2 + 1)] -= h;
b[get(x2 + 1,y1,z1)] += h;
b[get(x2 + 1,y1,z2 + 1)] -= h;
b[get(x2 + 1,y2 + 1,z1)] -= h;
b[get(x2 + 1,y2 + 1,z2 + 1)] += h;
}
memset(s,0,sizeof s);
for (int i = 1;i <= A;i++)
for (int j = 1;j <= B;j++)
for (int k = 1;k <= C;k++)
{
s[get(i,j,k)] = b[get(i,j,k)];
for (int u = 1;u < 8;u++){
int x = i - d[u][0],y = j - d[u][1],z = k - d[u][2],t = d[u][3];
s[get(i,j,k)] -= s[get(x,y,z)]*t;
}
if (s[get(i,j,k)] < 0) return true;
}
return false;
}
int main(){
scanf("%d%d%d%d",&A,&B,&C,&m);
for (int i = 1;i <= A;i++)
for (int j = 1;j <= B;j++)
for (int k = 1;k <= C;k++) scanf("%lld",&s[get(i,j,k)]);
for (int i = 1;i <= A;i++)
for (int j = 1;j <= B;j++)
for (int k = 1;k <= C;k++)
for (int u = 0;u < 8;u++){
int x = i - d[u][0],y = j - d[u][1],z = k - d[u][2],t = d[u][3];
bp[get(i,j,k)] += s[get(x,y,z)] * t;
}
for (int i = 1;i <= m;i++)
for (int j = 0;j < 7;j++) scanf("%d",&op[i][j]);
int l = 1,r = m;
while (l < r){
int mid = l+r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
printf("%d\n",r);
return 0;
}
|
insert的写法:
1
2
3
4
5
6
7
8
9
10
11
| void insert(LL b[],int x1,int x2,int y1,int y2,int z1,int z2,int c)
{
b[get(x1, y1, z1) ] +=c;
b[get(x1, y1, z2+1)] -=c;
b[get(x1, y2+1, z1) ] -=c;
b[get(x1, y2+1, z2+1)] +=c;
b[get(x2+1,y1, z1) ] -=c;
b[get(x2+1,y1, z2+1)] +=c;
b[get(x2+1,y2+1, z1) ] +=c;
b[get(x2+1,y2+1, z2+1)] -=c;
}
|
代码太长的debug方式:
- 使用文本对比工具,比如Vscode自带的,ctrl选择两个文件,右键比较,也可以用专业软件像beyond compare
- 与AC代码比较,一段一段CV,二分找到错误点



