寒假每日一题入门题（一）

Day_01 104.货仓选址

这题考察绝对值不等式

参考题解

由绝对值不等式可证明：
将n个数两两分组，如果n是奇数，货仓取中位数时取到不等式的等号，此时为最小值；如果n是偶数，货仓取中间两个数的中间即可。
结论：中位数就是此题的最优解。

---

算法1：排序+中位数

时间复杂度：$O(nlogn)$

中位数有非常优秀的性质，比如说在这道题目中，每一个点到中位数的距离，都是满足全局的最有性，而不是局部最优性。

具体的来说，我们设在仓库左边的所有点，到仓库的距离之和为p,右边的距离之和则为q，那么我们就必须让p+q的值尽量小。

当仓库向左移动的话，p会减少x，但是q会增加n−x，所以说当为仓库中位数的时候,p+q最小。

还是同样的一句话，画图理解很重要。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N];
int n;
int main()
{
    cin >> n;
    for (int i = 0;i < n;i ++) cin >> a[i];
    sort(a,a+n);
    int res = 0;
    for (int i = 0;i < n;i ++) res += a[i] - a[i>>1];
    // ==> res += abs(a[i] - a[n>>1])
    cout << res;
    return 0;
}

---

将 abs(a[i] - a[n >> 1]) 改为 a[i] - a[i >> 1]也可以 AC（这样可以不用取绝对值）

证明如下：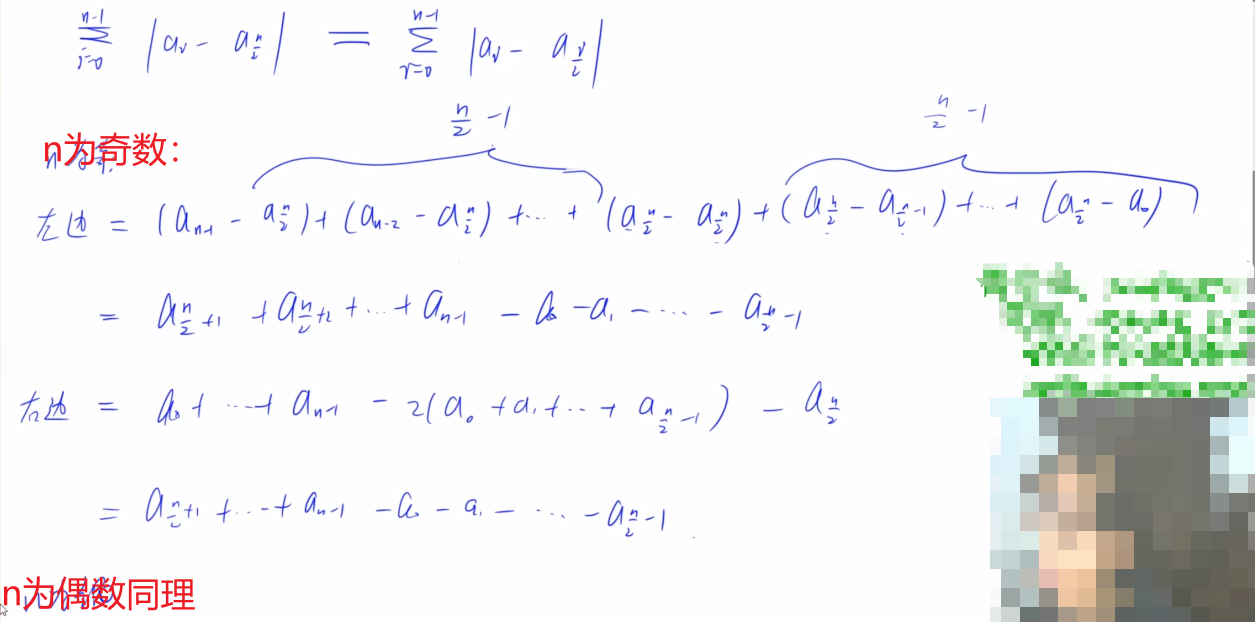

算法2：快速选择+中位数

快速选择函数nth_element(数组初位置，寻找元素，数组末位置)（STL）

C++的STL库中的nth_element()方法，默认是求区间第k小的（划重点）。

举个栗子求第3小，对于 a[9]={4,7,6,9,1,8,2,3,5};

nth_element(a,a+2,a+9)，将下标为2，也就是第3个数放在正确的位置，求的是第3小的数a[2]。（下标从零开始）

nth_element(a,a+k,a+n)，函数只是把下标为k的元素放在了正确位置，对其它元素并没有排序，当然k左边元素都小于等于它，右边元素都大于等于它，所以可以利用这个函数快速定位某个元素。

那求第k大时呢？我们可以转化成求第n-k+1小，此时下标应该是n - k。

nth_element(a,a+n-k,a+n)，将下标为n-k，也就是第n-k+1个数放在正确的位置，求的是第k大的数a[n-k]。

时间复杂度：$O(n)$

#include<iostream>
#include<algorithm>
using namespace std;
int p[100010];
int main(){
    int n,s=0;
    cin>>n;
    for(int i=0;i<n;i++) cin>>p[i];
    nth_element(p,p+n/2,p+n);
    for(int i=0;i<n;i++) s+=abs(p[i]-p[n/2]);
    cout<<s<<endl;
    return 0;
}