4.4 acwing.1241. 外卖店优先级
第十届蓝桥杯省赛C++A/C组,第十届蓝桥杯省赛JAVAA/B/C组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| “饱了么”外卖系统中维护着 N 家外卖店,编号 1∼N。
每家外卖店都有一个优先级,初始时 (0 时刻) 优先级都为 0。
每经过 1 个时间单位,如果外卖店没有订单,则优先级会减少 1,最低减到 0;而如果外卖店有订单,则优先级不减反加,每有一单优先级加 2。
如果某家外卖店某时刻优先级大于 5,则会被系统加入优先缓存中;如果优先级小于等于 3,则会被清除出优先缓存。
给定 T 时刻以内的 M 条订单信息,请你计算 T 时刻时有多少外卖店在优先缓存中。
输入格式
第一行包含 3 个整数 N,M,T。
以下 M 行每行包含两个整数 ts 和 id,表示 ts 时刻编号 id 的外卖店收到一个订单。
输出格式
输出一个整数代表答案。
数据范围
1≤N,M,T≤10^5,
1≤ts≤T,
1≤id≤N
输入样例:
2 6 6
1 1
5 2
3 1
6 2
2 1
6 2
输出样例:
1
样例解释
6 时刻时,1 号店优先级降到 3,被移除出优先缓存;2 号店优先级升到 6,加入优先缓存。
所以是有 1 家店 (2 号) 在优先缓存中。
|
思路:
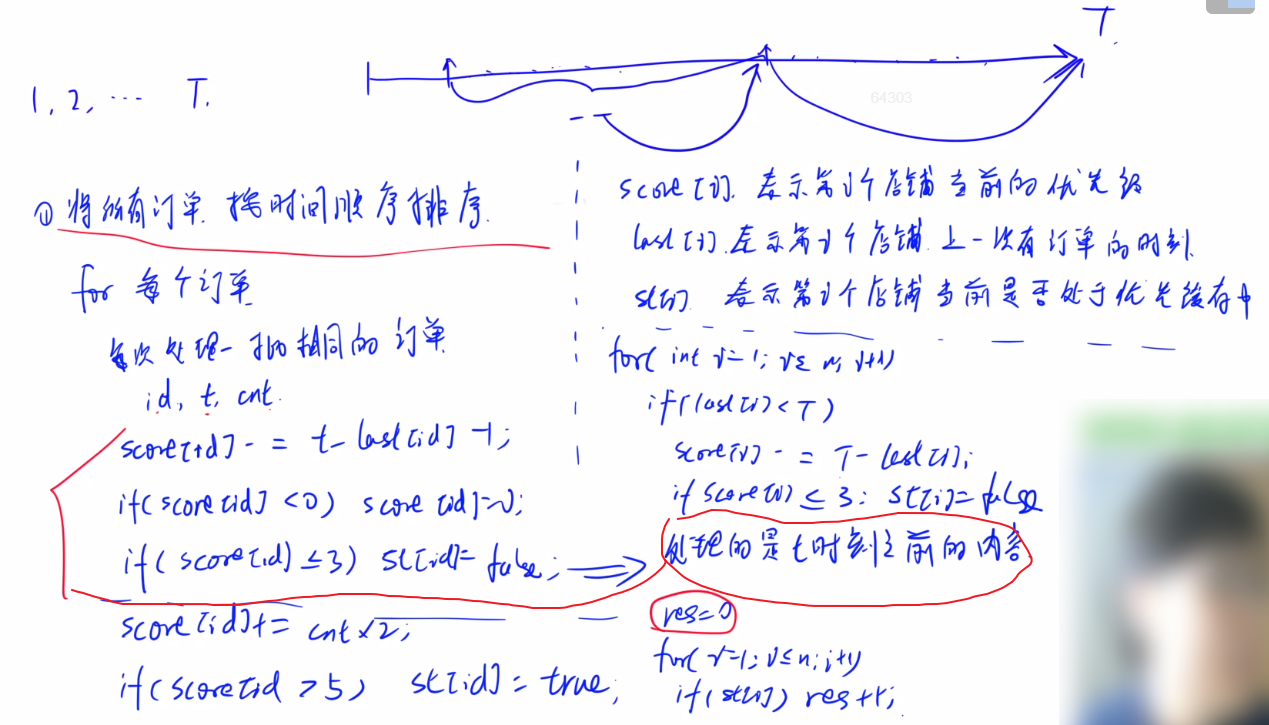
首先想到的就是直接按照题目要求模拟。

对于每个时间点,对有订单和无订单的店分别处理优先级,处理完之后判断状态,最后遍历所有店,输出在优
先缓存中的店的数量。
这种做法比较暴力,计算时间复杂度为O(T*N),也就是10^10。肯定过不了,只能拿到部分分数。
想想怎么优化?
由于时间段被分割成不连续的一段段,因为不可能每个时刻每个店都有外卖,我们可以压缩没有外卖的时间,
在有外卖的时刻统一处理所有店的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| #include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
const int N = 100010;
int score[N],last[N];
bool st[N];
PII order[N];
int main(){
int n,m,T;
scanf("%d%d%d",&n,&m,&T);
for (int i = 0;i < m;i++) scanf("%d %d",&order[i].x,&order[i].y);
sort(order,order + m);
for (int i = 0;i < m;){
int j = i;
while (j < m && order[i] == order[j]) j++;
int cnt = j-i;
int t = order[i].x,id = order[i].y;
i = j;
score[id] -= t - last[id] - 1;
if (score[id] < 0) score[id] = 0;
if (score[id] <= 3) st[id] = false;
score[id] += cnt*2;
if (score[id] > 5) st[id] = true;
last[id] = t;
}
for (int i = 1;i <= n;i++){
if (last[i] < T){
score[i] -= T - last[i];
if (score[i] <= 3) st[i] = false;
}
}
int res = 0;
for (int i = 1;i <= n;i++) res += st[i];
printf("%d\n",res);
return 0;
}
|
4.5 acwing.788. 逆序对的数量(模板题)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| 给定一个长度为 n 的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第 i 个和第 j 个元素,如果满足 i<j 且 a[i]>a[j],则其为一个逆序对;否则不是。
输入格式
第一行包含整数 n,表示数列的长度。
第二行包含 n 个整数,表示整个数列。
输出格式
输出一个整数,表示逆序对的个数。
数据范围
1≤n≤100000
输入样例:
6
2 3 4 5 6 1
输出样例:
5
|
思路:
首先提一下暴力做法,就是直接两层for循环,遍历数组求解逆序对数量,时间复杂度O(n^2)。
再来优化,这题考察归并排序,利用分治思想。
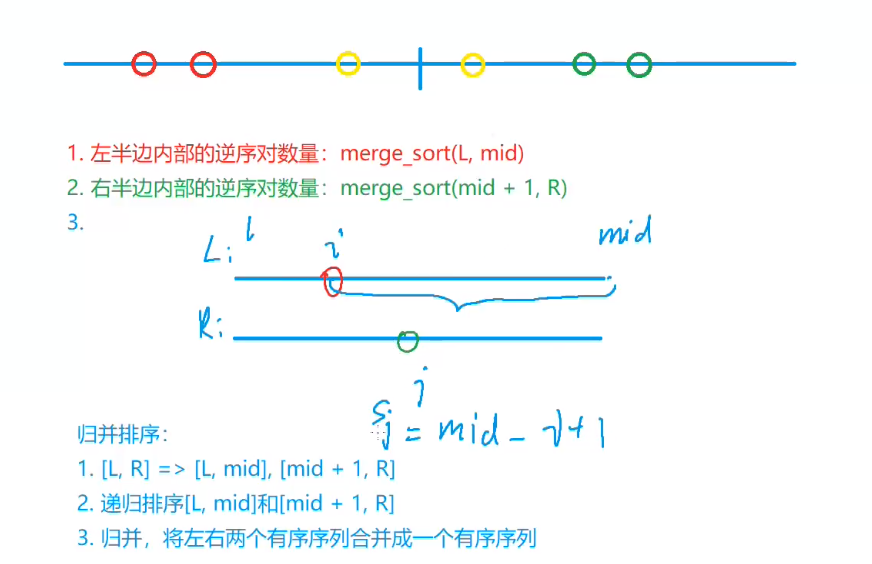
我们先将序列从中间分开,按三种情况计算逆序对数量。
将逆序对分成三类:
1.两个元素都在左边;2.两个元素都在右边;3.两个元素一个在左一个在右;
然后计算逆序对的数量(序列):
- 递归算左边的;
- 递归算右边的;
- 算一个左一个右的;
- 把他们加到到一起。
参考讲解视频。
我们将单调递增的数组称为有序的。
归并排序的过程,其实也就是将逆序变成有序的过程,就是消灭逆序对。
只要把从逆序到有序的交换次数记下来,就是逆序对的数量。
涉及到交换元素的排序,首先想到的就是冒泡排序了,这是比暴力做法相对优化一步的做法了,但是不如归并
排序。对于冒泡排序,只要记录交换次数就行了。
这题实际上是归并排序的经典应用。
归并过程:1.将数组一分为二;2.递归划分数组,直到两边只有一个元素(此时有序);3.归并,注意只有两边都是有序的才能进行,无序则必须递归划分直到有序。
归并排序,时间复杂度当然是O(n*logn)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
int n,q[N],tmp[N];
LL merge_sort(int l,int r){
if (l >= r) return 0;
int mid = l + r >> 1;
LL res = merge_sort(l,mid) + merge_sort(mid+1,r);
int k = 0,i = l,j = mid+1;
while (i <= mid && j <= r){
if (q[i] <= q[j]) tmp[k++] = q[i++];
else{
tmp[k++] = q[j++];
res += mid - i + 1;
}
}
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
for (int i = l,j = 0;i <= r;i++,j++) q[i] = tmp[j];
return res;
}
int main(){
cin >> n;
for (int i = 0;i < n;i++) cin >> q[i];
cout << merge_sort(0,n-1) << endl;
return 0;
}
|




