grant's Blog

记录生活中的点点滴滴

蓝桥杯学习总结（三六）

发表于 更新于 分类于 ，   阅读次数： Valine：
本文字数： 5.5k 阅读时长 ≈ 5 分钟

2.习题

2.1 acwing.1226. 包子凑数

第八届蓝桥杯省赛C++A/B组,第八届蓝桥杯省赛JAVAA/B组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
小明几乎每天早晨都会在一家包子铺吃早餐。
他发现这家包子铺有 N 种蒸笼，其中第 i 种蒸笼恰好能放 Ai 个包子。
每种蒸笼都有非常多笼，可以认为是无限笼。
每当有顾客想买 X 个包子，卖包子的大叔就会迅速选出若干笼包子来，使得这若干笼中恰好一共有 X 个包子。
比如一共有 3 种蒸笼，分别能放 3、4 和 5 个包子。
当顾客想买 11 个包子时，大叔就会选 2 笼 3 个的再加 1 笼 5 个的（也可能选出 1 笼 3 个的再加 2 笼 4 个的）。
当然有时包子大叔无论如何也凑不出顾客想买的数量。
比如一共有 3 种蒸笼，分别能放 4、5 和 6 个包子。
而顾客想买 7 个包子时，大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。

输入格式
第一行包含一个整数 N。
接下来 N 行，每行包含一个整数 Ai。

输出格式
输出一个整数代表答案。
如果凑不出的数目有无限多个，输出INF。

数据范围
1≤N≤100,
1≤Ai≤100
输入样例1：
2
4
5
输出样例1：
6
输入样例2：
2
4
6
输出样例2：
INF
样例解释
对于样例1，凑不出的数目包括： 1, 2, 3, 6, 7, 11。
对于样例2，所有奇数都凑不出来，所以有无限多个。

思路：

参考题解：https://www.acwing.com/solution/content/17888/。

和1205. 买不到的数目有相似的地方，一样会用到裴蜀定理。

由1205得到结论：（可以当公式记忆）

如果 a,b 均是正整数且互质，那么由 ax+by,x≥0,y≥0不能凑出的最大数是 (a−1)(b−1)−1=a*b - a - b.

题目一看，是个组合问题，是完全背包问题的变形：有几个物品，每个物品无限个，每个物品选任意个，能否凑到某个重量。

任意两个数的组合必定是他们gcd的倍数，同样可以推广到更多数：如果这些数的gcd是d，那么他们的组合是d的倍数。如果d不是1，那么必然有无限个数无法被组合出来，答案是INF；如果d是1，那么两个数a,b，最大不能表示出来的数是：(a−1)(b−1)−1。当数字更多的时候，这个上界必然更小（可选的数字变多了），而99和98是100内最大的互质的数，所以这个上界选择10000。

那么下面的事情就是看这么多数中有多少个不能被组合出来，回到了刚开始分析的完全背包问题：

忘记了完全背包问题的复习一下。

1.状态定义:
$d p(i, j)$ 表示前选 $i$ 项物品任意个，重量为 $j$, 属性为能否达到重量 $j($ true $/$ false $)$

2.状态转移:
集合分析法：由最后不同的一步来划分集合，在重量为 $j$ 的时候，第 $i$ 个物品选了几件。 $d p(i, j)=d p(i-1, j)|d p(i-1, j-w(i))| \ldots | d p(i-1, j-k w(i))(k<=j / w(i))$
但是, 完全背包问题有个特殊的地方，那就是状态重叠： $d p(i, j-w(i))$ 是由 $d p(i-1, j-w(i))|d p(i-1, j-2 w(i)) \ldots| d p(i-1, j-k * w(i))(k<=j /w(i))$
转移过来, 仔细看上下两个式子就会发现 $d p(i, j-w(i))$ 的状态就是 $d p(i, j)$ 后面一大部分。
所以最终方程为 $: d p(i, j)=d p(i-1, j) | d p(i, j-w(i))(w(i)<=j)$。

取“或”，因为只要有一种情况能凑出来就能达到，dp(i,j)是true。

算法1：完全背包二维做法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 105,M = 10000;// 无法被组合出的数上限是10000
int n;
int a[N];
bool dp[N][M];

int gcd(int a,int b){
    return b ? gcd(b,a%b) : a;
}
int main(){
    scanf("%d",&n);
    int d = 0;
    for (int i = 1;i <= n;i++){
        scanf("%d",&a[i]);
        d = gcd(d,a[i]);// 求a数组的最大公约数
    }

    if (d != 1) puts("INF");
    else{
        dp[0][0] = true;// dp[0][0]初始化为true，重量为0一定能组合出来，什么都不选
        for (int i = 1;i <= n;i++)
            for (int j = 0;j <= M;j++){// j从0开始枚举
                dp[i][j] = dp[i-1][j];
                if (j >= a[i]) dp[i][j] |= dp[i][j-a[i]];
            }
        
        int res = 0;
        for (int j = 1;j <= M;j++){// j从1开始枚举，因为j=0肯定能组合出来
            if (!dp[n][j]) res++;
        }
        printf("%d\n",res);
    }
    return 0;
}

算法2：完全背包一维优化。（DP数组只依赖2层，第2维计算j只依赖比它小的数，可以一维优化）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 105,M = 10000;// 无法被组合出的数上限是10000
int n;
int a[N];
bool dp[M];

int gcd(int a,int b){
    return b ? gcd(b,a%b) : a;
}
int main(){
    scanf("%d",&n);
    int d = 0;
    for (int i = 1;i <= n;i++){
        scanf("%d",&a[i]);
        d = gcd(d,a[i]);
    }

    if (d != 1) puts("INF");
    else{
        dp[0] = true;// dp[0][0]初始化为true，重量为0一定能组合出来，什么都不选
        for (int i = 1;i <= n;i++)// 一维优化，j直接从a[i]开始枚举
            for (int j = a[i];j <= M;j++) dp[j] |= dp[j-a[i]];
        
        int res = 0;
        for (int j = 1;j <= M;j++){
            if (!dp[j]) res++;
        }
        printf("%d\n",res);
    }
    return 0;
}

2.2 acwing.1070. 括号配对

《信息学奥赛一本通》

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Hecy 又接了个新任务：BE 处理。
BE 中有一类被称为 GBE。
以下是 GBE 的定义：
空表达式是 GBE
如果表达式 A 是 GBE，则 [A] 与 (A) 都是 GBE
如果 A 与 B 都是 GBE，那么 AB 是 GBE
下面给出一个 BE，求至少添加多少字符能使这个 BE 成为 GBE。
注意：BE 是一个仅由 (、)、[、]四种字符中的若干种构成的字符串。

输入格式
输入仅一行，为字符串 BE。

输出格式
输出仅一个整数，表示增加的最少字符数。

数据范围
对于所有输入字符串，其长度小于100。

输入样例：
[])
输出样例：
1

思路：

本题是acwing.1222. 密码脱落的例题，也是考察区间DP。（与POJ2955类似）

与密码脱落这题不同的地方在于A、B乘起来的结果是GBE，类似于密码脱落和石子合并两题的结合。

若括号序列是回文串，那么一定是合法的。但是该题新加了一个条件即()[]这样并列的括号也是合法的。

这里的定义2中的GBE也就是一个回文序列（如[()()]），定义2中的GBE是一个并列括号序列（如()[]）。

注意一下：定义2中的GBE和回文序列还是有一点区别的，单个符号可以是回文序列，但不满足GBE。

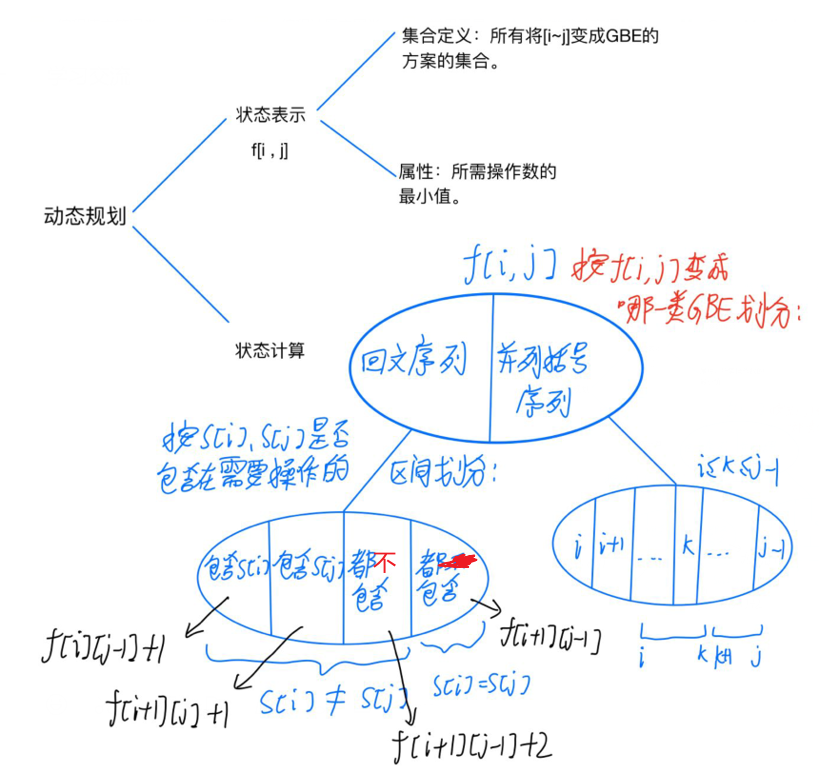
算法1：y式DP分析法。

image-20210628210930813

按s[i]、s[j]是否包含在需要操作的区间划分，也就是说s[i]、s[j]是否包含在进行操作使之变成GBE的区间中。

都不包含这类情况显然是包含在前两种情况中，所以可以不考虑。

注意整个集合划分的特点：先进行回文序列的划分，执行计算，然后再进行并列括号序列的划分，这两步是先后顺序，不是并列的关系。（和其他大部分集合划分的一个不同点）

并列括号序列中，k从i开始取，到j-1结束，因为(i,i)这种序列也需要操作。

时间复杂度：O(n^3)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 105;
int INF = 0x3f3f3f3f;
int dp[N][N];
char s[N];

bool check(char l,char r){// 检查是否满足s[i] == s[j]
    if (l == '(' && r == ')') return true;
    if (l == '[' && r == ']') return true;
    return false;
}
int main(){
    scanf("%s",s);
    int n = strlen(s);
    
    for (int len = 1;len <= n;len++)
        for (int i = 0;i + len - 1 < n;i++){
            int j = i + len - 1;
            if (len == 1) dp[i][j] = 1;
            else{// len >= 2的情况，至少2个字符
                dp[i][j] = INF;// 求min，初始化INF，排除不合法状态
                if (check(s[i],s[j])) dp[i][j] = dp[i+1][j-1];// 集合1情况4
                dp[i][j] = min(dp[i][j], min(dp[i][j-1],dp[i+1][j]) + 1);// 集合1情况23
                for (int k = i;k <= j-1;k++){// 集合2
                    dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j]);
                }
            }
        }
    printf("%d\n",dp[0][n-1]);
    return 0;
}

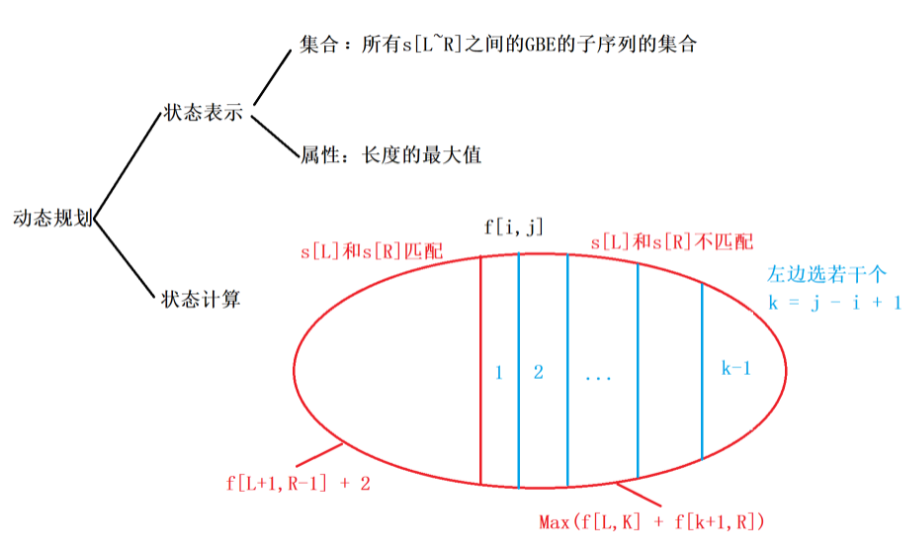
算法2：另一种DP分析法。

参考题解：https://www.acwing.com/solution/content/8845/。（和POJ2955做法类似）

从当前BE变成GBE需要添加最少字符的数量 等价于 当前BE变成最大的GBE需要去掉字符的数量
即至少添加最少字符 等价于 总数量 - 最大GBE子序列的长度。

注意：这题和密码脱落也有些不同，GBE有回文的性质 或者 有另外一种性质，例如[]() , ([])均是GBE，因此需要对s[L] 和 s[R]不匹配的情况需要进一步划分，划分方式和石子合并类似。

image-20210628220235949

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 105;
int INF = 0x3f3f3f3f;
int dp[N][N];
char s[N];

bool check(char l,char r){// 检查是否满足s[i] == s[j]
    if (l == '(' && r == ')') return true;
    if (l == '[' && r == ']') return true;
    return false;
}
int main(){
    scanf("%s",s);
    int n = strlen(s);
    
    for (int len = 1;len <= n;len++)
        for (int i = 0;i + len - 1 < n;i++){
            int j = i + len - 1;
            // if (len == 1) dp[i][j] = 0;可省略
            if (check(s[i],s[j])) dp[i][j] = dp[i+1][j-1] + 2;// 集合1
            
            for (int k = i;k <= j-1;k++){
                dp[i][j] = max(dp[i][j],dp[i][k] + dp[k+1][j]);// 集合2
            }
        }
    printf("%d\n",n - dp[0][n-1]);
    return 0;
}
坚持原创技术分享，您的支持将鼓励我继续创作！