grant's Blog

记录生活中的点点滴滴

蓝桥杯学习总结（二二）

发表于 更新于 分类于 ，   阅读次数： Valine：
本文字数： 4.2k 阅读时长 ≈ 4 分钟

六 贪心

贪心问题没有普遍统一的模板，跳跃性很强，结论证明往往很难。

做法：1.找以往做过的相似的题目 2.不会的只能靠猜了

贪心是求解一类最优化问题的方法，考虑当前状态下局部最优的策略，来使全局结果达到最优。

贪心的证明往往比贪心更难。

代码随想录：贪心专题文章，题目数量多，总结全面。LeetCode101贪心算法专题。

要证明贪心策略的正确性常会用到反证法，找一找是否有反例，还有一种就是数学归纳法。

做题时没必要非得证明出来，能AC就能成功。

1 acwing.1055. 股票买卖 II（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
给定一个长度为 N 的数组，数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

输入格式
第一行包含整数 N，表示数组长度。
第二行包含 N 个不大于 10000 的正整数，表示完整的数组。

输出格式
输出一个整数，表示最大利润。

数据范围
1≤N≤10^5
输入样例1：
6
7 1 5 3 6 4
输出样例1：
7
输入样例2：
5
1 2 3 4 5
输出样例2：
4
输入样例3：
5
7 6 4 3 1
输出样例3：
0
样例解释
样例1：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。共得利润 4+3 = 7。

样例2：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

样例3：在这种情况下, 不进行任何交易, 所以最大利润为 0。

思路：

根据数据范围，时间复杂度应该控制为：O(n)或者O(n*logn)。

交易策略：对于数组的相邻两天，只要后一天比前一天价格高，就进行一次交易。

性质：任意交易天数跨度大于1的交易，必然可以分解为多个交易天数等于1的交易。

代码：

时间复杂度：O(n).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int N  = 1e5+10;
int n;
int price[N];

int main(){
    scanf("%d",&n);
    for (int i = 0;i < n;i ++) scanf("%d",&price[i]);
    int res = 0;
    for (int i = 0;i < n-1;i++){
        int dt = price[i+1] - price[i];
        if (dt > 0) res += dt;
    }
    printf("%d\n",res);
    return 0;
}

2 acwing.104. 货仓选址

《算法竞赛进阶指南》, 模板题

本题在寒假每日一题中出现过。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
在一条数轴上有 N 家商店，它们的坐标分别为 A1∼AN。
现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。
为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

输入格式
第一行输入整数 N。
第二行 N 个整数 A1∼AN。

输出格式
输出一个整数，表示距离之和的最小值。

数据范围
1≤N≤100000,
0≤Ai≤40000
输入样例：
4
6 2 9 1
输出样例：
12

思路：

从直觉上看，我们不妨猜货仓应该建在所有商店的中间位置。

这很容易证明，如果建在两个商店之外，距离一定比在中间大。

从2个、3个商店，手动模拟一下，很容易发现上述规律，应该建在中位数这个位置。

出题人往往根据已有的数学模型，包装成一个题目，用贪心求解。

严格数学证明：

image-20210530172414373

问题核心在于分组求绝对值之和最大值。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
int n;
int a[N];

int main(){
    scanf("%d",&n);
    for (int i = 0;i < n;i++) scanf("%d",&a[i]);
    sort(a,a+n);
    
    int c = a[n/2];// 求中位数
    LL res = 0;// 用LL来存
    for (int i = 0;i < n;i++) res += abs(a[i] - c);// 求距离
    printf("%lld",res);
    
    return 0;
}

3 acwing.122. 糖果传递（困难）

《算法竞赛进阶指南》,微软面试题 , HAOI2008，有难度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
有 n 个小朋友坐成一圈，每人有 a[i] 个糖果。
每人只能给左右两人传递糖果。
每人每次传递一个糖果代价为 1。
求使所有人获得均等糖果的最小代价。

输入格式
第一行输入一个正整数 n，表示小朋友的个数。
接下来 n 行，每行一个整数 a[i]，表示第 i 个小朋友初始得到的糖果的颗数。

输出格式
输出一个整数，表示最小代价。

数据范围
1≤n≤1000000,
0≤a[i]≤2×10^9,
数据保证一定有解。

输入样例：
4
1
2
5
4
输出样例：
4

思路：数学演算

image-20210602151746775

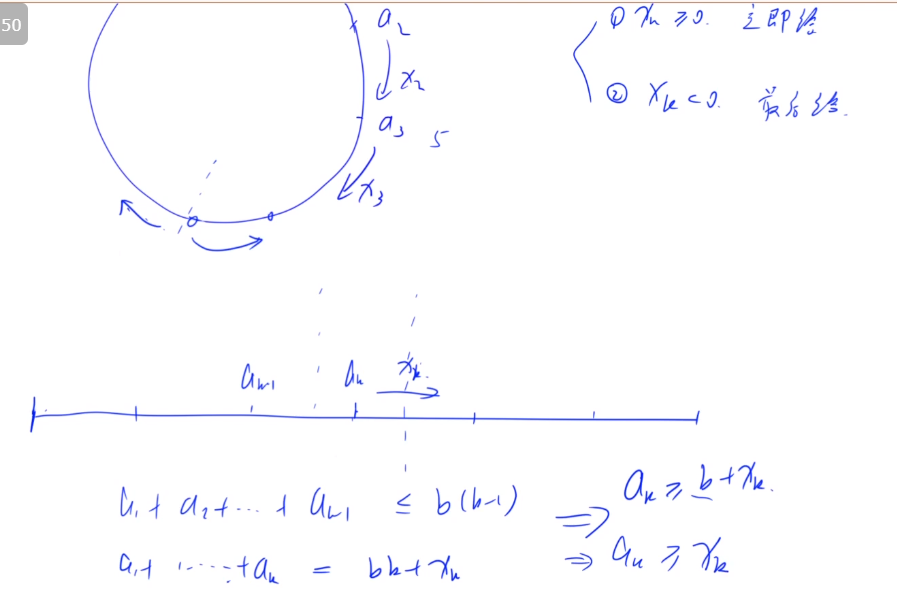
将所有量进行数学化计算，构建数学模型，最终结果就是极小化红色标注的绝对值不等式，然后就可以直接套用上一题货仓选

址的做法。（$x_1$等表示从$a_1$传递到$a_2$的糖果数量，可正可负，如果是负数表示是反向传递的）

下一步，要证明方案是否一定存在。（如果只想AC可以不看证明）

比如，当a1=3时，x3=5，方案就不成立，因为给出的糖果不可能比已有的还多。

首先可以证明：

所有$x_i(i=1,2,…,n)$同时大于0不成立。假设所有$x_i$大于0，那么可以让所有$x_i$都减去最小的$x_i$，使得每个

人得到的糖果数量是一样的效果，因为相互抵消了，这是就有部分$x_i$等于0，部分大于0，所以不成立。

同理可以证明所有$x_i(i=1,2,…,n)$同时小于0也不成立。

由上述结论可知：存在部分$x_i>=0$，部分<0。

一定存在至少一个分界点$a_m$满足左边>=0，右边<0。也就是说这个人一定往两边传递糖果。

那我们可以从分界点处把环变成一条直线。

image-20210603084728611

image-20210603085513979

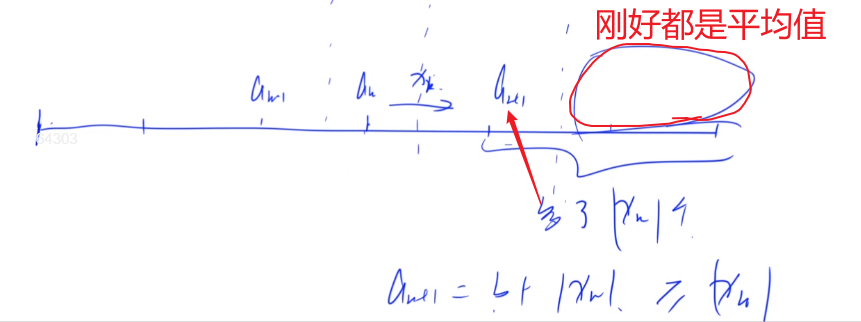
对于每一个$x_k$，分成两种情况，当$x_k>=0$时，糖果立即传递给右边；当$x_k<0$时，先不给。

我们先考虑糖果从左往右传递的情况，可以得到上上图的两个式子。

第一个式子：当$x_{k-1}>=0$时，$a_1$到$a_{k-1}$的糖果数小于（我觉得是等于）平均值。

然后再根据第二个式子，就能得到$a_k >= x_k$，得证。

从右往左传递糖果时，dfs回溯。

image-20210603093751143

以上证明实在看不懂可以略过。（不影响AC）

参考题解：https://www.acwing.com/solution/content/5531/

image-20210603094531778

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// y总题解
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1000010;
LL c[N];// 避免爆int都用LL存
LL s[N];
int n;
int main(){
    scanf("%d",&n);
    for (int i = 1;i <= n;i++){
        scanf("%lld",&s[i]);
        s[i] += s[i-1]; // 求前缀和
    }
    LL  ave = s[n]/n;
    int k = 0;
    for (int i = 1;i < n;i++){// 注意边界，计算c[0]到c[n-2]
        c[k++] = i*ave - s[i];
    }
    c[k++] = 0;// 再计算c[n-1]

    sort(c,c+k);// 题解1，排序，O(n*logn)，比题解2慢2倍左右
    LL m = c[k/2];
    //nth_element(c,c+k/2,c+k); 题解2，O(n)，比较快
    LL res = 0;
    for (int i = 0;i < n;i++) res += abs(c[i] - m);// 注意边界
    //for (int i = 0;i < n;i++) res += abs(c[i] - c[k/2]);
    printf("%lld",res);
    return 0;
}

补充：

快速选择函数nth_element(数组初位置，寻找元素，数组末位置)（STL）

也可以自己实现，利用快排。

C++的STL库中的nth_element()方法，默认是求区间第k小的（划重点）。

举个栗子求第3小，对于 a[9]={4,7,6,9,1,8,2,3,5};

nth_element(a,a+2,a+9)，将下标为2，也就是第3个数放在正确的位置，求的是第3小的数a[2]。（下标从零开始）

寒假每日一题入门题（一）中介绍过两种题解。

1.sort，时间复杂度：O(n*logn) 2.nth_element，时间复杂度：O(n)

坚持原创技术分享，您的支持将鼓励我继续创作！