1.第二讲线性表

非常全面！

1.1线性表

将具有线性关系的数据存储到计算机中所使用的存储结构称为线性表。
对于线性表中的数据来说，位于当前数据之前的数据统称为“前趋元素”，前边紧挨着的数据称为“直接前趋”；同样，后边的数据统称为“后继元素”，后边紧挨着的数据称为“直接后继”。
线性表的分类
(1) 数据元素在内存中集中存储，采用顺序表示结构，简称“顺序存储”；
```
 例如：数组
```
(2) 数据元素在内存中分散存储，采用链式表示结构，简称“链式存储”。
```
 例如：单链表、双链表、循环单（双）链表
```
不同实现方式的时间复杂度（不要硬背结论、要从实现方式入手分情况讨论，下述为特定情况下的时间复杂度）
(1) 数组：随机索引O(1)、插入O(n)、删除O(n)
(2) 单链表：查找某一元素O(n)、插入O(1)、删除O(n)，删除当前节点需要找到它的前驱
(3) 双链表：查找某一元素O(n)、插入O(1)、删除O(1)

简单回顾一下单链表：（不要背代码！！！理解记忆！！！）

头插法：新节点插入在链表的最前端；尾插法：新节点插入在链表的最末端。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

struct Node{
    int val;
    Node* next;

    // Node构造函数，next初始化为NULL
    Node():next(NULL) {}
    Node(int _val):val(_val),next(NULL){}
};

void print(Node* head){ // 遍历打印单链表
    for (auto p = head->next; p;){
        cout << p->val;
        p = p->next;
        if (p != NULL)  cout << " --> ";
    }
    cout << endl;
}

void headInsert(Node* head,Node* tail,int n){ // 头插法
    auto node = new Node(n);

    node->next = head->next;
    head->next = node;
}

void tailInsert(Node* tail,int n){ // 尾插法
    auto node = new Node(n);
    
    tail->next->next = node;
    tail->next = node;
}

bool ListDelete(Node* head,int n){ // 删除单链表中第n个位置的元素，head指向的是第1个位置
    bool flag = false;
    if (n == 1){
        flag = true;
        head->next = head->next->next;
        return flag;
    }

    n --;
    for (auto p = head->next; p; n --){
        if (n == 1){
            p->next = p->next->next;
            flag = true;
            return flag;
        }
        p = p->next;
    }
    return flag;
}

int main(){
    auto head = new Node();
    auto node = new Node(1);
    head->next = node; // 头指针

    auto tail = new Node();
    tail->next = node; // 尾指针
    
    headInsert(head,tail,2);
    print(head);
    cout << head->next->val << " " << tail->next->val << endl;
    tailInsert(tail,3);
    print(head);
    cout << head->next->val << " " << tail->next->val << endl;
    headInsert(head,tail,4);
    print(head);
    cout << head->next->val << " " << tail->next->val << endl;
    tailInsert(tail,5);
    print(head);
    cout << head->next->val << " " << tail->next->val << endl;
    if (ListDelete(head,1)){
        print(head);
        cout << head->next->val << " " << tail->next->val << endl;
    }
    if (ListDelete(head,5)){
        print(head);
        cout << head->next->val << " " << tail->next->val << endl;
    }
    return 0;
}

简单回顾一下双链表：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

struct Node{
    int val;
    Node *prev,*next;

    // Node构造函数，next初始化为NULL
    Node():prev(NULL),next(NULL) {}
    Node(int _val):val(_val),prev(NULL),next(NULL){}
};

void print(Node* head,Node* tail){ // 遍历打印单链表
    for (auto p = head->next; p;){
        if (p != tail) cout << p->val;
        p = p->next;
        if (p != tail && p != NULL)  cout << " --> ";
    }
    cout << endl;
}

int main(){
    Node *head = new Node(),*tail = new Node();
    head->next = tail,tail->prev = head; // 定义左右哨兵

    // 头插法
    auto a = new Node(1);
    a->next = head->next,a->prev = head;
    head->next->prev = a,head->next = a;
    print(head,tail);

    auto b = new Node(2);
    b->next = head->next,b->prev = head;
    head->next->prev = b,head->next = b;
    print(head,tail);

    // 删除b结点
    b->prev->next = b->next;
    b->next->prev = b->prev;

    return 0;
}

理解了做题就很容易。

注：408中的单、双链表的定义最好参考王道的图，不会有像上面代码中左、右哨兵的写法。

三道大题

链表题最好先在纸上画图，然后对照着实现每一步操作的代码。

2012-42：

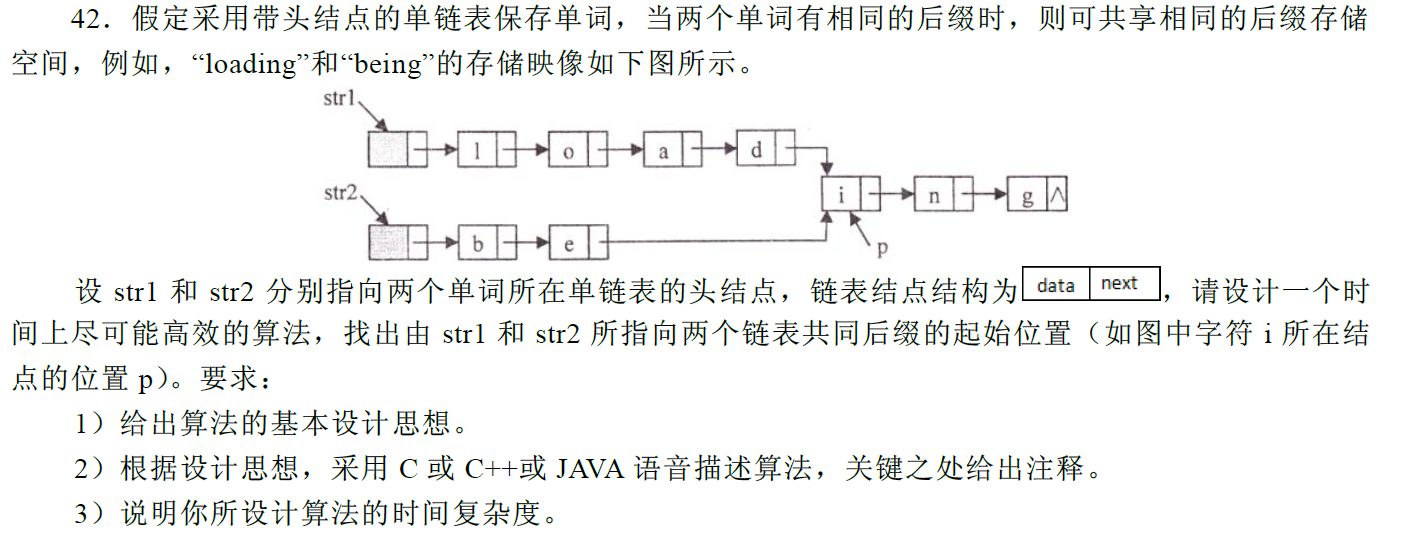
66. 两个链表的第一个公共结点

输入两个链表，找出它们的第一个公共结点。

当不存在公共节点时，返回空节点。

样例

给出两个链表如下所示：
A：        a1 → a2
                   ↘
                     c1 → c2 → c3
                   ↗            
B:     b1 → b2 → b3

输出第一个公共节点c1

在《C++竞赛语法总结（七）》中提到过本题。

这里细致讲解一下，采用双指针算法。

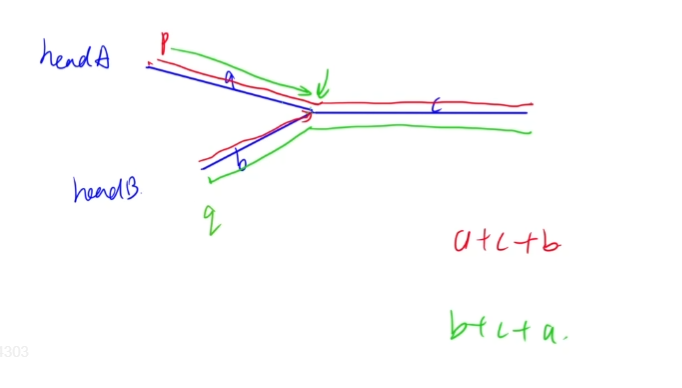
定义两个指针分别叫做headA和headB。

headA从链表A的头出发，走过的路径是a-->c-->b；

headB从链表B的头出发，走过的路径是b-->c-->a。

两个指针走过的总路线长度是一样的，所以它们必定会相遇。

当a == b时，两个指针每次一起向前移动一位，所以一定在交点相遇；

当a != b时，不妨设a > b，那么a+c > b+c，所以在headB开始走a路段之前它们都不会相遇，两条路径的终点都是交点，也就是说在交点之前都不会相遇，最终的相遇点就是交点。

如果两个链表不相交，那么两个指针就会分别走到对方链表的末尾结束。

以上论证了双指针算法的正确性。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *findFirstCommonNode(ListNode *headA, ListNode *headB) {
        ListNode *p = headA,*q = headB;
        while (p != q){ // 直到两个指针相遇或者同时走到NULL返回结果
            p = p ? p->next : headB; // 如果指针走到链表尾，就从另一个链表头开始走
            q = q ? q->next : headA;
        }
        return p;
    }
};

2015-41：

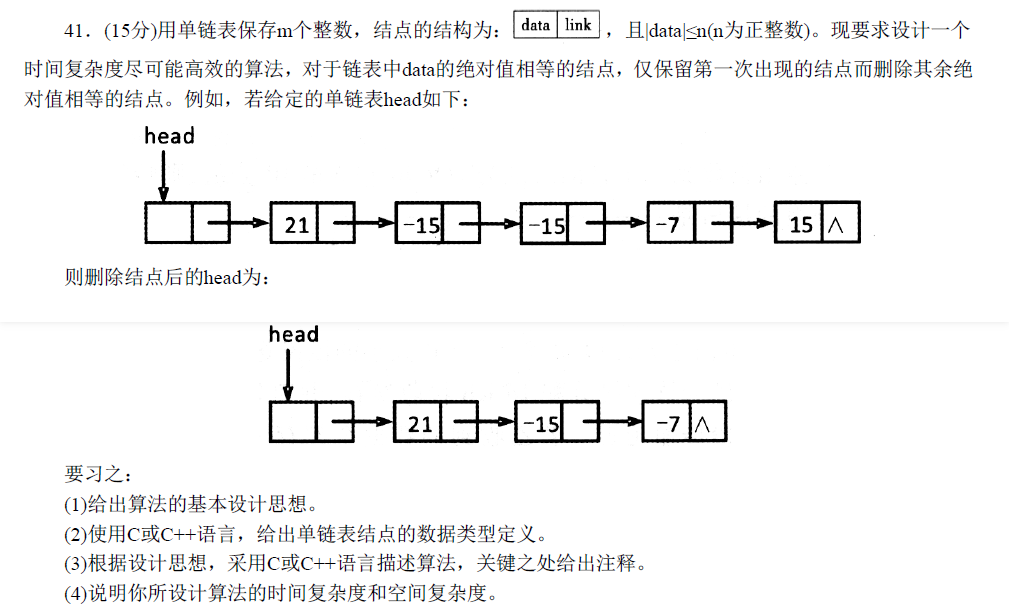
核心问题就是如何判断一个数的绝对值是否出现过。

我首先想到的是哈希表，但答案要求没有这么高，开一个bool[n]数组就行。

可以给单链表设置一个头节点（如图），从头节点开始遍历链表，判断是否需要删除下一个节点。这是由单链表的特性所决定的，只有知道上一个节点才可以删除当前节点。

3756. 筛选链表

一个单链表中有 m 个结点，每个结点上的元素的绝对值不超过 n。
现在，对于链表中元素的绝对值相等的结点，仅保留第一次出现的结点而删除其余绝对值相等的结点。

请输出筛选后的新链表。
例如，单链表 21 -> -15 -> -15 -> -7 -> 15，在进行筛选和删除后，变为 21 -> -15 -> -7。

输入样例：
输入：21->-15->-15->-7->15
输出：21->-15->-7
数据范围
1≤m≤1000,
1≤n≤10000

遍历链表的时候，用一个数组标记是否已经出现过该元素。出现就在对应的位置true，否则false。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:   // 注意：本题的head实际是首节点，也就是说它存了值
    ListNode* filterList(ListNode* head) {
        bool st[10000] = {0}; // 全部初始化为0，避免随机值
        st[abs(head->val)] = true; // 首节点存放的值是第一个
        // p指针遍历，判断它的下一个节点是否要删除
        for (auto p = head;p->next;){ // p指针从首节点开始遍历，直到倒数第2个节点
            int x = abs(p->next->val);
            if (st[x]){ // 如果绝对值重复，就需要删除下一个节点，直到没有重复p再往前走
                auto q = p->next;
                p->next = q->next;
                delete q; // 释放内存
            }else{
                st[x] = true; // 绝对值不重复，p往前走
                p = p->next;
            }
        }
        return head;
    }
};

引入真正头节点（不存储信息）的题解： https://www.acwing.com/solution/content/57458/。

类似的做法还可以参考《C++竞赛语法总结（七）》的删除链表中重复元素。

2019-41：

3757. 重排链表（中等难度）

一个包含 n 个元素的线性链表 L=(a1,a2,…,an−2,an−1,an)。

现在要对其中的结点进行重新排序，得到一个新链表 L′=(a1,an,a2,an−1,a3,an−2…)
样例1：
输入：1->2->3->4

输出：1->4->2->3
样例2：
输入：1->2->3->4->5

输出：1->5->2->4->3
数据范围
1≤n≤1000,
1≤ai≤10000

交替重排链表，是反转链表和合并链表的结合版。

反转链表参考《C++竞赛语法总结（六）》的反转链表。

注意题目要求空间复杂度为O(1)，不能开辟新的链表只能操作原链表。

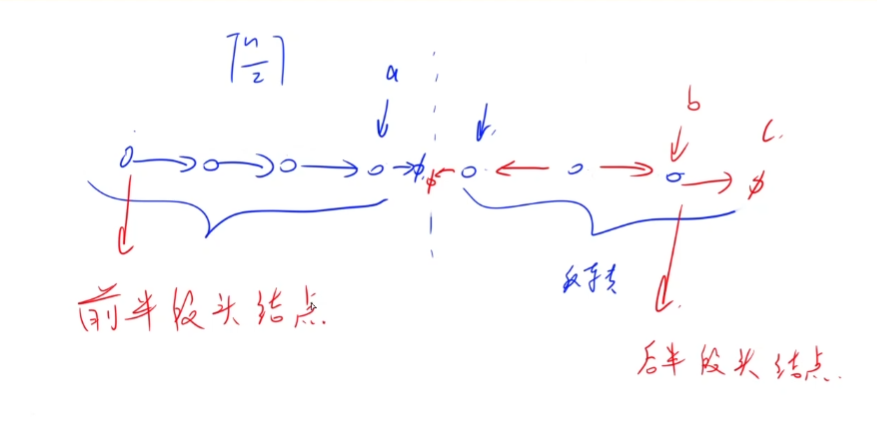
第一步，将链表分成两部分。左半部分的元素个数是$\lceil \frac n 2 \rceil$,右半部分的元素个数是$n- \lceil \frac n 2 \rceil$。

为什么是上取整？按照新链表的排列顺序，如果是奇数个元素，最后一个元素会从左边取。

图示：找到两边的边界点，分别记为a，b。

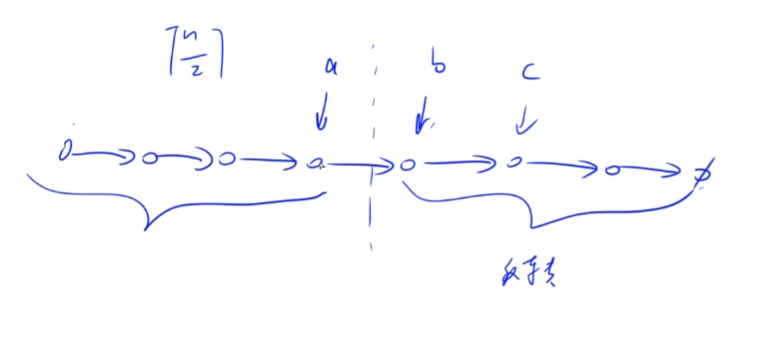
操作完两部分链表后：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    void rearrangedList(ListNode* head) {
        if (!head->next) return;
        int n = 0;
        for (auto p = head; p; p = p->next) n ++; // 求链表的节点个数n
        int left = (n+1) >> 1; // (n+1)/2 等于 n/2上取整
        
        auto a = head; // 左边有left个元素需要移动left-1次
        for (int i = 0;i < left - 1;i ++) a = a->next;
        auto b = a->next,c = b->next;
        
        a->next = b->next = NULL;
        while (c){ // 反转右边的链表
            auto t = c->next;
            c->next = b;
            b = c,c = t;
        } // 反转完后：b指向右边的头，c指向NULL
        
        // 交替合并链表
        for (auto p = head,q = b;q;){ // 左边数量 >= 右边数量
            auto t1 = p->next,t2 = q->next;
            p->next = q;
            q->next = t1;
            
            p = t1;
            q = t2;
        }
    }
};

注意：真正理解链表结构体的赋值（a = b）的原理：

https://blog.csdn.net/qianggea11/article/details/90695101。

grant's Blog

考研算法辅导课笔记（二）

1.第二讲线性表

1.0数据结构课本相关代码实现

1.1线性表

三道大题

2012-42：

66. 两个链表的第一个公共结点

2015-41：

3756. 筛选链表

2019-41：

3757. 重排链表（中等难度）

1.第二讲 线性表

1.0数据结构课本相关代码实现

1.1线性表

三道大题

2012-42：

66. 两个链表的第一个公共结点

2015-41：

3756. 筛选链表

2019-41：

3757. 重排链表（中等难度）

1.第二讲线性表