grant's Blog

记录生活中的点点滴滴

蓝桥杯学习总结（二十）

发表于 更新于 分类于 ，   阅读次数： Valine：
本文字数： 6.6k 阅读时长 ≈ 6 分钟

4.习题

4.1 acwing.1240. 完全二叉树的权值

第十届蓝桥杯省赛C++A/B组,第十届蓝桥杯省赛JAVAA组

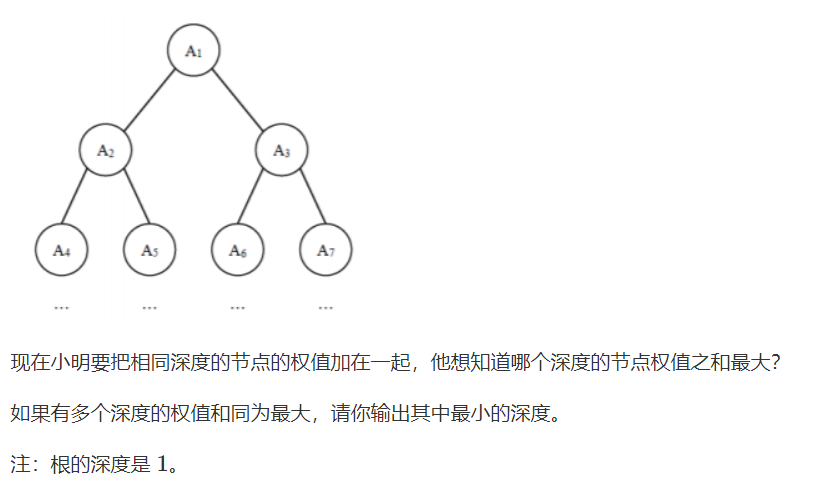
给定一棵包含 NN 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是

A1,A2,⋅⋅⋅ANA1,A2,···AN，如下图所示：

image-20210527154520270

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
输入格式
第一行包含一个整数 N。
第二行包含 N 个整数 A1,A2,⋅⋅⋅AN。

输出格式
输出一个整数代表答案。

数据范围
1≤N≤105,
−105≤Ai≤105
输入样例：
7
1 6 5 4 3 2 1
输出样例：
2

思路：（比较简单）

双指针算法。时间复杂度：O(n)。

把每个数遍历一次，所以是O(n)。

对层数进行循环，分别求权值之和，更新最大值。

image-20210527212154148

注意爆int。

满二叉树的深度为log(1e5) 最多可以有 1 << (log(1e5)) - 1个元素 大概是2^15 ~ 2^16 ，再乘以一个 1e5 所以就爆了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5+10;
const int INF = 0x3f3f3f3f;// 无穷大
int n;
int t[N];
int main(){
    scanf("%d",&n);
    for (int i = 1;i <= n;i++) scanf("%d",&t[i]);

    LL max = -INF;
    int depth = 0;
    for (int i = 1, d = 1;i <= n;i *= 2,d++){// i不能从0开始，从1开始才有*2的规律
        LL s = 0;
        for (int j = i;j < i + (1 << d-1) && j <= n;j++) s += t[j];
        if (s > max){
            max = s;
            depth = d;
        }
    }
    printf("%d\n",depth);
    return 0;
}

4.2 acwing.1096. 地牢大师

《信息学奥赛一本通》 , POJ 2251

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
你现在被困在一个三维地牢中，需要找到最快脱离的出路！
地牢由若干个单位立方体组成，其中部分不含岩石障碍可以直接通过，部分包含岩石障碍无法通过。
向北，向南，向东，向西，向上或向下移动一个单元距离均需要一分钟。
你不能沿对角线移动，迷宫边界都是坚硬的岩石，你不能走出边界范围。
请问，你有可能逃脱吗？
如果可以，需要多长时间？

输入格式
输入包含多组测试数据。
每组数据第一行包含三个整数 L,R,C 分别表示地牢层数，以及每一层地牢的行数和列数。
接下来是 L 个 R 行 C 列的字符矩阵，用来表示每一层地牢的具体状况。
每个字符用来描述一个地牢单元的具体状况。
其中, 充满岩石障碍的单元格用”#”表示，不含障碍的空单元格用”.”表示，你的起始位置用”S”表示，终点用”E”表示。
每一个字符矩阵后面都会包含一个空行。
当输入一行为”0 0 0”时，表示输入终止。

输出格式
每组数据输出一个结果，每个结果占一行。
如果能够逃脱地牢，则输出”Escaped in x minute(s).”，其中X为逃脱所需最短时间。
如果不能逃脱地牢，则输出”Trapped!”。

数据范围
1≤L,R,C≤100
输入样例：
3 4 5
S....
.###.
.##..
###.#

#####
#####
##.##
##...

#####
#####
#.###
####E

1 3 3
S##
#E#
###

0 0 0
输出样例：
Escaped in 11 minute(s).
Trapped!

思路：

这是一个三维的迷宫问题。

根据数据范围：迷宫最多是10^6，所以时间复杂度应当控制为：O(n)。

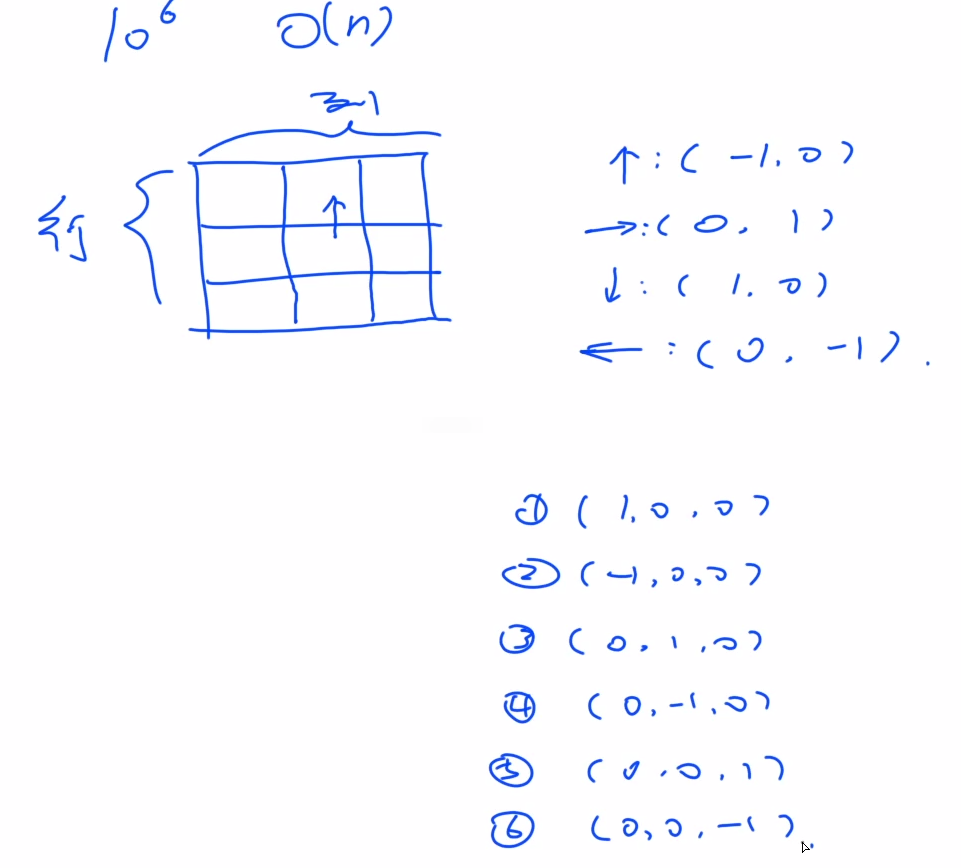
做法：二维BFS扩展成三维BFS。

二维与三维坐标偏移对比：

image-20210528202135319

代码：队列，队尾入队，队头出队。

本题用数组实现BFS，用队列queue也行，效率更低一点。可以当作模板记忆了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
// y总代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 101;
struct Point{
    int x,y,z;// 对应三个坐标维度
};

int dx[] = {1,-1,0,0,0,0};// 6个方向
int dy[] = {0,0,1,-1,0,0};
int dz[] = {0,0,0,0,1,-1};
int L,R,C;
char g[N][N][N];
int dist[N][N][N];// 距离与判重数组
Point q[N*N*N];// 用数组代替队列

int bfs(Point S,Point E){
    int hh = 0,tt = 0;
    q[0] = S;// 入队
    memset(dist,-1,sizeof dist);
    dist[S.x][S.y][S.z] = 0;
    while (hh <= tt){// 队尾没碰到队头说明队列非空，必须是<=
        auto t = q[hh++];// hh相当于队尾指针，元素插入队尾
        for (int i = 0;i < 6;i++){
            int x = t.x + dx[i],y = t.y + dy[i],z = t.z + dz[i];
            // 不能出界
            if ( x < 0 || x >= L || y < 0 || y >= R || z < 0 || z >= C) continue;
            // 判断是否走过
            if (dist[x][y][z] != -1) continue;
            // 判断障碍物
            if (g[x][y][z] == '#') continue;

            dist[x][y][z] = dist[t.x][t.y][t.z] + 1;
            if (g[x][y][z] == 'E') return dist[x][y][z];

            q[++tt] = {x,y,z};// tt相当于队头指针，有hh处插入的元素拓展的元素插入队尾
        }
    }
    return -1;
}
int main(){
    Point start,end;
    while (scanf("%d %d %d",&L,&R,&C),L && R && C){
        for (int i = 0;i < L;i++)
            for (int j = 0;j < R;j++){
                scanf("%s",g[i][j]);
                for (int k = 0;k < C;k++){
                    if (g[i][j][k] == 'S') start = {i,j,k};
                }
            }
        int res = bfs(start,end);
        if (res == -1) puts("Trapped!");
        else printf("Escaped in %d minute(s).\n",res);
    }
    return 0;
}

4.3 acwing.1233. 全球变暖

第九届蓝桥杯省赛C++A/B组,第九届蓝桥杯省赛JAVAA/B组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
你有一张某海域 N×N 像素的照片，”.”表示海洋、”#”表示陆地，如下所示：
.......
.##....
.##....
....##.
..####.
...###.
.......
其中”上下左右”四个方向上连在一起的一片陆地组成一座岛屿，例如上图就有 2 座岛屿。
由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。
具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋)，它就会被淹没。
例如上图中的海域未来会变成如下样子：
.......
.......
.......
.......
....#..
.......
.......
请你计算：依照科学家的预测，照片中有多少岛屿会被完全淹没。

输入格式
第一行包含一个整数N。
以下 N 行 N 列，包含一个由字符”#”和”.”构成的 N×N 字符矩阵，代表一张海域照片，”#”表示陆地，”.”表示海洋。
照片保证第 1 行、第 1 列、第 N 行、第 N 列的像素都是海洋。

输出格式
一个整数表示答案。

数据范围
1≤N≤1000
输入样例1：
7
.......
.##....
.##....
....##.
..####.
...###.
.......
输出样例1：
1
输入样例2：
9
.........
.##.##...
.#####...
.##.##...
.........
.##.#....
.#.###...
.#..#....
.........
输出样例2：
1

思路：

这题也是考察Flood Fill（洪水灌溉）算法。

根据数据范围推断时间复杂度要控制为O(n)。

十九讲的红与黑求的是一个连通块的大小，而这题求的是连通块的个数，有多个。

先统计一共有多少连通块，再计算被淹没的连通块有多少个。

如何判断岛屿是否被淹没？

我们可以开两个变量total和bound，分别表示总像素个数和边界像素个数，如果total == bound，说明淹

没。

total怎么算？每拓展一个像素，total+1；

bound怎么算？拓展的像素四个方向有海，bound+1.

代码1：BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
const int N = 1e3+5;

char g[N][N];
PII q[N*N];// bfs数组
bool st[N][N];// 判重数组
int n;
int dx[] = {1,-1,0,0},dy[] = {0,0,1,-1};

void bfs(int x,int y,int &total,int &bound){// 注意total和bound必须是引用传递
    int hh = 0,tt = 0;
    q[0] = {x,y};
    st[x][y] = true;
    while (hh <= tt){
        auto t = q[hh++];
        total++;
        bool is_bound = false;
        for (int i = 0;i < 4;i++){
            int a = t.x + dx[i],b = t.y + dy[i];
            if (a < 0 || a >= n || b < 0 || b >= n) continue;
            if (st[a][b]) continue;
            if (g[a][b] == '.'){
                is_bound = true;
                continue;
            }
            q[++tt] = {a,b};
            st[a][b] = true;
        }
        if (is_bound) bound++;
    }

}

int main(){
    scanf("%d",&n);
    for (int i = 0;i < n;i++) scanf("%s",g[i]);

    int cnt = 0;
    for (int i = 0;i < n;i++)
        for (int j = 0;j < n;j++){
            if(!st[i][j] && g[i][j] == '#'){// 对每个陆地像素搜索计算连通块个数
                int total = 0,bound = 0;
                bfs(i,j,total,bound);
                if (bound == total) cnt++;
            }
        }
    printf("%d\n",cnt);
    return 0;
}

代码2：DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;

int n;
char a[1010][1010]; //地图
int vis[1010][1010]={0};  //标记是否搜过
int d[4][2] = {{0,1}, {0,-1}, {1,0}, {-1,0}}; //四个方向
int flag;  //用于标记这个岛中是否被完全淹没
void dfs(int x, int y){
    vis[x][y] = 1;      //标记这个'#'被搜过。注意为什么可以放在这里
    if(a[x][y+1]=='#' && a[x][y-1]=='#' && a[x+1][y]=='#' && a[x-1][y]=='#')
        flag = 1;       //上下左右都是陆地，不会淹没
    for(int i = 0; i < 4; i++){ //继续DFS周围的陆地
        int nx = x + d[i][0], ny = y + d[i][1];
      //if(nx>=1 && nx<=n && ny>=1 && ny<=n && vis[nx][ny]==0 && a[nx][ny]=='#') //题目说边上都是水，所以不用这么写了
        if(vis[nx][ny]==0 && a[nx][ny]=='#') //继续DFS未搜过的陆地，目的是标记它们
            dfs(nx,ny);
    }
}

int main(){
    cin >> n;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            cin >> a[i][j];
    int ans = 0 ;
    for(int i = 1; i <= n; i++)  //DFS所有像素点
        for(int j = 1; j <= n; j++)
            if(a[i][j]=='#' && vis[i][j]==0){
                flag = 0;
                dfs(i,j);
                if(flag == 0)  //这个岛全部被淹
                    ans++;     //统计岛的数量
            }
    cout<<ans<<endl;
    return 0;
}


作者：Ooooooooooops
链接：https://www.acwing.com/solution/content/16140/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

DFS：地图从1开始计算，外面多了一圈，就不用单独处理越界情况。

坚持原创技术分享，您的支持将鼓励我继续创作！