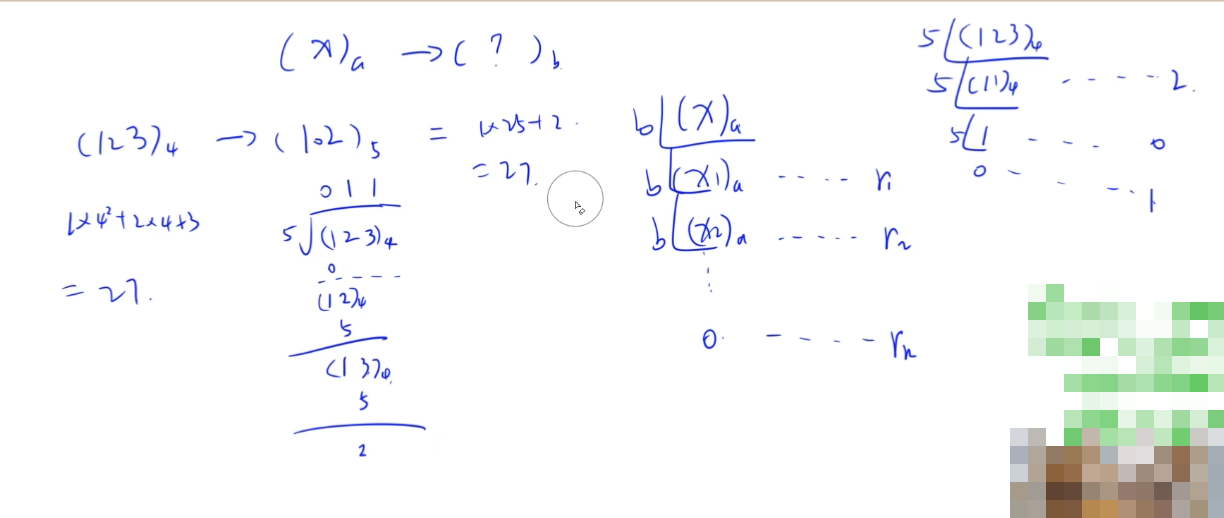1.关于408数据结构
y总原话:考研DS,笔试和上机是两回事,关系不大。笔试考背诵,上机是敲代码(正儿八经的算法)。这两块东西需要分开独立复习。(PS:过了初试才有上机呀~)
推荐配合王道的数据结构掌握考试八股知识,看这个巩固笔试机试水平。
笔试整体难度不大,但细节很多,需要记忆。
像这种八股文,学第一遍挺简单,但是容易忘记,需要反复记忆。
推荐两个408算法题练习清单,清单。
这里是牛客网的408考研专场: https://www.nowcoder.com/kaoyan.
408算法考纲:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
| 考纲:
一、线性表
(一)线性表的定义和基本操作
(二)线性表的实现
1. 顺序存储
2. 链式存储
3. 线性表的应用
二、栈、队列和数组
(一)栈和队列的基本概念
(二)栈和队列的顺序存储结构
(三)栈和队列的链式存储结构
(四)栈和队列的应用
(五)特殊矩阵的存储和压缩
三、树与二叉树
(一)树的基本概念
(二)二叉树
1. 二叉树的定义及其主要特征
2. 二叉树的顺序存储结构和链式存储结构
3. 二叉树的遍历
4. 线索二叉树的基本概念和构造
(三)树、森林
1. 树的存储结构
2. 森林与二叉树的转换
3. 树和森林的遍历
(四)树与二叉树的应用
1. 二叉排序树
2. 平衡二叉树
3. 哈夫曼(Huffman)树的哈弗曼编码
四、图
(一)图的基本概念
(二)图的存储及基本操作
1. 邻接矩阵法
2. 邻接表法
3. 邻接多重表、十字链表
(三)图的遍历
1. 深度优先搜索
2. 广度优先搜索
(四)图的基本应用
1. 最小(代价)生成树
2. 最短路径
3. 拓扑排序
4. 关键路径
五、查找
(一)查找的基本概念
(二)顺序查找法
(三)分块查找法
(四)折半查找法
(五)B树及其基本操作、B+树及其基本概念
(六)散列(Hash)表
(七)字符串模式匹配(KMP)
(八)查找算法的分析及应用
六、排序
(一)排序的基本概念
(二)插入排序
1. 直接插入排序
2. 折半插入排序
(三)起泡排序(bubble sort)
(四)简单选择排序
(五)希尔排序(shell sort)
(六)快速排序
(七)堆排序
(八)二路归并排序(merge sort)
(九)基数排序
(十)外部排序
(十一)各种内部排序算法的比较
(十二)排序算法的应用
|
2.第一讲 时间复杂度、矩阵展开
2.1时间、空间复杂度
只考虑次数,不考虑常数。也就是说考虑 n 的相关项,不考虑系数。
常见复杂度有:O(1)、O(n)、O(sqrt(n))、O(n^k)、O(logn)、O(nlogn)。
考题:2011-1、2012-1、2013-1、2014-1、2017-1、2019-1。
比较简单,直接去文件里看真题。
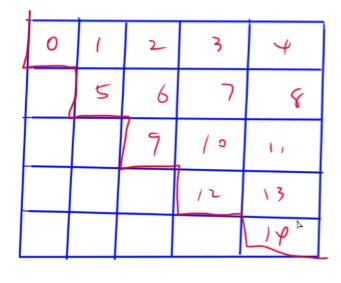
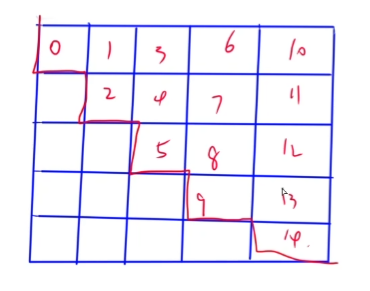
2.2特殊矩阵的存储和压缩
矩阵的按行展开、按列展开,展开后下标从0开始。
考题:2016-4、2018-3、2020-1。
难度也比较小。
按行展开(以行序为主)图示:
按列展开(以列序为主)图示:
知道了矩阵怎么压缩就可以计算它在一维数组中的下标。
对称矩阵:只需要存储上三角或者下三角;如果是上三角矩阵,那么左下方的元素就应该找它对称的位置,下三角矩阵类似。
2.3排序与进位制
3375. 成绩排序(清华考研机试题)
给定学生的成绩单,成绩单中包含每个学生的姓名和分数,请按照要求将成绩单按成绩从高到低或从低到高的顺序进行重新排列。
对于成绩相同的学生,无论以哪种顺序排列,都要按照原始成绩单中靠前的学生排列在前的规则处理。
输入格式
第一行包含整数 N,表示学生个数。
第二行包含一个整数 0或 1,表示排序规则,0 表示从高到低,1 表示从低到高。
接下来 N 行,每行描述一个学生的信息,包含一个长度不超过 10 的小写字母构成的字符串表示姓名以及一个范围在 0∼100 的整数表示分数。
输出格式
输出重新排序后的成绩单。
每行输出一个学生的姓名和成绩,用单个空格隔开。
数据范围
1≤N≤1000
输入样例1:
1
2
3
4
5
6
| 4
0
jack 70
peter 96
Tom 70
smith 67
|
输出样例1:
1
2
3
4
| peter 96
jack 70
Tom 70
smith 67
|
输入样例2:
1
2
3
4
5
6
| 4
1
jack 70
peter 96
Tom 70
smith 67
|
输出样例2:
1
2
3
4
| smith 67
jack 70
Tom 70
peter 96
|
思路:
题目要求成绩相同的学生在排序前后相对顺序不变,考察知识点:稳定排序。
可以选择algorithm库中的stable_sort() 函数,它是一个稳定排序,用法和sort()类似;
也可以自己实现稳定的排序算法,或者将下标也作为一个关键字进行sort()排序。
题目考察的另一个知识点是结构体排序。
可以在结构体内部重载运算符,或者实现一个cmp()函数。
题解一:stable_sort。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| #include <iostream>
#include <algorithm>
using namespace std;
const int N = 1005;
struct Person{
string name;
int score;
bool operator< (const Person &t) const{
return score < t.score;
}
bool operator> (const Person &t) const{
return score > t.score;
}
}p[N];
int main(){
int n,m;
cin >> n >> m;
for (int i = 0;i < n;i ++)
cin >> p[i].name >> p[i].score;
if (m == 1){
stable_sort(p,p+n);
}else{
stable_sort(p,p+n,greater<Person>());
}
for (int i = 0;i < n;i ++)
cout << p[i].name << ' ' << p[i].score << '\n';
return 0;
}
|
题解二:sort。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include <iostream>
#include <algorithm>
using namespace std;
const int N = 1005;
struct Person{
string name;
int score;
int id;
bool operator< (const Person &t) const{
if (score != t.score)
return score < t.score;
return id < t.id;
}
bool operator> (const Person &t) const{
if (score != t.score)
return score > t.score;
return id < t.id;
}
}p[N];
int main(){
int n,m;
cin >> n >> m;
for (int i = 0;i < n;i ++){
cin >> p[i].name >> p[i].score;
p[i].id = i;
}
if (m == 1){
sort(p,p+n);
}else{
sort(p,p+n,greater<Person>());
}
for (int i = 0;i < n;i ++)
cout << p[i].name << ' ' << p[i].score << '\n';
return 0;
}
|
3376. 成绩排序2(清华考研机试题)
给定学生的成绩单,成绩单中包含每个学生的学号和分数,请将成绩单按成绩从低到高的顺序重新排序。
如果学生的成绩相同,则按照学号从小到大的顺序进行排序。
输入格式
第一行包含整数 N,表示学生数量。
接下来 N 行,每行包含两个整数 p 和 q,表示一个学生的学号和成绩。
学生的学号各不相同。
输出格式
输出重新排序后的成绩单。
每行输出一个学生的学号和成绩,用单个空格隔开。
数据范围
1≤N≤100,
1≤p≤100,
0≤q≤100
输入样例:
输出样例:
思路:
双关键字排序,这里直接用pair<int,int>,也可以用结构体。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include <iostream>
#include <algorithm>
using namespace std;
const int N = 105;
typedef pair<int, int> PII;
#define fi first
#define se second
PII per[N];
int main(){
int n;
cin >> n;
int p,q;
for (int i = 0;i < n;i ++){
cin >> p >> q;
per[i] = {q,p};
}
sort(per,per+n);
for (int i = 0; i < n; i ++ )
cout << per[i].se << ' ' << per[i].fi << '\n';
return 0;
}
|
3373. 进制转换(清华考研机试题)
将一个长度最多为 30 位数字的十进制非负整数转换为二进制数输出。
输入格式
输入包含多组测试数据。
每组测试数据占一行,包含一个长度不超过 30 位的十进制非负整数。
输出格式
每组数据输出一个结果,占一行,为输入对应的二进制数。
数据范围
输入最多包含 100 组测试数据。
输入样例:
输出样例:
思路:
十进制正整数转换为二进制正整数。
除基取余法(短除法),见《日期处理与进制转换问题》,数据量一大就炸了。
c/c++进制转换方法汇总: https://blog.csdn.net/lady_killer9/article/details/87904318。
1
2
3
4
5
6
7
|
int z[40],num = 0;
do{
z[num++] = y % Q;
y /= Q;
}while (y != 0);
|
WA代码:过4个样例,数据量太大了。log2 (10^31) 约为 2^103,比unsigned long long还要大很多。
所以只能高精度了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| #include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef unsigned long long ULL;
ULL ans[31];
int main()
{
ULL a,d = 2;
while (scanf("%llu",&a) != -1){
ULL num = 0;
do{
ans[num++] = a%d;
a /= d;
}while (a != 0);
for (int i=num-1;i>=0;i--){
printf("%llu",ans[i]);
}
puts("");
}
return 0;
}
|
高精度除法模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int r = 0;
vector<int> div(vector<int> &a, int b, int &r)
{
vector<int> c;
for (int i = a.size() - 1; i >= 0; i--)
{
r = r * 10 + a[i];
c.pub(r / b);
r %= b;
}
reverse(c.begin(), c.end());
while (c.size() > 1 && c.back() == 0)
c.pop_back();
return c;
}
|
AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> div(vector<int> &a,int b){
vector<int> res;
for (int i = a.size()-1,r = 0;i >= 0;i --){
r = r*10 + a[i];
res.push_back(r / b);
r %= b;
}
reverse(res.begin(),res.end());
while (res.size() && res.back() == 0) res.pop_back();
return res;
}
int main(){
string s;
while (cin >> s){
vector<int> a;
string res;
for (int i = s.size()-1;i >= 0;i --) a.push_back(s[i] - '0');
if (s == "0") res = "0";
else{
while (a.size()){
res += to_string(a[0] % 2);
a = div(a,2);
}
reverse(res.begin(),res.end());
}
cout << res << '\n';
}
return 0;
}
|
3374. 进制转换2(清华考研机试题,有难度)
将 M 进制的数 X 转换为 N 进制的数输出。
输入格式
第一行包括两个整数:M 和 N。
第二行包含一个数 X,X 是 M 进制的数,现在要求你将 M 进制的数 X 转换成 N 进制的数输出。
输出格式
共一行,输出 X 的 N 进制表示。
数据范围
2≤N,M≤36,
X 最多包含 100 位。
在输入中,当某一位数字的值大于 10(十进制下)时,我们用大写字母 A∼Z,分别表示(十进制下的)数值 10∼35。
在输出中,当某一位数字的值大于 10(十进制下)时,我们用小写字母 a∼z,分别表示(十进制下的)数值 10∼35。
输入样例:
输出样例:
思路:
其他进制转十进制:按权展开。
1
2
3
4
5
6
7
|
int y = 0,product = 1;
while (x!=0){
y += (x%10)*product;
x /= 10;
product *= P;
}
|
秦九韶算法,秦九韶提出的一种多项式简化算法。
一般地,一元n次多项式的求值需要经过(n+1)*n/2次乘法和n次加法,而秦九韶算法只需要n次乘法和n次加法,降低了时间复杂度。( O(n^2) —> O(n) )
其他进制转十进制的过程,也就是按权展开,其实是求一个多项式的值,利用秦九韶算法提高效率。
其他a进制转其他b进制:
- 直接转换:还是短除法,不过需要用a进制除法,不是十进制除法。
- 中间借助十进制过渡。
本题 X 最多有100位,如果借助十进制转换,那么需要实现高精度加法、乘法和除法,很麻烦,所以直接用短除法。
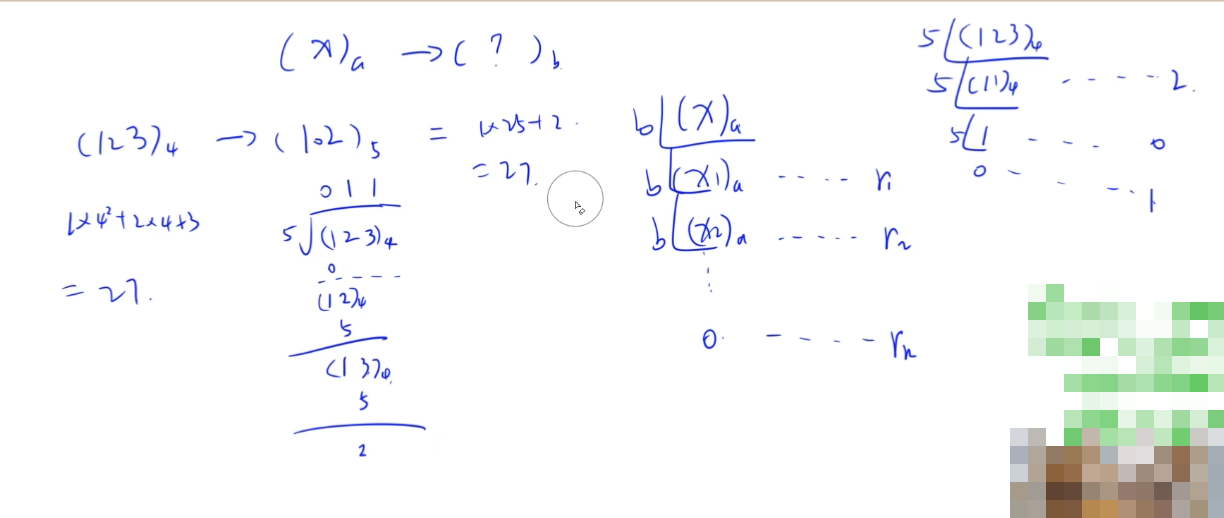
注意到做a进制除法时,为了处理/和%,我们每计算一位时需要将它和上次的余数(一共2位数)转化为十进制数(也就是高位乘上a再加上低位),再做除法。
和上一题高精度除法不太一样,本题在计算除法时就直接在被除数vector上修改,没有新开一个vector存放商。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include <iostream>
#include <algorithm>
using namespace std;
int main(){
int a,b;
string s;
vector<int> A;
cin >> a >> b >> s;
for (int i = s.size()-1;i >= 0;i --){
char c = s[i];
if (c >= 'A') A.push_back(c - 'A' + 10);
else A.push_back(c - '0');
}
string res;
if (s == "0") res = "0";
else{
while (A.size()){
int r = 0;
for (int i = A.size()-1;i >= 0;i --){
A[i] += r*a;
r = A[i] % b;
A[i] /= b;
}
while (A.size() && A.back() == 0) A.pop_back();
if (r < 10) res += to_string(r);
else res += r - 10 + 'a';
}
reverse(res.begin(),res.end());
}
cout << res << '\n';
return 0;
}
|