STL应用专题练习（二）

本专题练习参考《算法训练营—入门篇》的STL应用题单。

附上vjudge练习地址： https://vjudge.csgrandeur.cn。

补充C语言网STL专题题单： https://www.dotcpp.com/oj/train/1012/。

T1—-POJ2443

注：原题是全英文，这里机翻成中文，为保证题意理解的准确性请参考原题链接。

你被赋予了N个集合，第i个集合（由S（i）表示）具有C（i）个元素（这里的"set"与数学中定义的"set"不完全相同，一个集合可能包含两个相同的元素）。集合中的每个元素都由一个从 1 到 10000 的正数表示。现在有一些问题需要回答。查询是确定两个给定元素 i 和 j 是否同时属于至少一个集合。换句话说，您应该确定是否存在数字k（1 <= k <= N），使得元素i属于S（k），元素j也属于S（k）。
    
输入：
输入的第一行包含一个整数 N （1 <= N <= 1000），它表示集合的数量。然后按照 N 行。每个数字都以数字C（i）开头（1<= C（i）<= 10000），然后是用空格分隔的C（i）数字，然后给出集合中的元素（这些C（i）数字不必彼此不同）。N + 2 行包含一个数字 Q （1 < = Q < = 200000），表示查询数。然后按照 Q 行。每个都包含一对数字 i 和 j（1 <= i，j <= 10000，i 可能等于 j），它们描述了需要回答的元素。  
    
输出：
对于每个查询，在一行中，如果存在这样的数字k，请打印"Yes";否则请打印"No"。

考察STL：bitset。

注意到本题的数据量非常大。

C++的 bitset 在 bitset 头文件中，它是一种类似数组的结构，它的每一个元素只能是０或１，每个元素仅用１bit空间。

bitset参考博客： https://www.jb51.net/article/158006.htm。

常见用法还可以参照《算法竞赛进阶指南》。

// 这里用到的是一个bitset数组
#include <cstdio>
#include <algorithm>
#include <bitset>
using namespace std;
const int N = 10005;
bitset<1010> s[N]; // s[i]表示数i在每个集合的存在情况，1表示存在，0表示不存在

int main(){
    int n;
    scanf("%d",&n);
    
    for (int i = 1;i <= n;i ++){
        int cnt;
        scanf("%d",&cnt);
        while (cnt--){
            int x;
            scanf("%d",&x);
            s[x][i] = 1; // 数x在第i个集合出现
        }
    }
    
    int m,a,b;
    scanf("%d",&m);
    while (m--){
        scanf("%d %d",&a,&b);
        if ((s[a] & s[b]).count()) puts("Yes"); // 数a和b至少在一个集合中同时出现
        else puts("No");
    }
    return 0;
}

T2—-POJ1442

对应AcWing题目链接： https://www.acwing.com/problem/content/description/164/。（y总有讲解）

注：原题是全英文，这里机翻成中文，为保证题意理解的准确性请参考原题链接。

我们的黑匣子代表一个原始数据库。它可以保存一个整数数组，并有一个特殊的i变量。在初始时刻，黑匣子为空，i 等于 0。此黑匣子处理一系列命令（事务）。有两种类型的交易：
ADD（x）：将元素x放入黑匣子;
GET：将 i 增加 1，并在黑匣子中包含的所有整数中给出最小值 i。请记住，最小值 i是位于黑匣子元素之后的第i位的数字，按非降序排序。
让我们检查一下11个交易的可能序列：
示例1
需要制定一个有效的算法来处理给定的交易序列。ADD 和 GET 事务的最大数量：每种类型的 30000。
让我们通过两个整数数组来描述事务序列：
1. A（1）， A（2）， ...， A（M）：包含在黑匣子中的元素序列。A 值是绝对值不超过 2 000 000 000 的整数，即 M < = 30000。对于示例，我们有 A=（3， 1， -4， 2， 8， -1000， 2）。
2. u（1）， u（2）， ...， u（N）：一个序列，设置了一些元素，这些元素在第一，第二，...和 N-事务 GET。对于示例，我们有 u=（1， 2， 6， 6）。
黑匣子算法假设自然数序列 u（1）， u（2）， ...， u（N） 按非降序排序，N <= M，并且对于每个 p （1 <= p <= N）， 不等式 p <= u（p） <= M 是有效的。它源于这样一个事实，即对于我们的u序列的p元素，我们执行一个GET事务，从我们的A（1），A（2），...，A（u（p））序列中给出p最小数。
N Transaction i Black Box contents after transaction Answer 
      (elements are arranged by non-descending)   
1 ADD(3)      0 3   
2 GET         1 3                                    3 
3 ADD(1)      1 1, 3   
4 GET         2 1, 3                                 3 
5 ADD(-4)     2 -4, 1, 3   
6 ADD(2)      2 -4, 1, 2, 3   
7 ADD(8)      2 -4, 1, 2, 3, 8   
8 ADD(-1000)  2 -1000, -4, 1, 2, 3, 8   
9 GET         3 -1000, -4, 1, 2, 3, 8                1 
10 GET        4 -1000, -4, 1, 2, 3, 8                2 
11 ADD(2)     4 -1000, -4, 1, 2, 2, 3, 8   
 
输入：
输入包含（按给定顺序）：M， N， A（1）， A（2）， ...， A（M）， u（1）， u（2）， ...， u（N）。所有数字均除以空格和（或）回车符。
    
输出：
写入给定事务序列的输出黑匣子应答序列，每行一个数字。
    
样例：
7 4
3 1 -4 2 8 -1000 2
1 2 6 6
-------------------
3
3
1
2

注意读题，模拟样例。本题有一定难度。

每次ADD操作会将数按从小到大的顺序插入i之后的数中，u序列的GET操作是在插入A序列中对应编号的数后进行。

考察STL：priority_queue，对顶堆。

样例解释：

7代表下面给定7个数的数字序列，4可以理解为四次查询， 1 2 6 6为查询，第一次查询是求数字序列只有前一个数（3）时，此时的第一小的数字，即1，第二次查询是求数字序列只有前2个数（3 1）时，此时的第二小的数字,即 3，第三次查询是求数字序列只有前6个数时（3,1，-4,2,8,-1000），此时的第三小的数字，即1，第四次查询是求数字序列只有前6个数时，此时的第四小的数字。

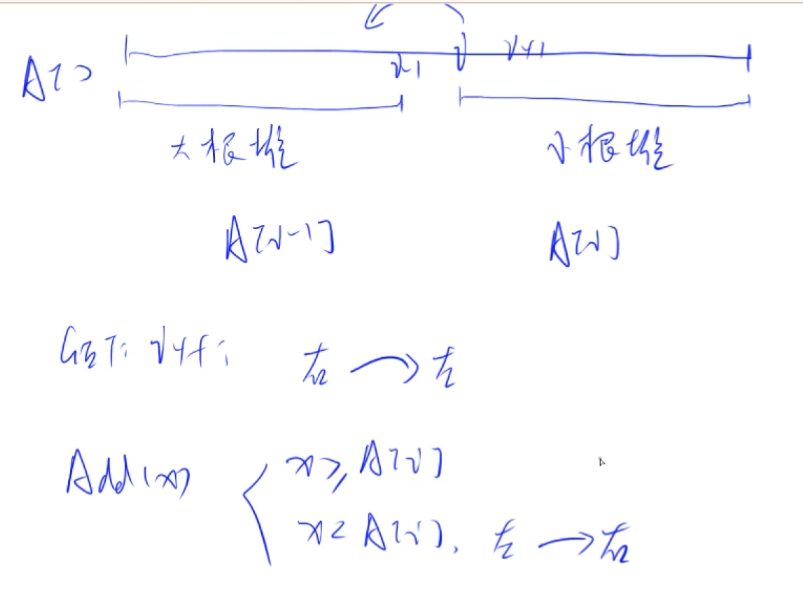
对顶堆，即一个大根堆和一个小根堆组合而成的一个数据结构，可以很方便的维护可变区间中位数。

这个玩意是可以动态维护第k大的值（比如中位数）。

对顶堆优秀博客： https://www.cnblogs.com/SGCollin/p/9673252.html。

处理动态中位数等问题，灵活运用了堆的性质，本质是维护两个堆。

大根堆Q1：维护集合中较小值的部分的最大值。

小根堆Q2：维护集合中较大值的部分的最小值。

注意到两个堆中的元素各自是单调的，两个堆间也是单调的。也就是说，Q1中的任何一个元素都不大于Q2中的任何一个元素。

y总图解：

维护对顶堆，大根堆维护的范围是0~i-1，小根堆维护的范围是i~…。这里的i表示第i次GET操作，GET操作的结果就是小根堆的堆顶。

当x > A[i]时，为维护对顶堆，左堆堆顶移到右边。

其实x = A[i]时无论加入哪个堆都行。

#include <iostream>
#include <cstdio>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 30005;
int a[N],b[N];

int main(){
    priority_queue<int> left;
    priority_queue<int,vector<int>,greater<int> > right;
    
    int m,n;
    scanf("%d %d",&m,&n);
    
    for (int i = 0;i < m;i ++) scanf("%d",&a[i]);
    for (int i = 0;i < n;i ++) scanf("%d",&b[i]);
    sort(b,b + n);
    
    int i = 0,j = 0;
    while (i < m || j < n){
        // left的元素个数 <= j
        /*cout << "i:" << i << ",j:" << j << '\n';
        cout << "left:" << left.size() << ",right:" << right.size() << '\n';*/
        // GET 操作
        while (j < n && b[j] == i){ // b[j]表示执行GET操作的时间节点
            printf("%d\n",right.top()); // GET小根堆堆顶，右堆堆顶移到左边
            left.push(right.top());
            right.pop();
            j ++;
        }
        // ADD 操作
        int x = a[i]; // 第一个数应当先插入小根堆
        if (left.empty() || x >= right.top()) right.push(x);
        else{ // 左堆堆顶移到右边，直到执行GET操作，大根堆才能向右增长一步
            left.push(x);
            right.push(left.top());
            left.pop();
        }
        i ++;
    }
    return 0;
}

T3—-POJ3481

注：原题是全英文，这里机翻成中文，为保证题意理解的准确性请参考原题链接。

新成立的巴尔干投资集团银行（BIG-Bank）在布加勒斯特开设了一个新的办事处，配备了IBM罗马尼亚提供的现代计算环境，并使用现代信息技术。像往常一样，银行的每个客户端都由一个正整数K标识，并且在到达银行进行某些服务时，他或她会收到一个正整数优先级P。银行年轻经理的发明之一震惊了服务系统的软件工程师。他们提议打破传统，有时将服务台称为优先级最低的服务台，而不是优先级最高的服务台。因此，系统将收到以下类型的请求：

0	    系统需要停止服务
1 K P	将客户机 K 添加到优先级为 P 的等待列表中
2	    以最高优先级为客户服务，并将他或她从等待名单中删除
3	    以最低的优先级为客户服务，并将他或她从等待名单中删除
您的任务是通过编写程序来实施请求的服务策略来帮助银行的软件工程师。
    
输入：
输入的每一行都包含一个可能的请求;只有最后一行包含停止请求（代码 0）。您可以假定，当请求在列表中包含新客户端（代码 1）时，同一客户端的列表中没有其他请求或具有相同的优先级。标识符 K 始终小于 10^6，优先级 P 小于 10^7。客户可能会多次到达并被送达，并且每次都可能获得不同的优先级。
    
输出：
对于每个代码为 2 或 3 的请求，程序必须在标准输出的单独一行中打印所服务客户端的标识符。如果请求在等待列表为空时到达，则程序将零 （0） 打印到输出。

考察STL：map。

有序性，这是map结构最大的优点，默认对键进行升序。

注意：输入输出数据量较大，需要scanf/printf。

#include <cstdio>
#include <algorithm>
#include <map>
using namespace std;

int main(){
    int num;
    map<int,int> hash;
    map<int,int>::iterator it;
    
    do{
        scanf("%d",&num);
        if (num == 1){
            int k,p;
            scanf("%d %d",&k,&p);
            hash[p] = k;
        }else if (num == 2){
            if (hash.empty()){
                printf("0\n");
                continue;
            }
            it = --hash.end();
            printf("%d\n",it->second);
            hash.erase(it); // 删除map中的元素，参数可以是迭代器或者键
        }else if (num == 3){
            if (hash.empty()){
                printf("0\n");
                continue;
            }
            it = hash.begin();
            printf("%d\n",it->second);
            hash.erase(it);
        }
    } while (num != 0);
    
    return 0;
}

T4—-POJ3579

注：原题是全英文，这里机翻成中文，为保证题意理解的准确性请参考原题链接。

给定 N 个数字，X1，X2，...，XN，让我们计算每对数字的差值：∣Xi - Xj∣（1 ≤ i <= j ≤ N）。我们可以通过这项工作获得C（N，2）个差异值，现在你的任务是尽快找到差异值的中位数！

注意，在这个问题中，中位数被定义为第m/2个最小数，如果差值的量m是偶数。例如，您必须在 m = 6 的情况下找到第三个最小的一个。
    
输入由多个测试用例组成。
在每个测试用例中，N 将在第一行中给出。然后给出N个数字，代表X1，X2，...，XN，（Xi ≤1，000，000，000  3 ≤N≤1，00，000）
    
对于每个测试用例，在单独的行中输出中位数。

考察STL：lower_bound/upper_bound 二分。

参考《C++竞赛语法总结（九）》。

lower_bound 的第三个参数传入一个元素x，在两个迭代器（指针）指定的部分上执行二分查找，返回指向第一个大于等于x的元素的位置的迭代器（指针）。

稍微回顾一下组合数的计算公式：

$C_{n}^{m}=\frac{A_{n}^{m}}{A_{m}^{m}}=\frac{n(n-1)(n-2) \cdots(n-m+1)}{m !}$

解题思路：首先我们要知道，n个数存在n*（n-1）/2个差值（组合数），而这个数量级就已经达到了十次方，所以我们无法直接存差值。正确的解法是二分列举差值，如果超过这个差值的组合数超过总组合数的一半，则中位数必定比该差值更大，反之则更小。

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e5+5;
int a[N],cnt,n;

bool check(int x){
    int c = 0;
    for (int i = 0;i < n;i ++){
        c += n - (lower_bound(a,a + n,a[i] + x) - a);
    }
    return c > cnt;
} 

int main(){
    while (scanf("%d",&n) != EOF){
        cnt = n*(n-1) / 4; // 所有组合总数c(n,2)的一半
        for (int i = 0;i < n;i ++) scanf("%d",&a[i]);
        
        sort(a,a + n);
        int l = 0,r = a[n-1] - a[0]; // 二分枚举差异值m
        while (l < r){ // 二分模板
            int mid = l + r + 1 >> 1;
            if (check(mid)) l = mid;
            else r = mid - 1; // 如果差异值 >= 当前差异值m的组合数不足一半说明答案在左边
        }
        cout << l << '\n';
    }
    return 0;
}