grant's Blog

记录生活中的点点滴滴

算法提高课笔记（一）

发表于 更新于 分类于 ，   阅读次数： Valine：
本文字数： 7.6k 阅读时长 ≈ 7 分钟

一：动态规划

提高课介绍：基础课主要讲了常见算法模型和相应的模板，题目都是裸题；提高课会注重提高深度，反复磨练一种题型，提高熟练度。

专门练习题型可以看提高课目录，也可以打一下AC Saber的训练模式。

1.1：数字三角形模型

数字三角形模板题见：算法基础课笔记（二四）。

1015.摘花生

蓝桥杯学习总结（十一）中有这道题的题解。

image-20211006192213314

下面直接给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int t;
const int N = 105;
int a[N][N],f[N];

int main(){
	cin >> t;
	int r,c;
	while (t--){
		cin >> r >> c;
		memset(f,0,sizeof f);// 每次处理一组数据必须重置f
		for (int i = 1;i <= r;i ++)
			for (int j = 1;j <= c;j ++){
				cin >> a[i][j];
				f[j] = max(f[j-1],f[j]) + a[i][j];
			}		
		cout << f[c] << '\n';
	}
	return 0;
}

摘花生必须保证第一行和第一列不能由网格外边界转移而来，但是全局变量初始化为0，f[0][...]和f[...][0]都为0，求Max不会转移到第一行第一列。所以不需要额外处理。

由于多组样例，而二维数组解法由于f[0][...]和f[...][0]都为0，所以没有问题。对于一维数组，上一样例的f数组需要清零，否则影响结果。

这相当于二维数组有个在地图外的一行一列的缓冲区，在计算时不会用到，而一维数组没有缓冲区，就需要每次计算前将数组置零。

1018. 最低通行费

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
一个商人穿过一个 N×N 的正方形的网格，去参加一个非常重要的商务活动。
他要从网格的左上角进，右下角出。
每穿越中间 1 个小方格，都要花费 1 个单位时间。
商人必须在 (2N−1) 个单位时间穿越出去。
而在经过中间的每个小方格时，都需要缴纳一定的费用。
这个商人期望在规定时间内用最少费用穿越出去。
请问至少需要多少费用？
注意：不能对角穿越各个小方格（即，只能向上下左右四个方向移动且不能离开网格）。

输入格式
第一行是一个整数，表示正方形的宽度 N。
后面 N 行，每行 N 个不大于 100 的正整数，为网格上每个小方格的费用。

输出格式
输出一个整数，表示至少需要的费用。

数据范围
1≤N≤100
输入样例：
5
1  4  6  8  10
2  5  7  15 17
6  8  9  18 20
10 11 12 19 21
20 23 25 29 33
输出样例：
109
样例解释
样例中，最小值为 109=1+2+5+7+9+12+19+21+33。

先计算一下最少需要的单位时间。

首先进去消耗1个单位时间，然后往右走到头，再往下走到头，总时间为：1+2*(N-1) = 2*N-1。

所以商人不能走回头路，这题就和摘花生差不多了。

区别在于：摘花生求最大值，本题求最小值，需要将网格除起点外的点初始化INF。

需要先把所有状态初始化为正无穷，初始化状态的起点（dp求最小值必须要的步骤）。

算法1：DP。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 105,INF = 0x3f3f3f3f;
int a[N][N],f[N][N];
int n;

int main(){
    cin >> n;
    
    memset(f,0x3f,sizeof f);
    for (int i = 1;i <= n;i ++)
        for (int j = 1;j <= n;j ++){
            cin >> a[i][j];
            if (i == 1 && j == 1) f[i][j] = a[i][j];
            else{
                f[i][j] = min(f[i-1][j],f[i][j-1]) + a[i][j];
            }
        }
    cout << f[n][n] << '\n';
    return 0;
}

注意点：

f[1][1]是起点，必须初始化为a[1][1]；

必须保证第一行和第一列不能由网格外边界转移而来，y总在else中用了2个if来判断，这里直接令整个 f 数组置INF，因为坐标从1开始算，而f[0][...]和f[...][0]都为INF，求Min所以它们不可能转移到f[1][...]和f[...][1]。

算法2：记忆化搜索。

参考题解： https://www.acwing.com/solution/content/51101/。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 105,INF = 0x3f3f3f3f;
int f[N][N],a[N][N];

int dp(int x,int y){
    if (f[x][y] >= 0) return f[x][y];// f[x][y] != -1表示已经搜索过，直接返回结果
    if (x == 1 && y == 1) return a[1][1];
    if (x < 1 || y < 1) return INF;
    
    int res = INF;
    res = min(res,dp(x-1,y));
    res = min(res,dp(x,y-1));
    return f[x][y] = res + a[x][y]; // 长见识了，函数返回赋值表达式
    // 这样写等价于 f[x][y] = res + a[x][y]; return f[x][y];
}

int main(){
    int n;cin >> n;
    for (int i = 1;i <= n;i ++)
        for (int j = 1;j <= n;j ++) cin >> a[i][j];
        
    memset(f,-1,sizeof f);// f[x][y] == -1表示还没有搜索过
    cout << dp(n,n) << '\n';
    return 0;
}

以上两道题都需要处理边界问题，处理方法与都和模型题数字三角形相似，正向要处理边界，逆向不要。对应数字三角形的2种题解。

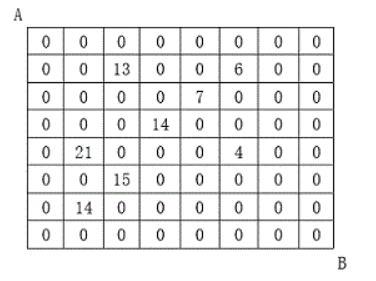
1027. 方格取数

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

image-20211007101331570

某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
输入格式
第一行为一个整数N，表示 N×N 的方格图。
接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。
行和列编号从 1 开始。
一行“0 0 0”表示结束。

输出格式
输出一个整数，表示两条路径上取得的最大的和。

数据范围
N≤10
输入样例：
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出样例：
67

本题和摘花生的区别就是多走了一次，会改变方格中的数。

注意：这题不能走两次，每次取最大值再相加。

为什么？

因为第一遍的最优解可能有非常多种方案，不确定选择哪一种，而第一遍会影响第二遍的最优解。

分开两次走（贪心）：第一次走到(n, n)求出最大值并记录路径令路径上点收益为0后再走一次。
第一次走为局部最优并且也对第二次走造成了影响，第二次走是在第一次影响下所能走的局部最优，不具备“无后效性”，因此分开两次走并不是全局最优解。

所以正确的做法是同时进行两条路线求解。这道题目其实属于多线程DP。

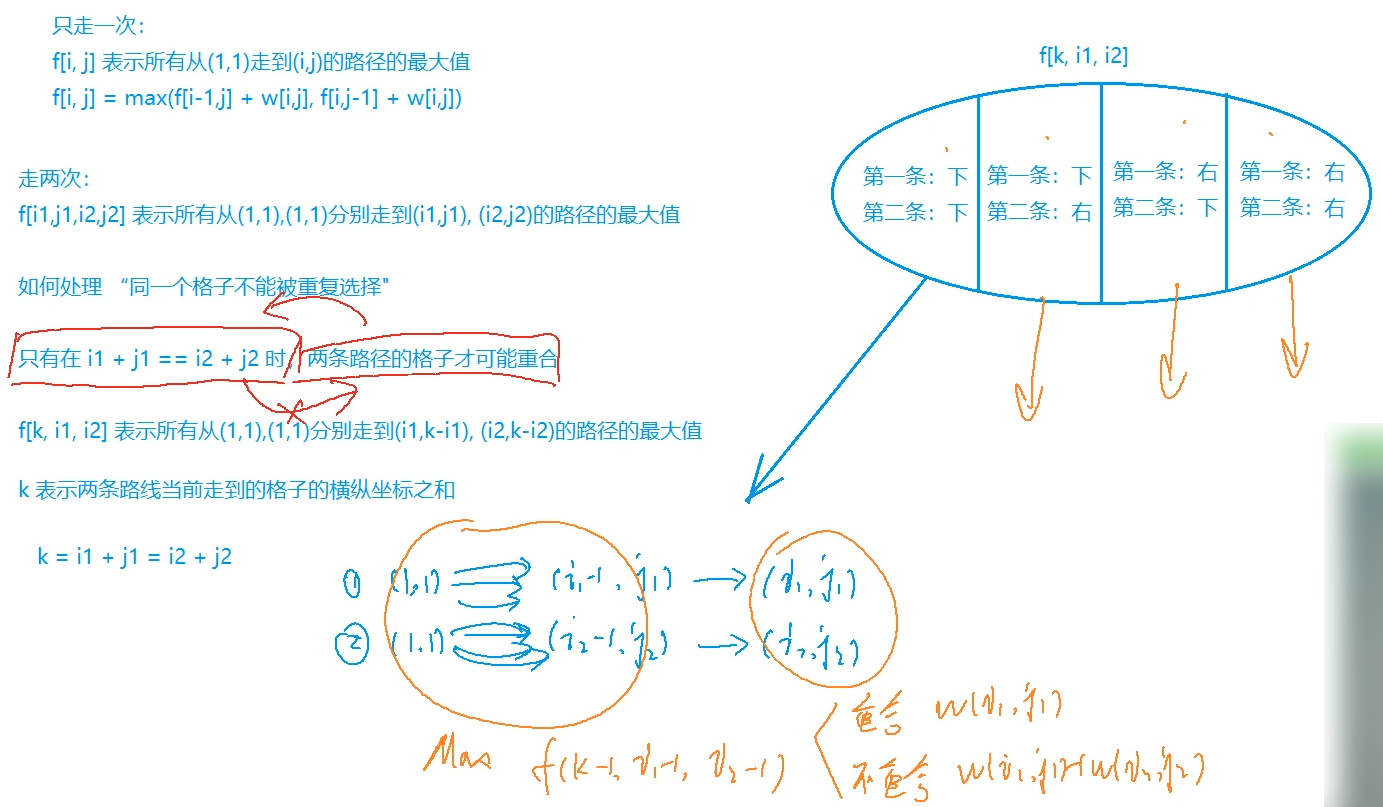
状态计算：两条路线同时走，总步数相等（等价于i1+j1 == i2+j2），这样可以减少一个维度。

因为只能向下走和向右走，所以不管哪种走法，它们的总步数都是一样的。只有i1+j1 == i2+j2才有可能发生两条路线走到同一个格子。

两条路线的最大值需要同时考虑，不能先看一条路线的最大值，再看另一个。

闫氏DP分析法：

image-20211007123938568

本题和摘花生的边界情况类似，由于状态计算是求Max，且网格内都是正整数，边界为0，求Max不会转移到第一行第一列。所以不需要额外处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 15;
int w[N][N],f[N*2][N][N];

int main(){
    int n,a,b,c;
    cin >> n;
    while (cin >> a >> b >> c && a || b || c){
        w[a][b] = c;
    }
    
    for (int k = 2;k <= n*2;k++)
        for (int i1 = 1;i1 <= n;i1 ++)
            for (int i2 = 1;i2 <= n;i2 ++){
                int j1 = k - i1,j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n){ // 纵坐标不能出界
                    int &x = f[k][i1][i2];// 简化代码
                    int t = w[i1][j1];
                    if (i1 != i2) t += w[i2][j2]; // 不重合，两个都要加上
                    x = max(x,f[k-1][i1-1][i2-1] + t);
                    x = max(x,f[k-1][i1-1][i2] + t);
                    x = max(x,f[k-1][i1][i2-1] + t);
                    x = max(x,f[k-1][i1][i2] + t);
                }
            }
    cout << f[n*2][n][n] << '\n';
    return 0;
}

方格取数是摘花生走2遍，还有摘花生终极版，k取方格数，走k遍，用最小费用流解决，有兴趣可以尝试。

DP其实是图论的子集，大多数DP可以转化为最短路求解。拓扑图的最短路也可以转化为DP求解。

275. 传纸条

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。
一次素质拓展活动中，班上同学安排坐成一个 m 行 n 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。
幸运的是，他们可以通过传纸条来进行交流。
纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 (1,1)，小轩坐在矩阵的右下角，坐标 (m,n)。
从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。 
在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。
班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙，反之亦然。 
还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 0 表示），可以用一个 0∼100 的自然数来表示，数越大表示越好心。
小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。
现在，请你帮助小渊和小轩找到这样的两条路径。

输入格式
第一行有 2 个用空格隔开的整数 m 和 n，表示学生矩阵有 m 行 n 列。
接下来的 m 行是一个 m×n 的矩阵，矩阵中第 i 行 j 列的整数表示坐在第 i 行 j 列的学生的好心程度，每行的 n 个整数之间用空格隔开。

输出格式
输出一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

数据范围
1≤n,m≤50
输入样例：
3 3
0 3 9
2 8 5
5 7 0
输出样例：
34

本题可以转化为方格取数来求解。

从右下角回传给左上角，其实就等价于与从左上角传给右下角。所以本题也就是传了2次纸条，也不能相交，剩下的就是方格取数问题了，基本完全等价。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 55;
int w[N][N],f[N*2][N][N];

int main(){
    int m,n;
    cin >> m >> n;
    for (int i = 1;i <= m;i ++)
        for (int j = 1;j <= n;j ++) cin >> w[i][j];
        
    for (int k = 2;k <= n+m;k++)
        for (int i1 = 1;i1 <= m;i1 ++)
            for (int i2 = 1;i2 <= m;i2 ++){
                int j1 = k - i1,j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n){ // 纵坐标不能出界
                    int &x = f[k][i1][i2];// 简化代码
                    int t = w[i1][j1];
                    if (i1 != i2) t += w[i2][j2]; // 不重合，两个都要加上
                    x = max(x,f[k-1][i1-1][i2-1] + t);
                    x = max(x,f[k-1][i1-1][i2] + t);
                    x = max(x,f[k-1][i1][i2-1] + t);
                    x = max(x,f[k-1][i1][i2] + t);
                }
            }
    cout << f[n+m][m][m] << '\n';
    return 0;
}

优质题解： https://www.acwing.com/solution/content/12389/。

经过证明：两条路线相交的方案肯定不是最优解。

另一份题解： https://www.acwing.com/solution/content/51293/。

洛谷聚聚的二维空间优化题解： https://www.luogu.com.cn/blog/oiertan-zl/solution-p1006。

二维就是对三维的等价变形！！！。

看清楚当前的f[i1][i2]等价于f[k][i1][i2]还是f[k-1][i1][i2]，这点很重要！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 55;
int w[N][N],f[N][N];

int main(){
    int m,n;
    cin >> m >> n;
    for (int i = 1;i <= m;i ++)
        for (int j = 1;j <= n;j ++) cin >> w[i][j];
        
    for (int k = 2;k <= n+m;++ k)
        for (int i1 = m;i1 >= 1;-- i1)
            for (int i2 = m;i2 >= 1;-- i2){
                int j1 = k - i1,j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n){ // 纵坐标不能出界
                    int &x = f[i1][i2];// 简化代码
                    int t = w[i1][j1];
                    if (i1 != i2) t += w[i2][j2]; // 不重合，两个都要加上
                    x = max(x,f[i1-1][i2-1]);
                    x = max(x,f[i1-1][i2]);
                    x = max(x,f[i1][i2-1]);
                    x = max(x,f[i1][i2]);
                    x += t;
                }
            }
    cout << f[m][m] << '\n';
    return 0;
}

记忆化搜索：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 55;
int w[N][N],f[N*2][N][N];

int dp(int k,int x,int y){
    if (f[k][x][y] != -1) return f[k][x][y]; // 之前搜索过直接返回答案
    if (x == 1 && y == 1) return w[1][1]; // 递归边界
    if (x < 1 || y < 1 || k-x < 1 || k-y < 1) return -1;
    
    int t = w[x][k-x];
    int &res = f[k][x][y];
    if (x != y) t += w[y][k-y];
    res = max(res,dp(k-1,x,y));
    res = max(res,dp(k-1,x-1,y));
    res = max(res,dp(k-1,x-1,y-1));
    res = max(res,dp(k-1,x,y-1));
    return res = res + t;
}

int main(){
    int m,n;
    cin >> m >> n;
    
    for (int i = 1;i <= m;++ i)
        for (int j = 1;j <= n;++ j) cin >> w[i][j];
    
    memset(f,-1,sizeof f);
    cout << dp(m+n,m,m) << '\n';
    return 0;
}
坚持原创技术分享，您的支持将鼓励我继续创作！