考研算法辅导课笔记（十八）

2021-1

2021年408真题地址： https://www.doc88.com/p-66216037546804.html?r=1。

答案选D。

B选项操作错在没有考虑循环链表只有一个结点的情况，此时p == q，需要更新尾指针。

2021-2

答案选D。

栈和队列的结合，手动模拟就行。

2021-3

二维数组按行优先存储，设数组的行大小为L个单位，A[0][0]和A[3][3]中间间隔3L+2个单位。由于存储地址取的是单位的左端，所以3L+2+1 = 220 - 110，解得L = 39。

A[3][3]和A[5][5]中间间隔2L+1个单位。由于存储地址取的是单位的左端，所以2L+1+1 = x - 220，解得x = 300。

答案选B。

2021-4

回顾森林F与二叉树T的转换。

也就是左孩子右兄弟表示法。

根据前序和中序遍历构造二叉树。

答案选C。

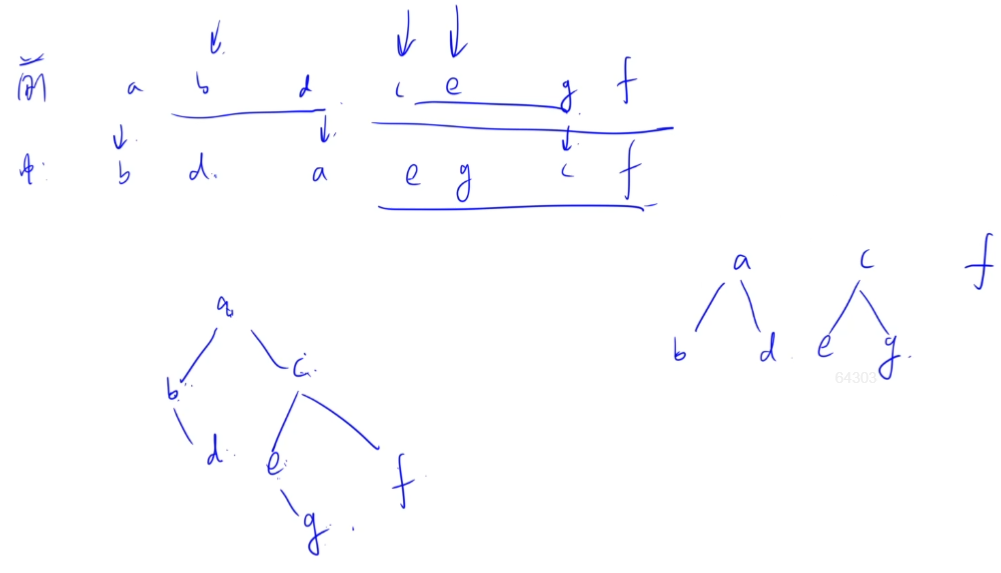
2021-5

WPL可以按照定义计算，也可以计算所有非叶节点的权值之和。

答案选B。

2021-6

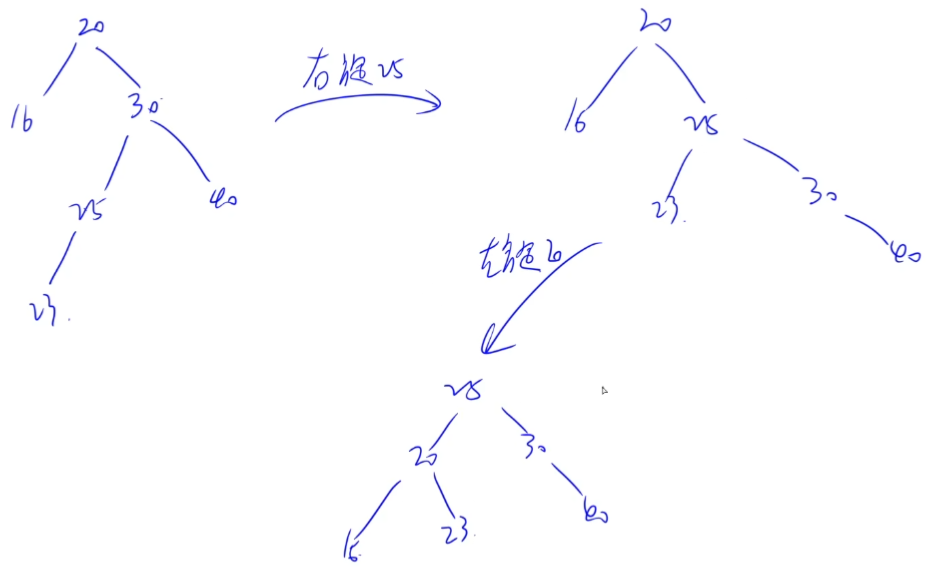
考察AVL的插入操作。（不改变中序序列）

每次考虑最小不平衡子树进行旋转操作，可能要进行多次旋转。

对应从20到23的这条路径，需要进行RL旋转。

答案选D。

2021-7

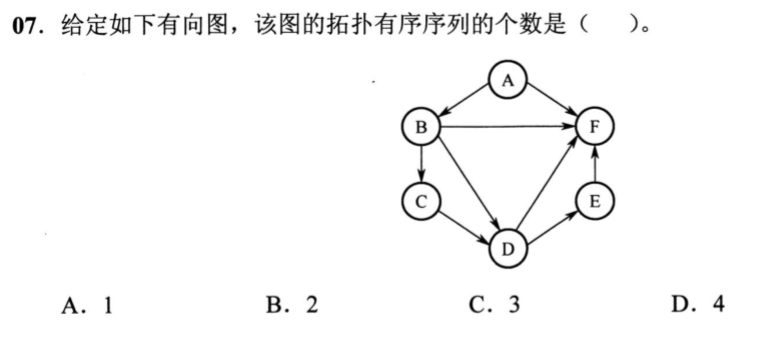
答案选A。

每一步入度为0的节点都只有一个。

2021-8

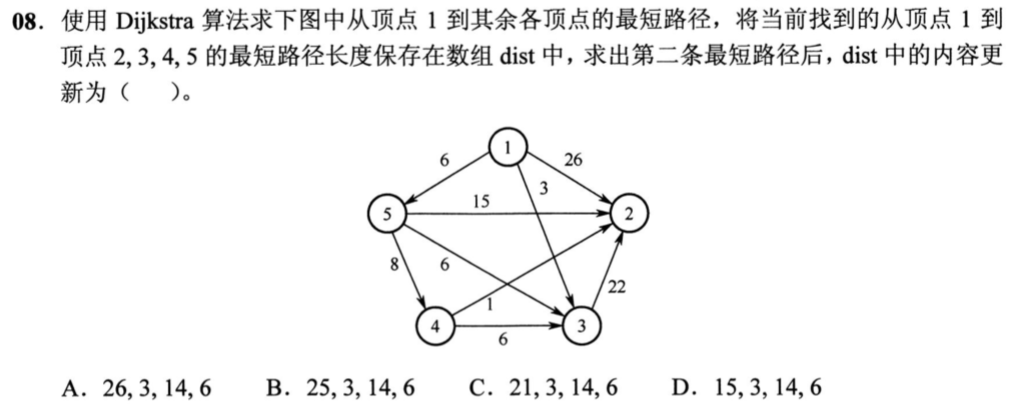
Dijkstra算法，每一轮边松弛操作会将一个除起点外的其他点加入集合，并用它更新dist数组。

求出第二条最短路径，也就是执行了两轮边松弛操作，找到了两个点，3号和5号。此时dist[2]应该等于21。

答案选C。

2021-9

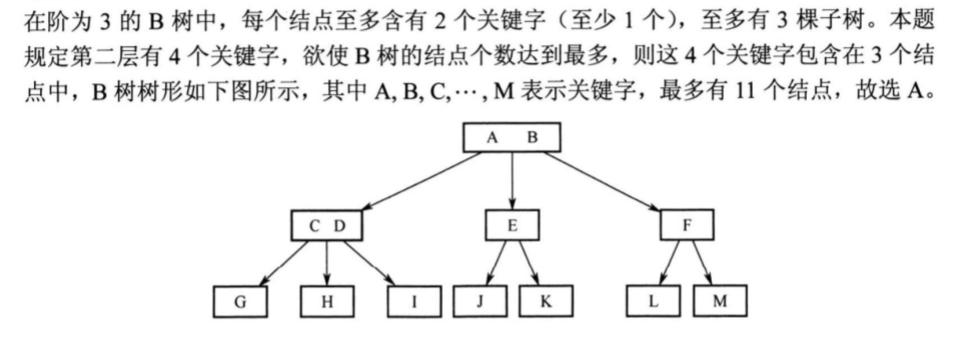
3阶B树，每个节点最多有2个关键字，3个孩子。非根节点至少有ceil(m/2)-1个关键字。

注意4个关键字的分配方式有多种，选择总节点个数最多的方式。

根节点的关键字也有两种情况。

答案选A。（容易做错）

2021-10

手动模拟基数排序。

答案选C。按照低位优先排序，从个位开始排序。

2021-11

模拟大根堆的插入操作。（前面堆排序中没有涉及）

每次往大根堆中插入一个元素，加到堆底，执行一次up操作。

答案选B。

2021-41

图论新知识点：欧拉路径。

概念补充与拓展知识：

如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径(Euler path)。

如果一个回路是欧拉路径，则称为欧拉回路(Euler circuit)。

具有欧拉回路的图称为欧拉图（简称E图）。具有欧拉路径但不具有欧拉回路的图称为半欧拉图。

欧拉回路是数学家欧拉在研究著名的德国哥尼斯堡(Koenigsberg)七桥问题时发现的。

无向图存在欧拉回路的充要条件

一个无向图存在欧拉回路，当且仅当该图所有顶点度数都为偶数,且该图是连通图。

有向图存在欧拉回路的充要条件

一个有向图存在欧拉回路，所有顶点的入度等于出度且该图是连通图。

---

一个无向连通图存在欧拉路径的充要条件是度数为奇数的点的个数为0或2。（题干中也有）

核心思路就是求度数为奇数的点的个数。

参考答案：

2021-42

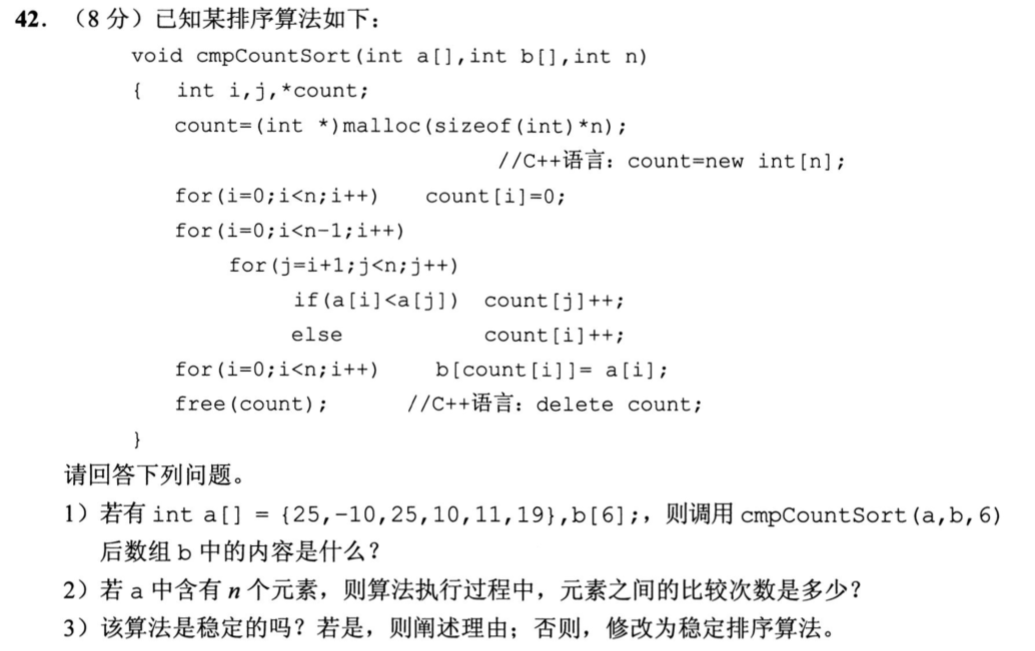
（1）排序算法执行完后，b数组中的内容就是从小到大排好序的a数组-10,...,25,25。

（2）n*(n-1)/2次。

（3）不是稳定的。加一个等号就行。

参考答案：

2021的两道算法题都是送分题。

第十三讲 红黑树和并查集

1. 红黑树
   1.1 定义

    (1) 结点是红色或黑色。
    (2) 根结点是黑色。
    (3) 所有叶子都是黑色。（叶子是NIL结点）
    (4) 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）
    (5) 从任一节结点其每个叶子的所有路径都包含相同数目的黑色结点。
   

   1.2 性质

    从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。
   

   1.3 平衡操作

    1.3.1 插入
        1.3.1.1 被插入的节点是根节点。
            直接把此节点涂为黑色。
        1.3.1.2 被插入的节点的父节点是黑色。
            什么也不需要做。
        1.3.1.3 被插入的节点的父节点是红色。
            [1] 当前节点的祖父节点的另一个子节点（叔叔节点）也是红色。
                (1) 将“父节点”设为黑色。
                (2) 将“叔叔节点”设为黑色。
                (3) 将“祖父节点”设为“红色”。
                (4) 将“祖父节点”设为“当前节点”(红色节点)；即，之后继续对“当前节点”进行操作。
            [2] 叔叔节点是黑色，且当前节点是其父节点的右孩子
                (1) 将“父节点”作为“新的当前节点”。
                (2) 以“新的当前节点”为支点进行左旋。
            [3] 叔叔节点是黑色，且当前节点是其父节点的左孩子
                (1) 将“父节点”设为“黑色”。
                (2) 将“祖父节点”设为“红色”。
                (3) 以“祖父节点”为支点进行右旋。
    1.3.2 删除
        1.3.2.1 x指向一个"红+黑"节点。
            将x设为一个"黑"节点即可。
        1.3.2.2 x指向根。
            将x设为一个"黑"节点即可。
        1.3.2.3 
            [1] x的兄弟节点是红色。
                (1) 将x的兄弟节点设为“黑色”。
                (2) 将x的父节点设为“红色”。
                (3) 对x的父节点进行左旋。
                (4) 左旋后，重新设置x的兄弟节点。
            [2] x的兄弟节点是黑色，x的兄弟节点的两个孩子都是黑色。
                (1) 将x的兄弟节点设为“红色”。
                (2) 设置“x的父节点”为“新的x节点”。
            [3] x的兄弟节点是黑色；x的兄弟节点的左孩子是红色，右孩子是黑色的。
                (1) 将x兄弟节点的左孩子设为“黑色”。
                (2) 将x兄弟节点设为“红色”。
                (3) 对x的兄弟节点进行右旋。
                (4) 右旋后，重新设置x的兄弟节点。
            [4] x的兄弟节点是黑色；x的兄弟节点的右孩子是红色的，x的兄弟节点的左孩子任意颜色。
                (1) 将x父节点颜色 赋值给 x的兄弟节点。
                (2) 将x父节点设为“黑色”。
                (3) 将x兄弟节点的右子节设为“黑色”。
                (4) 对x的父节点进行左旋。
   

2. 并查集
   2.1 定义

    用森林维护集合关系，支持合并、查询等操作。
   

   2.2 优化

    (1) 路径压缩
    (2) 按秩合并
   

---

红黑树代码很长很复杂，以大题形式考察可能性不大。

并查集比较简单。

红黑树知识这里就跳过了。（不考408嘿嘿，要考408的同学看看y总视频）

并查集知识参考《并查集详解》以及《算法基础课笔记（十一）》。

---

模板链接：https://www.acwing.com/blog/content/404/

并查集 —— 模板题:AcWing 836. 合并集合, AcWing 837. 连通块中点的数量

(1)朴素并查集：

int p[N]; //存储每个点的祖宗节点

// 返回x的祖宗节点
int find(int x)// 路径压缩
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;

// 合并a和b所在的两个集合：
p[find(a)] = find(b);  // 不要写成p[a] = b;

(2)维护size的并查集：

int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

// 返回x的祖宗节点
int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
    p[i] = i;
    size[i] = 1;
}

// 合并a和b所在的两个集合：
a = find(a),b = find(b);// 必须用变量存一下find，否则下面会改变find导致bug
if (find(a) != find(b)){// a,b祖宗不同才需要合并，否则已经合并了
    p[a] = b;
    Size[b] += Size[a];
}

(3)维护到祖宗节点距离的并查集：

int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

// 返回x的祖宗节点
int find(int x)
{
    if (p[x] != x)
    {
        int u = find(p[x]);
        d[x] += d[p[x]];
        p[x] = u;
    }
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
    p[i] = i;
    d[i] = 0;
}

// 合并a和b所在的两个集合：
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

并查集的两种优化：路径压缩和按秩合并。

最坏情况时间复杂度为：O(m*logn)。n是集合大小，m是查询次数。

在很大范围内并查集的单次查询耗时近似为O(1)。

启发式合并（按秩合并）：

如果我们将一棵点数与深度都较小的集合树连接到一棵更大的集合树下，显然相比于另一种连接方案，接下来执行查找操作的用时更小（也会带来更优的最坏时间复杂度）。

当然，我们不总能遇到恰好如上所述的集合————点数与深度都更小。鉴于点数与深度这两个特征都很容易维护，我们常常从中择一，作为估价函数。

按秩合并对于路径压缩后的并查集提升不会太明显。

acwing.836. 合并集合

一共有 n 个数，编号是 1∼n，最开始每个数各自在一个集合中。
现在要进行 m 个操作，操作共有两种：
M a b，将编号为 a 和 b 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
Q a b，询问编号为 a 和 b 的两个数是否在同一个集合中；
    
输入格式
第一行输入整数 n 和 m。
接下来 m 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式
对于每个询问指令 Q a b，都要输出一个结果，如果 a 和 b 在同一集合内，则输出 Yes，否则输出 No。
每个结果占一行。

数据范围
1≤n,m≤10^5
输入样例：
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例：
Yes
No
Yes

代码：（路径压缩+按秩合并版本）

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5+5;
int p[N],r[N],n,m; // p是并查集数组，r维护树根的树高

int find(int x){ // 路径压缩的查询
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void merge(int a,int b){ // 按秩合并两个集合
    a = find(a),b = find(b);
    if (a == b) return; // 同一集合不用合并
    else if (r[a] > r[b]) p[b] = a; // 矮树插入高树，不影响高树高度
    else{
        p[a] = b;
        if (r[a] == r[b]) r[b] ++; // 两树同高，树根高度++
    }
}

int main(){
    cin >> n >> m;
    
    for (int i = 1;i <= n;i ++) p[i] = i; // 初始化并查集
    
    char op;int a,b;
    while (m--){
        cin >> op >> a >> b;
        if (op == 'M') merge(a,b);
        else cout << (find(a) == find(b) ? "Yes\n" : "No\n");
    }
    
    return 0;
}

---

数据结构的笔试部分就到这里结束。